Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsia_8.doc

Скачиваний:

Добавлен:

01.03.2025

Размер:

4.96 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

121

^⁸Четырехмерный мир (пространство-время)

В пространственных координатах положение каждой точки задается тройкой чисел (координатами точки). Расстояние между двумя бесконечно близкими точками многообразия – важная характеристика пространства – определяет основные геометрические характеристики: длины векторов, углы между ними, расстояния, площади и объемы.

В мире, в котором мы живем, с большой точностью справедлива геометрия Евклида. В декартовых координатах, которые выделены своей простотой:

(теорема Пифагора для диагонали трехмерного прямоугольного параллелепипеда), не зависит от выбора системы координат, т. е. – инвариант.

Вспомним общее определение интервала:

координаты события 1 - ;

координаты события 2 - .

Введем обозначение интервала - или .

Основным свойством интервала между событиями является его инвариантность относительно перехода от одной ИСО к другой ИСО.

Инвариантом является также расстояние между точками:

Нельзя представить себе четырехмерное пространство наглядно, но это и не нужно. Будем просто переносить на n-мерное пространство соотношения, полученные для трехмерного пространства.

4-мерное пространство: .

Расстояние между бесконечно близкими точками:

Расстояние между точками (инвариант):

Можно обозначить: .

Тогда для n-мерного пространства:

Расстояние между точками:

Итак, задав определенные для данного типа пространства инварианты (в нашем случае евклидова пространства инвариантом является расстояние между точками), можно построить геометрические соотношения для пространства любой размерности.

Итак, 4-мерный пространственно-временной континуум, точками которого являются события, называют миром Минковского.

Немецкий ученый H. Minkowski – В 1907-1908 г. объединил трехмерное пространство и время. Точки в этом 4-мерном пространстве обозначают события в СТО.

Последовательность событий, происходящих с материальной точкой (частицей), образует в мире Минковского некоторую кривую, называемую мировой линией частицы.

Основные выводы

1) 4-мерный пространственно-временной континуум, точками которого являются события, называют миром Минковского.

2) «Расстояние» между точками в мире Минковского – это интервал СТО, он инвариантен относительно преобразований Лоренца.

3) Вместо обычных 3-мерных векторов (и тензоров) в мире Минковского мы строим 4-мерные векторы и (4-мерные тензоры) таким образом, чтобы они обладали инвариантностью по отношению к преобразованиям Лоренца.

4) Построение этих 4-мерных векторов не всегда осуществляется просто. Обычно 3-мерный вектор образует пространственную часть искомого 4-мерного вектора, а четвертая (временная-ударение на а) компонента часто имеет неожиданное, но при ближайшем рассмотрении вполне естественное выражение, которое в нерелятивистском приближении переходит в классическое.

5) Последовательность происходящих с частицей (материальной точкой, телом) событий образует в мире Минковского некоторую кривую, называемую мировой линией частицы.

Классификация интервалов в СТО

(данный материал является дополнительным)

РИС. 6-4

Если взять две мировые точки, то квадрат интервала между ними:

Пусть событие 1 наступило в точке , . Любые события, наступившие до и после события 1, изображаются точками на плоскости .

«Расстояние» (интервал) от события 1 до любого события на плоскости мира Минковского: .

На прямых всегда .

Такой интервал называется светоподобным.

Светоподобным называется интервал между событиями, расстояние между которыми на псевдоевклидовой плоскости равно нулю.

Светоподобные прямые выделяют на плоскости четыре квадранта:

. Для всех событий этого квадранта ; значит, все эти события происходят позже события 1 и никаким выбором системы отсчета это изменить нельзя. Следовательно, интервал между событием 1 и любым событием в квадранте I – времени - подобный, и квадрант I – это область абсолютного будущего. Легко убедиться, что последовательность событий в квадранте I не зависит от выбора системы отсчета.

Будущее – это все события, на которые, вообще говоря, может повлиять, то, что мы делаем здесь и сейчас. Эти события находятся в световом конусе будущего.

Примечание

- это уравнение, описывающее распространение света в 4-мерном пространстве, с точки зрения математики это есть уравнение конуса, который обычно называют световым конусом.

, но для всех событий этого квадранта , т. е. все события в этом квадранте произошли раньше события 1. Это область абсолютного прошлого.

Прошлое – это множество всех событий, которые, вообще говоря, могли бы оказать воздействие на то, что происходит здесь и сейчас.

Итак, внутренние полости конуса соответствуют областям «абсолютного будущего» и «абсолютного прошлого». Между событиями, лежащими на внутренней полости световых конусов, может существовать причинная связь.

В квадрантах III и IV , такой интервал называют пространственно-подобным: все события в квадрантах III и IV происходят в точках пространства, не совпадающих с точкой события 1; изменить это путем соответствующего выбора системы отсчета невозможно. Однако можно найти такие системы отсчета, в которых события, находящиеся в квадрантах III и IV, произошли бы раньше, позже или одновременно с событием 1, поскольку понятия «раньше», «позже» или «одновременно» для этих событий относительны, ибо эти события не могут быть связаны с событием 1 причинной связью.

Классификация интервалов

Квадранты	Соотношения между координатами и временем для двух событий	Тип интервала	Характер связи между событиями
I II		Времени-подобный	Может быть причинно-следственная связь
III IV		Пространственно-подобный	Нет причинной связи
Биссектриса		Свето-подобный	События могут быть связаны световым сигналом

На евклидовой плоскости геометрическим местом точек, равноудаленных от

н ачала координат, является окружность .

РИС.6-5 РИС.6-6

На псевдоевклидовой плоскости квадрат «расстояния» от начала координат до равноудаленных от него точек: - это уравнение гиперболы.

Световой конус – это асимптоты гипербол.

О парадоксе близнецов (часов)

Напомнание!

При , и угол поворота . Свет распространяется по биссектрисе.

РИС. 4п-6

РИС. 6-8

Исходно близнецы находятся в точке .

Путешественник совершает движение на участке , затем на участке - движение равномерное и прямолинейное везде кроме небольших участков вблизи точек , где он совершает разгон, поворот и торможение, т.е. движется с ускорением. Поскольку мы ничего не знаем о движении с ускорением (не знаем, как ускорение влияет на ход часов), будем полагать, что эти участки малы по сравнению с и .

Сделаем важное определение.

П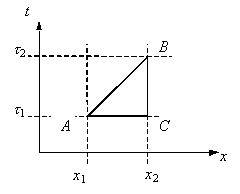 севдопифагорова теорема

РИС. 6-1

Теперь вспомним определение интервала между точками А и В, . Этот результат получен в соответствии с определением интервала в СТО, он похож на теорему Пифагора, но противоречит ей.

Итак, длина мировой линии «путешественника» согласно псевдопифагоровой теореме:

-------------------------------

Длина мировой линии «домоседа»:

- больше, чем длина мировой линии «путешественника».

Значит, по собственному времени «путешественник» прожил меньше, чем «домосед».

Парадоксальным является утверждение о том, что с точки зрения «путешественника» он является «домоседом», а «домосед» - «путешественником».

Еще раз о парадоксе близнецов с применением некоторых формул

(дополнительный материал)

Имеем двое синхронизованных часов и .

В момент часы и находятся в начале отсчета (точка ). Пусть покоятся в точке , а совершают следующее движение: ускоряются на участке , движутся равномерно со скоростью на участке , тормозятся той же силой на отрезке , движутся равномерно и прямолинейно на отрезке , затем та же сила тормозит часы, и они приходят в исходную точку .

РИС. 6-9

При бесконечно большой внешней силе время, необходимое для ускорения часов на участке и торможения в точке поворота , равно нулю. Значит, время, необходимое для путешествия, равно удвоенному времени пролета отрезка с постоянной скоростью .

По часам от момента «отъезда» до момента «приезда» прошло время , а по часам - .

По часам в неподвижной системе K:

С точки зрения наблюдателя, движущегося вместе с часами : часы покоятся, а часы сначала удаляются, затем приближаются, поэтому наблюдатель в системе K’ будет утверждать:

Когда наблюдатели встретятся, то каждый из них будет утверждать, что он моложе другого. В этом и состоит парадокс часов (персонифицированный вариант – парадокс близнецов).

РИС. 6-10

- момент прибытия часов в точку ;

- показания часов в этот же момент времени;

Разрешение парадокса состоит в том, что ускорение, торможение и поворот – это движение в неинерциальных системах отсчета. Силы инерции эквивалентны силам тяжести. Согласно ОТО появление гравитационного поля изменяет геометрию пространства-времени: там, где существует сила тяжести, ход часов замедляется (потенциал гравитационного поля влияет на ход часов). Значит, в системе, которая претерпевает ускорение, часы идут медленнее; по движущимся часам кажется, что прошел час, а на самом деле (с точки зрения неподвижного наблюдателя) – сутки или год.

Релятивистская динамика

Мы начинаем построение релятивистской динамики.

Как уже говорилось, процесс этот состоит в том, чтобы создавать 4-мерные векторы, у которых 3-мерная (пространственная) часть – это обычный вектор, а временная (ударение на а) часть исчезает при (принцип соответствия).

Почему мы должны поступать таким образом?

- Неинвариантность уравнений Ньютона относительно преобразований Лоренца.

- Неопределенность понятия силы из-за неинвариантности пространственного расстояния относительно преобразований Лоренца и т.д.

Нужно обеспечить инвариантность уравнений механики относительно релятивистских преобразований координат и времени.

4-мерный вектор скорости

4-мерный вектор скорости будем искать как производную 4-мерного радиус - вектора по временному интервалу. В качестве временного интервала возьмем собственное время частицы (материальной точки) в мгновенно-сопутствующей системе отсчета.

По аналогии с построением соответствующих величин в обычном (3-мерном) пространстве, где скорость определялась как производная радиус-вектора по времени, , имеем: (здесь - собственное время частицы; - инвариант, в то время как ни , ни инвариантами не являются).

Собственное время мы отсчитываем в мгновенно-сопутствующей системе отсчета K'.

Мгновенно-сопутствующей системой отсчета будем называть систему отсчета, постоянная скорость которой равна мгновенной скорости частицы (скорость 3-мерная).

В мгновенно-сопутствующей системе отсчета K’ за бесконечно малый промежуток времени (в течение которого как раз ) координаты частицы не изменяются: , т. е. частица покоится в мгновенно-сопутствующей системе K’.

Пользуясь высказанными соображениями, введем еще раз понятие собственного времени частицы, связав его с интервалом между событиями.

Интервал инвариантен:

; отсюда с учетом , имеем

- квадрат модуля вектора мгновенной скорости частицы, поэтому

Собственное время частицы: .

Примечание

Поскольку ускорение влияет на ход часов, мы не можем связывать часы с движущейся частицей. Время нужно отсчитывать по часам в неподвижной системе отсчета, переходя к измерению полного собственного времени частицы путем суммирования (интегрирования): .

Вводим 4-мерный вектор скорости: .

К омпоненты скорости (индекс не путать со степенью!):

, .

Убедимся в инвариантности квадрата 4-мерного вектора скорости относительно преобразований Лоренца.

(Дополнительный материал.)

Для этого подставим выражение для интервала вместо dR - и собственное время частицы в выражение для скорости:

invariant.

Заметим, что при множитель , компоненты переходят в , т.е. совпадают с обычной скоростью. Компонента отлична от нуля даже при (частица покоится). При этом . Смысл в том, что время остановить нельзя, оно всегда течет (точнее - летит).

В 4-мерном мире Минковского покоя (в смысле ) – быть не может.

4-мерная сила и 4-мерное уравнение движения

Напоминание 1

Основное уравнение динамики в модели Галилея-Ньютона:

, или , или

( - 3-мерный импульс, - 3-мерная сила).

Напоминание 2

Возьмем уравнение . Умножим правую и левую части на :

( левая часть – изменение энергии системы, правая – работа силы на пути ).

Под знак дифференциала в левой части уравнения можно ввести произвольное постоянное слагаемое (энергия, которой обладает тело в состоянии покоя). Тогда полная энергия тела . Обычно в классической механике выбирают , и полная энергия свободного тела (при ) совпадает с его кинетической энергией.

Напоминание 3

Если частица находится в потенциальном поле , то .

Так как , а , то

; отсюда закон сохранения энергии  .

4-мерный импульс

По аналогии с трехмерным импульсом вводим 4-мерный импульс как произведение инвариантной скалярной массы на 4-мерную скорость, т.е.

, .

Здесь записаны компоненты импульса в виде матрицы.

Отличие от 3-мерного импульса - в множителе, возникающем в результате преобразования скоростей:

Из этой записи возникает распространенное впечатление о зависимости массы частицы от скорости: .

Т огда: .

РИС. 6-11

На самом деле масса инвариантна и не изменяется при переходе от одной ИСО к другой.

Математическое отступление

Матрица – система элементов (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы (таблицы).

Если матрица имеет строк и столбцов, говорят о матрице .

Если , то матрица называется квадратной , а число - ее порядком. Матрица может состоять из одной строки или из одного столбца. Запись матрицы:

Действия над матрицами

Произведением прямоугольной - матрицы на число называется матрица, элементы которой получены из элементов умножением на :

Сумма определяется только для матриц одинакового строения – элементы суммы равны суммам соответствующих элементов:

Умножение матриц определяется только для таких прямоугольных матриц, что число столбцов первого множителя равно числу строк второго множителя.

Произведением матрицы на матрицу будет матрица - такая, что , где , .

Элементы строки умножаются на соответствующие элементы столбца и складываются.

При умножении:

1) нет коммутативности, ; если , то матрицы называются перестановочными;

2) произведение двух ненулевых матриц может быть равно нулевой матрице.

4-мерное уравнение движения (пространственная часть)

(Вывод можно пропустить.)

По аналогии с основным уравнением классической динамики запишем:

( - собственное время частицы).

Компоненты вектора 4-мерной силы еще предстоит определить.

То же уравнение в компонентах:

Определяем компоненты :

;

Используем определение 4-мерного импульса, тогда

Приравнивая 4-мерные векторы, мы приравниваем компоненты:

Чтобы выполнялся принцип соответствия, пространственные компоненты 4-мерной силы должны быть пропорциональны компонентам 3-мерной силы. Тогда при релятивистские уравнения движения перейдут в уравнения Галилея-Ньютона:

, ( - компоненты 3-мерной силы).

Так как , то

= ,  = .

Умножая правую и левую части на соответствующие координатные орты и складывая результаты, получаем:

Это - пространственная часть уравнения движения в релятивистском приближении.

Отличается от классического уравнения лишь определением импульса , да и то можно превратить в классическую форму, если ввести зависящую от скорости массу: .

Временная компонента 4-мерной силы

(Вывод можно пропустить.)

Запишем инварианты 4-мерной скорости:

Продифференцируем уравнение по собственному времени частицы:

Здесь записано то, что нам уже известно о величинах, входящих в дифференциал инварианта. Подставляем:

;

- временная компонента 4-мерной силы.

Найдены компоненты 4-мерной силы Минковского:

Временная компонента релятивистского уравнения движения

Приравниваем соответствующие компоненты и :

Умножаем правую и левую части на :

;

слева - изменение во времени полной энергии свободной релятивистской частицы, справа - работа трехмерной силы .

Пространственно-временное уравнение движения:

(1) - векторное,

(2) - скалярное.

При уравнение (1) переходит в уравнение классической динамики, а уравнение (2) превращается в тождество 00:

делим левую и правую части (2) на , тогда

;

в левой части , поэтому производная равна 0;

в правой части при , поэтому векторное произведение равно 0.

Полная энергия свободной ( ) релятивистской частицы

Запишем пространственно-временное уравнение движения (2):

;

слева, по аналогии с классическим уравнением, изменение полной энергии свободной частицы, справа - работа силы на пути .

Определим полную энергию свободной релятивистской частицы, помня о том, что уравнение (2) дает полную энергию с точностью до постоянной величины:

где и - абсолютная величина 3-мерной скорости частицы.

Из выражения видно, что при , и выясняется, что частица обладает энергией покоя:

Какая величина энергии покоя?

=1 г, =910²⁰см²/с²  10²¹эрг/г10¹⁴ Дж/г.

Примечание

Существенно не то, сколько энергии содержит та или иная система, а то, сколько энергии может быть использовано. До начала использования ядерной энергии энергия покоя никак не реализовывалась, соответственно всегда сохранялась масса (взвешивание всегда было одним из самых точных измерений). Действительно, нагревание 1 кг воды на 100⁰ изменяет массу на 510^-9г, т.е. относительное изменение массы =510^-12 – за пределами точности.