1.11 Построение лчх

Если ПФ ИС задана в D-форме, то для построения ЛЧХ нужно выполнить две операции:

1. Перейти от трансцендентной формы к дробно-рациональной, то есть произвести замену e^q = z и W*(q) = W*(z).

Однако, при этом особый отрезок L на q-плоскости переходит в окружность единичного радиуса на плоскости z.

2. Для построения ЛЧХ необходимо эту окружность преобразовать в мнимую ось и при этом частота будет изменяться от -∞ до +∞. Для этих целей используется так называемое билинейное или W-преобразование.

Для практики удобнее использовать модифицированное w-преобразование:

Методика построения ЛЧХ:

1. ПФ непрерывной части представляют в виде суммы простых слагаемых.

2. Для каждого слагаемого по таблицам операционных соответствий находят z-изображение.

3. Путем суммирования всех слагаемых находят z-передаточную функцию импульсной системы.

W*(z) = TZ{W(s)}

4. Путем подстановки (1.11.1) переходят к ПФ в форме W*(w).

5. Заменяя w= , строят ЛЧХ по выражениям 1.11.3 и 1.11.4.

Пример: ПФ приведенной НЧ имеет вид:

Необходимо построить ЛЧХ импульсной системы с периодом квантования Т.

1) Разложим W(S) на простые слагаемые (1.11.1):

(1.11.1)

2) С помощью таблиц Z - преобразований находим операционные соответствия

3) Найдем ПФ

4) Найдем ПФ

5) ЛЧХ ИС описывается следующими выражениями (1.11.2) и (1.11.3)

(1.11.2)

(1.11.3)

где – эквивалентная постоянная времени.

Рисунок 1.11.1

Kак видно из ЛАХ (рисунок 1.11.1) в облаcти частот ω*<<2/Т ЛАХ непрерывной части L(ω) и импульсной системы L*(ω*) практически совпадают.

Аналогичный вывод можно сделать из теоремы Котельникова-Шеннона. Теорема: чтобы регенерировать (восстановить) непрерывный сигнал из входного дискретного частота квантования ω₀ должна быть больше удвоенного значения максимальной частоты ω_m или равна ему. . Для систем автоматического управления с единичной ОС величину ω_m ограничивают полосой пропускания, при этом .

Таким образом

(1.11.4)

При выполнении последнего условия, то есть когда частота среза меньше 2/Т импульсную систему можно считать непрерывной. Поскольку в рассмотренном примере частоты сопряжения множителей лежат далеко за частотой среза, то они практически на свойства системы влияние не оказывают. В сложных случаях для построения ЛЧХ используют приближенный метод.

1.12 Приближенный метод

Приближенный метод построения ЛЧХ основан на следующих допущениях:

1. Частота среза системы принадлежит НЧ области, т.е. ω_с<2/Т, где Т – период следования импульса.

2.) ПФ приведенной непрерывной части описывается только звеньями первого порядка

(1.12.1)

Кν – добротность, ν – порядок астатизма.

3.) Звенья знаменателя с постоянными времени Т₁…Т_n можно разделить на две группы:

T_i > Т/2, i=1,q

Т_i < Т/2, i= q+1, n

Звенья передаточной функции непрерывной части разделяются на низкочастотные и высокочастотные, в зависимости от того где находятся частоты сопряжения . При ω_i<2/T – низкочастотная (НЧ) область, при ω_i >2/Т – высокочастотная (ВЧ) область.

4. Звенья числителя формируют НЧ область

5. Пересечение асимптот ЛАХ с вертикальной прямой возможно при наклонах «-20дБ/дек» и «-40дб/дек».

Рассмотрим эти случаи отдельно.

Случай 1. Пересечение вертикальной прямой с первой асимптотой ВЧ области ЛАХ при наклоне «-20дБ/дек» .

ПФ ВЧ области запишем в виде:

, (1.12.2)

где ω_ов – базовая частота. Определяется как частота пересечения первой асимптоты ВЧ области с осью частот (рисунок 1.12.1).

Рисунок 1.12.1

Рассмотрим вначале простой случай: (1.12.3)

ЛАХ ВЧ области имеет вид (рисунок 1.12.2)

Рисунок 1.12.2

Построим ЛАХ импульсной системы, соответствующей выражению (1.12.3). Разложим выражение (1.12.3) на простые слагаемые:

(1.12.4)

Затем используя таблицу Z-преобразований, запишем

(1.12.5)

Используя W-преобразование , получим:

(1.12.6)

- эквивалентная постоянная времени, гиперболический котангенс определяется выражением: , при , , .

ПФ импульсной системы в ВЧ области принимает вид:

. (1.12.7)

Тогда импульсной системе соответствует ЛАХ , а непрерывной - (рисунок 1.12.3).

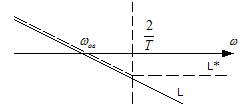
Рисунок 1.12.3

Для ПФ (1.12.6) выражения ЛЧХ имеют вид:

(1.12.8)

(1.12.9)

Рисунок 1.12.4

В более сложном случае (1.12.2), ПФ ВЧ области представляют в приближенном виде:

, (1.12.10)

наибольшая постоянная времени,

(1.12.11)

Если , то можно ограничиться первым членом разложения ПФ звена запаздывания в ряд Тейлора:

.

ПФ дополнительного множителя имеет вид

(1.12.12)

При τ₀=0, , при τ₀=Т,

Применим w-преобразование к выражению (1.12.12).

(1.2.13)

ПФ ВЧ области импульсной системы в этом случае имеет вид:

(1.12.14)

Для ПФ (1.12.14) выражения ЛЧХ имеют вид:

(1.12.15)

(1.12.16)

Стыковку ЛАХ НЧ и ВЧ областей проводят на вертикальной прямой (рис.1.12.5).

Рисунок 1.12.5

Случай 2. Пересечение с вертикальной прямой первой асимптоты ВЧ области ЛАХ при наклоне «-40дБ/дек».

ПФ ВЧ области запишем в виде:

, (1.12.17)

Рассмотрим вначале простой случай: (1.12.18)

(1.12.19)

(1.12.20)

ЛАХ ВЧ области импульсной системы:

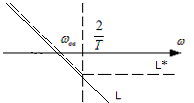
Рисунок 1.12.6

Для ПФ (1.12.20) выражения ЛЧХ имеют вид:

(1.12.21)

(1.12.22)

В более сложном случае, ПФ ВЧ области представляют в виде:

(1.12.23)

(1.12.24)

Для ПФ (1.12.24) выражения ЛЧХ имеют вид:

(1.12.25)

(1.12.26)

ЛАХ ВЧ области импульсной системы:

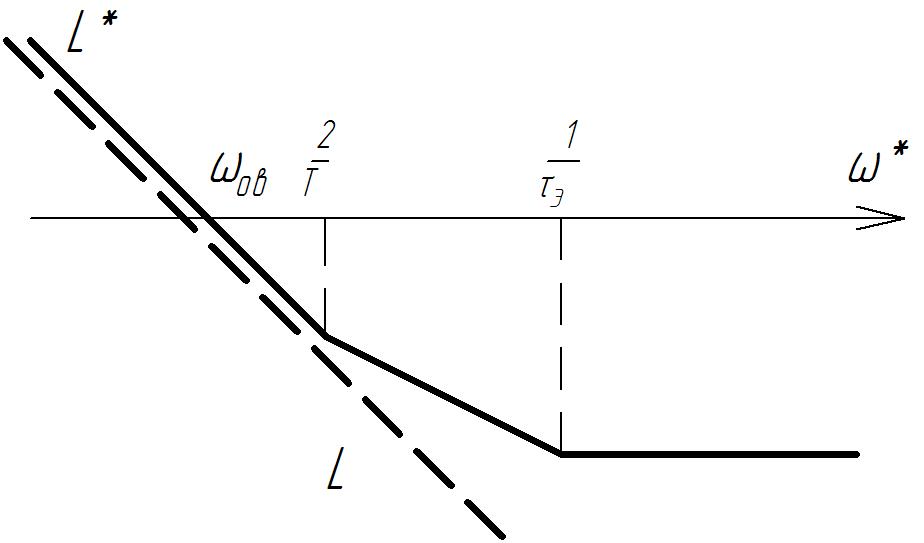
Рисунок 1.12.7