1.2 Примеры импульсных систем

1. Множительное устройство с амплитудно-широтно-импульсной модуляцией

Данное устройство предназначено для перемножения двух напряжений U₁ и U₂

Одно из напряжений соответствует амплитуде импульса, другое - ширине импульса.

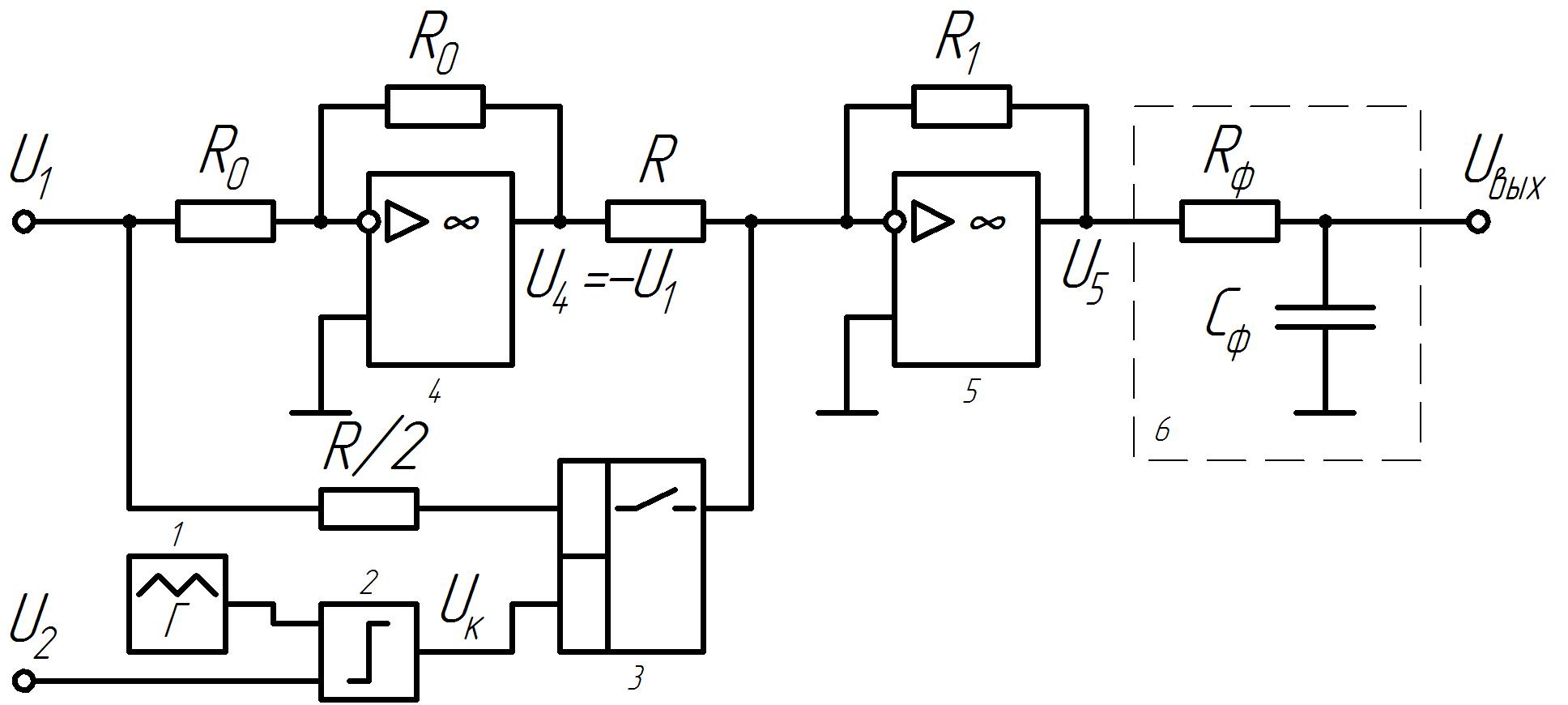
1 – генератор треугольных импульсов,

2 – компаратор,

3 – ключ,

4 – инвертор,

5 - усилитель – сумматор,

6 – фильтр.

Рисунок 1.2.1 – Множительное устройство с амплитудно-широтно-импульсной модуляцией

В компараторе 2 сравниваются напряжения генератора Г и напряжение U₂.

Выходное напряжение инвертора 4:

Если U₂ = 0, то импульсы с генератора 1 поступают на вход компаратора 2 несмещённые. В этом случае ключ 3 будет закрыт и открыт одинаковые промежутки времени. На выходе получаются импульсы с одинаковой амплитудой и длительностью (t1 = t2) , но разных знаков (рисунок 1.2.2).

Рисунок 1.2.2

При разомкнутом ключе (3):

При замкнутом ключе: , среднее за период Т напряжение на выходе сумматора 5 . Рассмотрим случай U₂>0.

Рисунок 1.2.3

Из подобия треугольников можно записать , тогда

2. Импульсный фильтр

Импульсный фильтр - устройство, реагирующее на значения входного сигнала в дискретные равноотстоящие моменты времени.

Ключ представляет собой амплитудный импульсный модулятор. Входной сигнал рассмотрим в виде гармонического сигнала .

Если частота ключа совпадает с частотой входного сигнала , то напряжение нагрузки представляет собой последовательность импульсов постоянной величины (рисунок 1.2.4).

Рисунок 1.2.4

Если не совпадает с частотой входного сигнала , то на выходе появляется в виде последовательности импульсов, огибающая которых будет изменяется с разностной частотой

(1.2.1)

r – ближайшее к целому отношение

Рисунок 1.2.5

Пример применения: устранение периодических помех.

Входной сигнал содержит периодическую помеху: .

- полезный сигнал

- помеха с частотой ω₂

Фильтр устраняет помеху (рисунок 1.2.6)

Рисунок 1.2.6

Если выбрать частоту ключа и обеспечить синфазность в дискретные моменты времени , то

1.3 Решетчатые функции

Решетчатыми называются функции, значение которых определяется только в дискретные равностоящие значения независимой переменной (моменты времени). Между этими дискретными значениями решетчатая функция равна нулю (рисунок 1.3.1).

Рисунок 1.3.1

Решетчатая функция (РФ) обозначается f[nT], где T- положительная величина. Определяющая расстояние между дискретами, n- целое число. Для переход от непрерывной функции к РФ нужно заменить t = nT

f(t)=e^kt , f[nT]= e^knT

Так как между дискретными значениями решетчатая функция равна нулю, то для определения значения функции между дискретами вводится понятие смещённой решетчатой функции: f[nT+∆t]=f[nT,∆t], -T< <+T .Рассматривая ∆t как параметр можно определить выходной сигнал в любой момент времени, то есть импульсный сигнал представить как непрерывную функцию.

Одной и той же решетчатой функции могут соответствовать различные непрерывные и разрывные функции, если их ординаты в дискретные моменты времени соответствуют дискретам решетчатых функций. Такие функции называют огибающими решетчатых функций

Рисунок 1.3.2

Простейшей огибающей решетчатой функцией является ступенчатая функция, проведенная через вершину дискрет (рисунок 1.3.2).

Если ввести переменную и расстояние между дискретами будет равно единице. РФ, соответствующая непрерывной будет иметь вид .