2. Последовательное программирование

Правую часть выражения (2.13.3.2) произвольным образом запишем в виде произведения двух функций.

Рисунок 2.13.3.4

3. Параллельное программирование.

Правую часть выражения (2.13.3.2) разложим на сумму элементарных дробей.

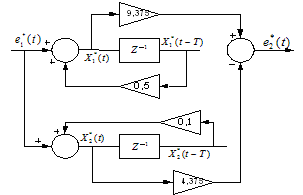
Рисунок 2.13.3.5

2.13.4 Сравнительный анализ методов программирования

С точки зрения эффективности вычислений метод последовательного программирования является наиболее удобным, так как требует меньшего объема памяти и числа арифметических устройств. К тому же МПП позволяет обеспечить экспериментальный выбор и коррекцию программы ЦВМ, поскольку нули и полюса звеньев являются нулями и полюсами ЦКУ. Однако, если необходимо уменьшить запаздывание, вносимое ЦВМ в контур системы управления, то есть снизить время на вычисления, целесообразно применять метод непосредственного программирования. Этот метод вносит наименьшее запаздывание в систему, так как все члены разностного уравнения, за исключением можно вычислить до подачи входного сигнала е₁(t). Кроме того, иногда МНП рационален и с точки зрения используемого оборудования. Это имеет место, например, для ЦКУ, Wk(Z) которых имеет несколько коэффициентов равных нулю.

Метод параллельного программирования обеспечивает высокое быстродействие, но требует большого объема оборудования, что ограничивает применение.

2.14 О точности задания коэффициентов цифрового корректирующего устройства

Рассмотрим случай, когда в результате синтеза получено цифровое КУ в виде апериодического звена

(2.14.1)

Произведем подстановку .

Выражение (2.14.3) устанавливает взаимосвязь между коэффициентом а и постоянной Т1 с периодом дискретности Т. При реализации цифрового КУ с ПФ (2.14.2) неизбежно округление коэффициента а вследствие ограниченности разрядной сетки цифровой части. Обозначим эту погрешность через а и найдем абсолютную погрешность задания постоянной Т1.

(2.14.4)

Относительная погрешность реализации заданного значения Т1:

Выражение (2.14.6) может служить для формирования требований к точности реализации коэффициента а в цифровой части и, в частности, к допустимому округлению а за счет ограниченности разрядной сетки. Эти требования ужесточаются с уменьшением периода дискретности Т.

Второй случай: апериодическое звено второго порядка, Т1 ≠ Т2

Выражение (2.14.8) удобно для последовательного программирования. Для непосредственного программирования выражение (2.14.8) представим в виде:

При реализации цифрового КУ с ПФ (2.14.9) необходимо установить (задать) коэффициенты а₁, а₂ и с. Найдем взаимосвязь между отклонениями коэффициентов а₁ и а.

(2.14.13)

При близких значениях a и b числитель в выражении (2.14.13) а намного больше a-b. Это приведет к тому, что а >>а₁. В результате требования по реализации коэффициента а₁ оказываются значительно более жесткими, чем для а и b. При росте порядка знаменателя Wk(z) требования могут стать настолько жесткими, что реализация их не может быть осуществлена из-за ограничения по числу разрядов ЦВМ.

Для устранения этого недостатка переходят от непосредственного программирования к параллельному. В обоих случаях передаточные функции W_ki(z) имеют вид (2.14.2) или близкий к нему. Требования к точности реализации коэффициентов а и b при этом определяются выражением (2.14.6) и оказываются не такими жесткими по сравнению с непосредственным программированием.