2.5 Аналого-цифровое преобразование (ацп)
Процесс преобразования непрерывного сигнала в машинный код. Процесс более сложный, чем цифро-аналоговое преобразование и занимает больше времени. АЦП имеет большую стоимость, чем ЦАП и меньшую точность.
Структурно аналого-цифровой преобразователь можно представить состоящим из УВХ, квантователя по уровню, шифратора (рисунок 2.5.1).
Рисунок 2.5.1 – Схема АЦП
Рассмотрим АЦП с поразрядным уравновешиванием (рисунок 2.5.2).
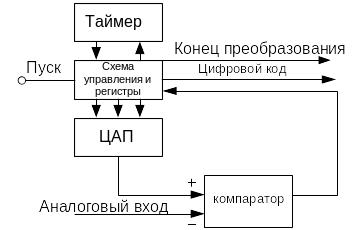
Рисунок 2.5.2 – Схема АЦП с поразрядным уравновешиванием
Вначале преобразование все разряды ЦАП устанавливаются в ноль (операция очистки). Затем в старший разряд ЦАП записывается 1, что соответствует примерно половине максимального числа.
В компараторе происходит сравнение сигнала ЦАП и аналогового сигнала.
Если уровень аналогового сигнала превышает уровень напряжения ЦАП, то «1» сохраняется, если нет – то в этом старшем разряде записывается «0». Аналогичным образом сравнение ведется до самого младшего бита, после чего вырабатывается сигнал «конец прерывания» и цифровой код готов к передаче.
От числа двоичных разрядов АЦП зависит его точность, а от методов преобразования – время преобразования.
2.6 Цифровые сау с экстраполятором нулевого порядка
Рассмотрим случай когда на ЦВМ возлагается задача вычисления ошибки рассогласования, в этом случае D(z)=1. Пренебрежем квантованием по уровню, т.е. будем рассматривать ЦВМ как импульсную систему. Рассмотрим определение ПФ экстраполятора нулевого порядка.
Рис. 2.6.1.
Из рисунка 2.6.1 следует, что импульсный элемент совместно с Э0 генерирует импульсы прямоугольной формы с длительностью, равной периоду дискретности Т.
ПФ Э0 можно найти двумя способами:
а) путем интегрирования импульса единичной амплитуды
(2.6.1)
б)
путем нахождения изображения разности
двух сдвинутых на величину Т единичных
сигналов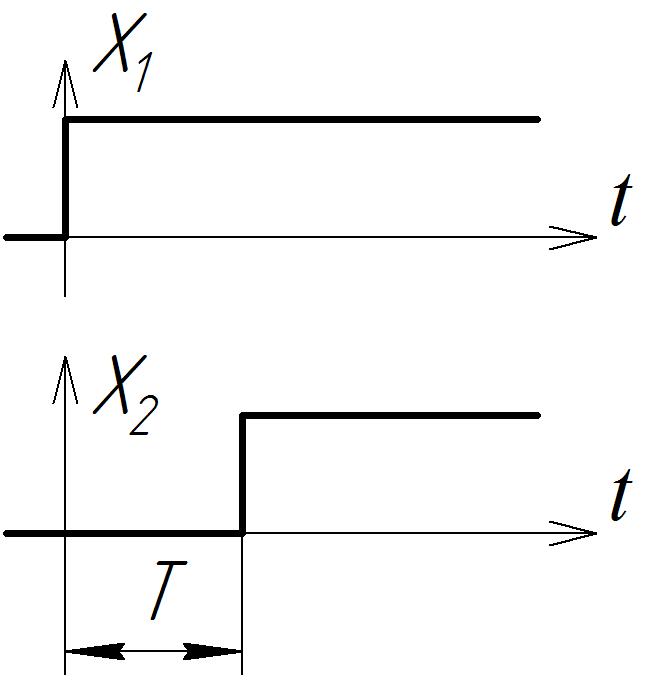
Объединяя ПФ экстраполятора с ПФ непрерывной части W0(s) получим ПФ приведенной непрерывной части:
(2.6.2)
ПФ дискретной системы:
(2.6.3)
В соответствии со свойствами z – преобразования Z -множители можно вынести. В итоге передаточная функция разомкнутой цифровой системы с экстраполятором нулевого порядка имеет вид:
(2.6.4)
Для нахождения W*(z), выражение в фигурных скобках раскладывается на простые слагаемые. Затем для каждого слагаемого по таблице соответствия находится соответственное z – преобразование.
Если
имеется чистое запаздывание
то
Рассмотрим частотные характеристики экстраполятора Э0 . Передаточную функцию (2.6.1) экстраполятора Э0 путем замены S=jω представим в виде
(2.6.5)
Поскольку Т – период квантования и Т = 2π/ω0, то можно записать:
(2.6.6)
АЧХ и ФЧХ Э0 имеют следующий вид
Поскольку
при
меняет знак, то на частотах кратных ω0
ФЧХ φэ(ω)
ступенчато прирастает на величину –π.
В общем случае функциональная схема САУ с экстраполятором нулевого порядка:
Для
нахождения
выражение
раскладывают на простые слагаемые, а
затем пользуются таблицами z-преобразования.
Если
в канале управления имеется временное
запаздывание
,
то
Пример. Определим ПФ разомкнутой системы для случая, когда непрерывной часть имеет ПФ:
,
,
,
.
разложим
на простые слагаемые:
,
,
,
,
