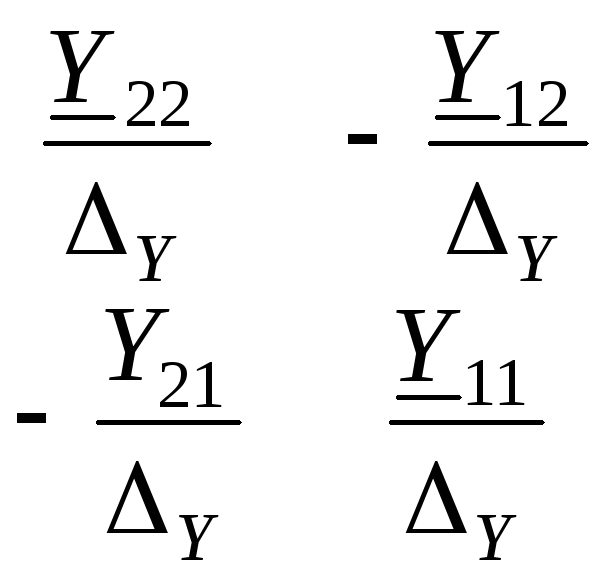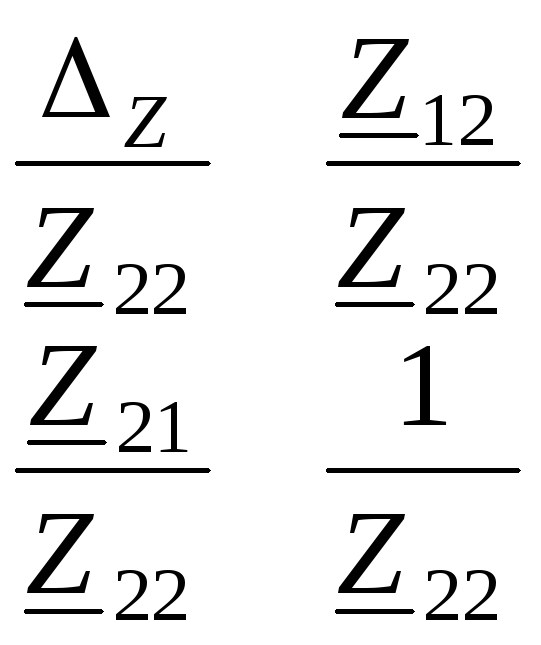- •Билет№1
- •2. Четырехполюсники. Понятие, классификация. Обратимость четырехполюсников.
- •Классификация четырехполюсников
- •Режим обратного питания четырехполюсников
- •Билет№2
- •1.Причины возникновения переходного процесса.
- •2.Система уравнений четырехполюсника. Понятие симметрии четырехполюсника. Основные уравнения четырехполюсников
- •3.3. Режим обратного питания четырехполюсников
- •Симметричный четырехполюсник
- •Билет№3
- •1.Составление дифференциальных уравнений цепи. Принципы решения дифференциальных уравнений. Классический метод. Классический метод расчета
- •Классический метод расчёта переходных процессов
- •2.Виды соединений нескольких четырехполюсников. Соединения четырехполюсников
- •3.13.1. Каскадное соединение
- •3.13.2. Параллельное соединение
- •3.11.3. Последовательное соединение
- •Билет№4
- •1.Начальные условия. Законы коммутации.
- •Общая характеристика переходных процессов
- •2.Четырехполюсники в форме ||z|| параметров.
- •Билет№5
- •1.Классический метод расчета переходных процессов.
- •Классический метод расчета
- •2.Четырехполюсники в форме ||а|| параметров. Условие его обратимости.
- •Определение а–параметров с помощью режимов короткого замыкания и холостого хода
- •Билет№6
- •1.Подключение цепи r,l к источнику энергии. Время переходного процесса.
- •2.Характеристические параметры четырехполюсника: согласованные сопротивления, мера передачи. Характеристические параметры четырехполюсника
- •Билет№7
- •1.Замыкание цепи r,l с накопленной энергией на себя. Время переходного процесса.
- •2.Четырехполюсник в форме ||а|| параметров в гиперболических функциях. Уравнения четырехполюсника в гиперболических функциях
- •Билет№8
- •1.Подключения цепи r,c к источнику энергии. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при последовательном, параллельном и каскадном соединении нескольких четырехполюсников.
- •Билет№9
- •1.Замыкание цепи r,c с накопленной энергией на себя. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при смешанном соединении нескольких четырехполюсников. . Эквивалентные схемы замещения четырехполюсника
- •Билет№10
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при действительных корнях характеристического уравнения.
- •4.2.6.1. Разряд емкости на цепь rl
- •Билет№11
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при комплексно-сопряженных корнях характеристического уравнения.
- •2.Вторичные параметры четырехполюсника. Примеры их нахождения. Билет№12
- •1.Подключения цепи r,l,c к источнику энергии. Время переходного процесса.
- •Переходные процессы при подключении последовательной r-l-c-цепи к источнику напряжения
- •2.Электрические фильтры понятие и классификация.
- •Билет№13
- •1.Замыкание цепи r,l,c с накопленной энергией на себя. Время переходного процесса.
- •2.Полоса пропускания и полоса задержки электрических фильтров. Граничные частоты пропускания реактивных фильтров.
2.Система уравнений четырехполюсника. Понятие симметрии четырехполюсника. Основные уравнения четырехполюсников
П ринято
условно изображать четырехполюсники
так, как это показано на рис. 3.1. Это
«проходной» четырехполюсник. В нем
электрическая энергия передается слева
направо. Одну пару выводов называютпервичной
(входной), а
другую – вторичной
(выходной)
и обозначают соответственно 1–1
и 2–2.
Входной ток обозначают
ринято
условно изображать четырехполюсники
так, как это показано на рис. 3.1. Это
«проходной» четырехполюсник. В нем
электрическая энергия передается слева
направо. Одну пару выводов называютпервичной
(входной), а
другую – вторичной
(выходной)
и обозначают соответственно 1–1
и 2–2.
Входной ток обозначают
![]() ,
входное напряжение –
,
входное напряжение –![]() ,
ток и напряжение на выходе –
,
ток и напряжение на выходе –![]() и
и![]() .
Четырехполюсник является передаточным
звеном между источником питания и
нагрузкой. К выводам 1–1,
как правило, присоединяется источник
питания; к выводам 2–2
– нагрузка.
.
Четырехполюсник является передаточным
звеном между источником питания и
нагрузкой. К выводам 1–1,
как правило, присоединяется источник
питания; к выводам 2–2
– нагрузка.
З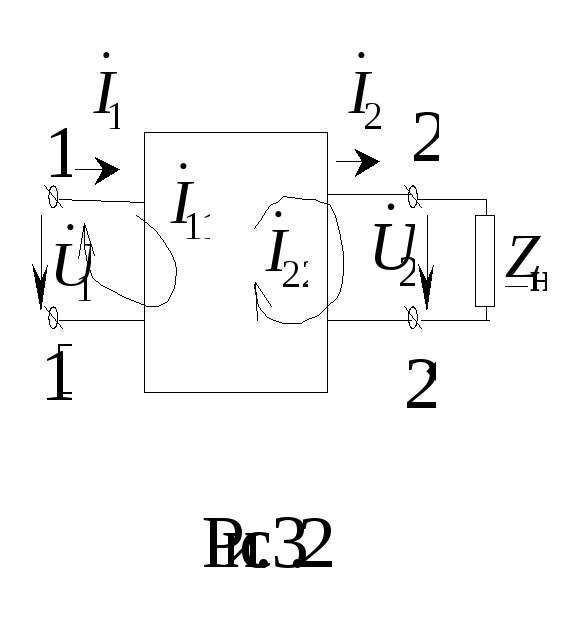 ависимости
между двумя напряжениями и двумя токами,
определяющими режим на первичных и
вторичных выводах, могут быть записаны
в различной форме. Если считать две из
указанных величин заданными, то две
другие величины будут связаны с ними
системой двух уравнений, которые
называютсяуравнениями
четырехполюсника.
ависимости
между двумя напряжениями и двумя токами,
определяющими режим на первичных и
вторичных выводах, могут быть записаны
в различной форме. Если считать две из
указанных величин заданными, то две
другие величины будут связаны с ними
системой двух уравнений, которые
называютсяуравнениями
четырехполюсника.
Пусть схема
четырехполюсника содержит n
независимых контуров. В качестве первого
(рис. 3.2) выберем контур, включающий в
себя источник энергии на зажимах 1–1,
в качестве второго – контур, включающий
в себя приемник, присоединенный к зажимам
2–2.
Будем рассматривать напряжение на
входных зажимах четырехполюсника
![]() как входное напряжение. Такое включение
принято называтьпрямым.
как входное напряжение. Такое включение
принято называтьпрямым.
Составим уравнения по методу контурных токов.
 (3.1)
(3.1)
Поскольку
![]() ,
то, перенеся величину
,
то, перенеся величину![]() в правую часть второго уравнения,
приведем систему уравнений к виду
в правую часть второго уравнения,
приведем систему уравнений к виду
 (3.2)
(3.2)
Учитывая, что правые части всех уравнений, кроме первых двух, равны нулю, получим на основании принципа наложения следующее решение
 (3.3)
(3.3)
Коэффициенты в (3.3) имеют размерность проводимости, введем соответствующие обозначения
![]() .
.
Тогда уравнения четырехполюсника, записанные в Y-форме, связывающие токи с напряжениями, имеют вид
 (3.4)
(3.4)
Полученные соотношения в матричной форме имеют вид:
![]() .
.
Для
линейной пассивной цепи
![]() ,
а следовательно,
,
а следовательно,![]() .
Из четырехY-параметров
независимых три, т.к.
.
Из четырехY-параметров
независимых три, т.к.
![]()
Решив
(3.4) относительно напряжений
![]() и
и![]() ,
получим уравнения четырехполюсника,
записанные вZ-форме,
связывающие напряжения и токи
,
получим уравнения четырехполюсника,
записанные вZ-форме,
связывающие напряжения и токи
 (3.5)
(3.5)
где
 (3.6)
(3.6)
при
этом
![]() .
.
Из четырех Z–параметров независимых три.
Уравнение (3.5) в матричной форме:
![]() .
.
Наиболее распространенной формой записи уравнений четырехполюсника является такая, при которой входные ток и напряжение выражаются через выходные напряжение и ток. Из уравнений (3.3) можно записать
 . (3.7)
. (3.7)
Подставим (3.7) в первое уравнение (3.3)
 (3.8)
(3.8)
Введем обозначения
![]() –величина
безразмерная;
–величина
безразмерная;
![]() –величина,
измеряемая в омах;
–величина,
измеряемая в омах;
![]() –величина,
измеряемая в сименсах;
–величина,
измеряемая в сименсах;
![]() –величина
безразмерная.
–величина
безразмерная.
При этом будут справедливы соотношения
![]() (3.9)
(3.9)
В матричной форме эти уравнения имеют вид

Уравнения
(3.9) называют уравнения
четырехполюсника в А-параметрах.
Учитывая,
что
![]() ,
можно показать, что определитель матрицыА равен
единице:
,
можно показать, что определитель матрицыА равен
единице:
 (3.10)
(3.10)
Итак:
![]()
Из
этого соотношения следует, что для
определения
![]() и
и![]() достаточно знать только три коэффициента
из четырех, т.е. средиА–параметров
только три независимые, аналогично для
Z–,
Y–
форм.
достаточно знать только три коэффициента
из четырех, т.е. средиА–параметров
только три независимые, аналогично для
Z–,
Y–
форм.
Таким образом, зная, что Y, Z, A – параметры зависят от параметров элементов и конфигурации схемы четырехполюсника, можно сформулировать связь вход–выход, не прибегая к расчету токов и напряжений во внутренней части четырехполюсника, которая может представлять собой весьма сложную электрическую цепь.
Имеются и другие соотношения, связывающие в смешанной форме токи и напряжения на входе и выходе четырехполюсника. Приведем без вывода уравнения четырехполюсника в H – и G – параметрах:
 .
.
Все параметры в общем случае – комплексные числа. Соотношения, связывающие между собой параметры в различных формах записи, приведены в табл. 3.1.
Таблица 3.1
|
Определ параметр |
Z |
Y |
H |
A |
|
Z |
|
|
|
|
|
Y |
|
|
|
|
|
H |
|
|
|
|
|
A |
|
|
|
|
|
Примечание.
В таблице обозначены:
| ||||
Рассмотрим наиболее подробно уравнения четырехполюсника в А – параметрах.