12

СПЕКТРЫ ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ

Определим вещественный спектр

Рис. 7.7

т.к. функция симметрична относительно оси ординат: А^’_k = 0

т.о.

Спектрограмма АЧХ вещественного спектра выглядит следующим образом:

Рис. 7.8

Для данной последовательности импульсов можно сделать следующие выводы:

1. положение нулей определяется длительностью импульса

2 p/ t_и ; 4 p/ t_и и т.д.

2. Амплитуда гармонических составляющих зависит от всех 3-х значений параметров сигнала E, T, t :

3. Расстояние между спектральными линиями определяется периодом Т .

4. Количество спектральных линий в лепестке диаграммы определяется скважностью последовательности.

от 0 до p .

Рассмотрим несколько сигналов.

Рис. 7.9 (а)

Рис. 7.9 (б)

Функции симметричны относительно оси ординат

А^’_k = 0

Вычислим вещественный спектр для случая а):

(Пределы от t /2 до 0, поэтому умножается на 2).

0 1 2 3 4 5

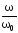
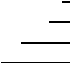
(Пропорционально ).

Рис. 7.10

Рассмотрим сигнал U₂ (t)

Рис. 7.11

СПЕКТР ФУНКЦИИ И ИНТЕГРАЛ ФУРЬЕ

Ряд Фурье – это тригонометрический ряд, представляющий собой изображение периодической функции суммой синусоид, амплитуды которых конечны, а аргументы кратны основной частоте w₀ .

Под интегралом Фурье понимают тригонометрический ряд, представляющий непериодическую функцию суммой бесконечно большого числа синусоид, амплитуды которых бесконечно малы, а аргументы соседних синусоид отличаются на бесконечно малую величину.

Формулу для интеграла Фурье получают из формулы для ряда Фурье при Т ¥ .

Опустив ряд преобразований:

- спектральная плотность или спектр функции f(t) .

Вышенаписанные формулы называют парой преобразований Фурье.

Рисунок 7.12 иллюстрирует возможный переход от периодической последовательности прямоугольных импульсов к непериодическому сигналу в виде одиночного импульса путем увеличения периода до бесконечности.

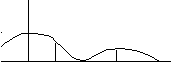
(а)

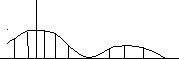
(б)

(в)

(г)

Рис. 7.12

При увеличении Т отдельные спектральные составляющие располагаются ближе друг к другу, а амплитуда становится все меньше. При Т ¥ промежутки между соседними спектральными составляющими должны исчезнуть, т.к. . С этим связана 1-я трудность представления периодического сигнала рядом Фурье – отдельные составляющие спектра невозможно пронумеровать, чтобы использовать запись сигнала в виде ряда соответствующих слагаемых.2-я трудность связана с тем, что амплитудная спектральная составляющая при увеличении

Т 0 . Следовательно, определение спектра теряет смысл.

Говоря о спектрах можно отметить следующее: периодическая функция характеризуется дискретным спектром частот, в то время как непериодическая – непрерывным.

Применение прямого преобразования Фурье дает возможность определить, в частности спектры входных воздействий.

Комплексная функция частоты S(jw) дает закон изменения комплексных амплитудных гармоник в зависимости от частоты w и называется спектральной плотностью или спектральной функцией f(t), S(w) называется амплитудно-частотной характеристикой спектральной плотности, j(w) – фазо-частотной характеристикой спектральной плотности.

В качестве примера определим спектральные плотности некоторых сигналов – функций f(t). На рисунке 7.13 построен прямоугольный импульс длительностью t , высотой а_max .

Его АЧХ представлена

на рис. 7.14.

.

Рис. 7.14

При другой форме импульса получится и иной спектр. Так для несинусоидального импульса f(t) = a_m cos w₀ t длительностью t спектральная плотность

Рис. 7.15

;

.

.

АЧХ S(w) изображена на рис. 7.16.