12

^{УРАВНЕНИЯ} СЛОЖНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ В МАТРИЧНОЙ ФОРМЕ.

Два двухполюсника можно соединить или параллельно, или последовательно. Число способов, которыми можно соединить два четырехполюсника значительно больше.

Рассмотрим некоторые способы соединения четырехполюсников:

1. Последовательное соединение (см. рис. 3.6)

Рис. 3.6

Одноименные порты соединены последовательно.

Так как , а в каждом порте один и тот же ток протекает по обоим четырехполюсникам, то уравнения состояния цепи примут вид:

Следовательно, при последовательном соединении четырехполюсников их Z матрицы суммируются.

[ Z ] = [ Z_I ] + [ Z_II ]

2. Параллельное соединение

I

II

Рис. 3.7

Уравнения составных четырехполюсников в матричной форме:

Таким образом, [ Y ] матрица результирующего четырехполюсника равна сумме матриц составных четырехполюсников.

3. Последовательно-параллельное соединение (см. рис. 3.8).

I

II

Рис. 3.8

[ H ] = [ H ]_I + [ H ]_{I I .}

4. Каскадное соединение (см. рис. 3.9).

I

II

Рис. 3.9

[ A ] = [ A ]_I ^. [ A ]_{I I}

(1)

В свою очередь:

(2)

(2) (1) , где

Матричное соединение не коммутативно, то есть

A_IA_II A_IIA_I .

МАТРИЦЫ НЕКОТОРЫХ ЧЕТЫРЕХПОЛЮСНИКОВ.

А) На рис. 3.10 представлена схема Т образного четырехполюсника, который образован тремя двухполюсниками Z₁, Z₂ и Z₃. Чтобы получить Z матрицу этой цепи, запишем уравнения по II закону Кирхгофа, выполняя обход элементов Z₁ и Z₃ со стороны порта 1 и элементов Z₂ и Z₃ со стороны порта 2.

Z₁ Z₂

Z₃

Рис. 3.10

Или

Б) На рис. 3.11 изображена схема П образного четырехполюсника, в состав которого входят линейные двухполюсники с проводимостями Y₁, Y₂, Y₃.

Y₃

Y₁ Y₂

Рис. 3.11

Найдем [ Y ] матрицу данной цепи. Для этого запишем два уравнения по I закону Кирхгофа.

Пример

Найти неопределенную матрицу Y параметров полевого транзистора, схема замещения которого по переменному току в режиме малого сигнала.

С_зс

з с

С_зи С_си I=SU_вх

G_i

и и

Рис. 3.12

Дано: S;

jwC_зи

jwC_зс

jwC_си

Решение:

Основная система уравнений

затвор - 1; сток - 2; исток - 3

Для нахождения Y-параметров рассчитаем токи транзистора в режимах короткого замыкания на различных парах выводов.

Схема опытов короткого замыкания для определения Y-параметров , входящих в 1 столбец неопределенной матрицы проводимости приведен на рисунке:

1 Y₂ I^’₂

I^’₁

E₁ Y₁ Y₃ SU₁₀

I^’₃

U₁₀ Рис. 3.13

2

Находим частичные токи выводов транзистора за счет источника U₁₀ = E₁ соединяющего вывод 1 и остальные выводы (см. рис. 3.13):

Аналогично, используя схемы на рис. 3.14 и 3.15:

1 I₁^’’ Y₂ I₂^’’ 2

Y₁ Y₃

E₂

I₃^’’

U₂₀

Рис. 3.14

Таким образом

I₁^’’’ Y₂ I₂^’’’

Y₁ Y₃

-SU₃₀

I₃^’’’

U₃₀ E₃

Рис. 3.15

РАСЧЕТ ХАРАКТЕРИСТИК ЧЕТЫРЕХПОЛЮСНИКА

В СИСТЕМЕ Z ПАРАМЕТРОВ.

Получим формулы для определения функций цепи в случае, когда математической моделью четырехполюсника (Т типа) служит его Z матрица.

z_н

Рис. 3.16

Дано: U₁, z_н, и система z-параметров для 4-х полюсника, представленного на рис. 3.16.

Определить: K_i , K_u , R_вх.

Решение:

, и

Тогда

Решая систему относительно токов, получим:

Пример: В Т образном четырехполюснике элементы Z₁ и Z₂ представляют собой катушки с одинаковыми индуктивностями L=80 мкГн. Элементом Z₃ служит конденсатор с емкостью C=3 пФ. Чисто резистивная нагрузка цепи имеет сопротивление R_н=600 Ом. Найти численные значения функций цепи K_i, K_u, Z_вх при частоте источника на входе 0.4 МГц.

Решение:

Вычисляем сопротивления элементов, образующих четырехполюсник:

Z₁ = Z₂ = jwL = j201 Ом ;

Z₃ = –j133 Ома.

Таким образом, ток в нагрузке по амплитуде приблезительно в 5 раз меньше, чем на входе, а выходной ток опережает по фазе входной.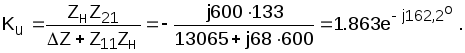

Амплитуда напряжения на выходе почти в 2 раза больше, чем на входе.

Четырехполюсник можно рассматривать как частный случай многополюсника. Обозначение многополюсника с выбранными положительными направлениями токов показано на рис. 3.

.

.

.

Рис. 3.18

Так же как и у четырехполюсника можно записать уравнения связи между напряжениями и токами. Для любого k-ого вывода (k=1,…,n) выполнено:

,

где

– все выводы, кроме i – ого соединены с (n+1)-ым (взаимная проводимость).

I_k⁽ⁱ⁾ – k-ый ток при незакороченном i-ом выводе.

Например: , где

Таких уравнений можно записать n. Следовательно, уравнения связи напряжений и токов можно записать в матричной форме:

Частным случаем многополюсника является, например, операционный усилитель. Его можно считать линейным многополюсником, пока напряжения, подаваемые на него, не превышают допустимых значений. В противном случае, необходимо учитывать нелинейность характеристик.

Обозначение операционного усилителя и эквивалентная схема представлены на рис. 3.19.

–

1

₊ 2

3

4

а)

1 2

R_вх E

3

R_вых

4

б)

Рис. 3.19 а) операционный усилитель

б) эквивалентная схема