Гайдукевич И.В. Эконометрика. Сборник задач

1. Модель парной линейной регрессии

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Модель парной линейной регрессии представляет собой уравнение связи двух переменных x и y вида:

, (1.1)

где x – независимая переменная, y – зависимая переменная (результативный фактор), a, b – параметры регрессии.

Построение уравнения регрессии сводится к оценке его параметров. Для оценки параметров уравнений регрессии используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от его расчетных значений минимальна .

Параметры уравнения (1.1) можно найти по формулам (1.2).

(1.2)

Оценить тесноту линейной связи между факторами x и y можно при помощи коэффициента линейной корреляции, который рассчитывается по формуле (1.3). Коэффициент парной линейной корреляции изменяется в пределах от -1 до 1.

(1.3)

Отрицательное значение коэффициента корреляции говорит об обратной зависимости, а положительное – о прямой зависимости. Если абсолютное значение больше 0,7, то говорят о наличии тесной линейной зависимости между факторами x и y.

Качество уравнения определяют нахождением коэффициента детерминации . Его значение показывает, на сколько процентов разброс значений y от средней объясняется зависимостью от фактора x.

Статистическую значимость коэффициентов регрессии можно проверить нахождением t-статистик Стьюдента по формулам (1.4).

(1.4)

S_a и S_b – стандартные ошибки параметров a и b, которые рассчитываются на основе стандартной ошибки уравнения регрессии S.

, , (1.5)

Коэффициент b считается статистически значимым, если . Критическое значение находят по таблицам Стьюдента при уровне значимости (по умолчанию ) и числе степеней свободы n – 2.

Для коэффициента корреляции также можно найти стандартную ошибку и t-статистику (1.6).

. (1.6)

Статистическую значимость уравнения в целом можно оценить при помощи критерия Фишера. Если расчетное значение F > F_кр, то говорят что уравнение регрессии статистически значимо, в противном случае незначимо или неадекватно. F можно рассчитать по формуле (1.7), а F_кр находят по трем параметрам: уровню значимости , числу степеней свободы n – 2 и количеству независимых переменных 1.

(1.7)

Легко доказать, что для парной линейной регрессии , а . Поэтому для парной линейной регрессии оценка адекватности модели равносильна оценке статистической значимости коэффициентов регрессии и корреляции.

Средняя ошибка аппроксимации рассчитывается по формуле (1.8) и характеризует качество уравнения регрессии. Ошибка аппроксимации в пределах 5 – 7% свидетельствует о хорошем подборе модели к исходным данным.

(1.8)

Важной характеристикой является коэффициент эластичности (см. 1.9). Он показывает, на сколько процентов в среднем изменится результат y от своей средней величины при увеличении фактора x на 1% от его среднего значения.

. (1.9)

Пример 1. По территориям региона приводятся (табл. 1.1) среднедушевой прожиточный минимум в день одного трудоспособного (руб., x) и среднедневная заработная плата (руб., y).

Таблица 1.1

№	X, прожиточный минимум, руб.	Y, з/п, руб.
1	80	135
2	85	150
3	90	138
4	82	156
5	92	167
6	110	200
7	70	140
8	90	162
9	77	155
10	92	165
11	80	162
12	120	175

Требуется:

1. Построить линейное уравнение парной регрессии y от x. Описать экономический смысл параметров уравнения.

2. Оценить степень линейной зависимости факторов и качество уравнения регрессии.

3. Рассчитать среднюю ошибку аппроксимации.

4. Оценить статистическую значимость параметров и уравнения регрессии в целом.

5. Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума, составляющем 107% от среднего уровня.

Решение:

Построим диаграмму рассеяния (рис. 1.1), анализ которой позволяет предположить наличие прямой линейной зависимости между прожиточным минимумом и среднедневной заработной платой.

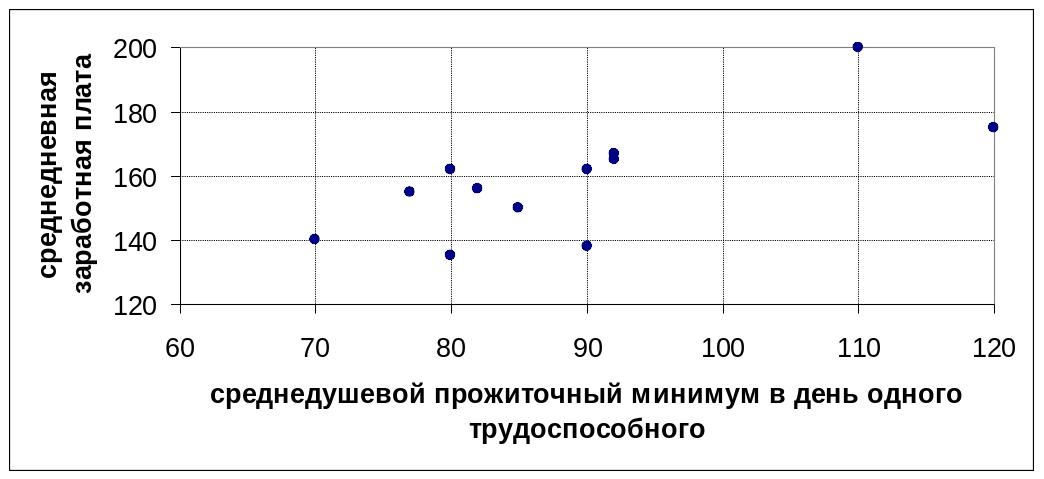
Рис. 1.1. Диаграмма рассеяния

Для расчета параметров уравнения линейной регрессии построим расчетную таблицу (табл. 1.2).

Таблица 1.2

i	x	y	xy	x2	y2			e2	Аi
1	80	135	10800	6400	18225	150,24	-15,24	232,35	11,29%
2	85	150	12750	7225	22500	154,97	-4,97	24,69	3,31%
3	90	138	12420	8100	19044	159,70	-21,70	470,68	15,72%
4	82	156	12792	6724	24336	152,13	3,87	14,95	2,48%
5	92	167	15364	8464	27889	161,59	5,41	29,32	3,24%
6	110	200	22000	12100	40000	178,60	21,40	457,98	10,70%
7	70	140	9800	4900	19600	140,79	-0,79	0,63	0,56%
8	90	162	14580	8100	26244	159,70	2,30	5,31	1,42%
9	77	155	11935	5929	24025	147,41	7,59	57,65	4,90%
10	92	165	15180	8464	27225	161,59	3,41	11,66	2,07%
11	80	162	12960	6400	26244	150,24	11,76	138,23	7,26%
12	120	175	21000	14400	30625	188,05	-13,05	170,35	7,46%
Сумма	1068	1905	171581	97206	305957			1613,79	70,42%
Среднее	89	158,75	14298,42	8100,5	25496,42				5,87%
σ	13,40	17,17
σ2	179,5	294,85

Коэффициенты уравнения регрессии рассчитаем по формулам (1.2).

Итак, получено уравнение регрессии: . С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,95 руб. Свободный коэффициент уравнения экономического смысла не имеет.

Тесноту линейной связи оценит коэффициент корреляции, а качество – коэффициент детерминации.

, .

Т.к. полученный коэффициент корреляции , то можно говорить о наличии достаточно сильной линейной зависимости между факторами x и y. Коэффициент детерминации показывает, что изменение заработной платы на 54% объясняется вариацией фактора x – среднедушевого прожиточного минимума. Качество модели можно считать удовлетворительным.

Определим степень подбора модели к исходным данным при помощи средней ошибки аппроксимации.

.

Качество построенной модели оценивается как хорошее, так как средняя ошибка аппроксимации не превышает 7%.

Определим стандартные ошибки и t-статистики Стьюдента параметров модели.

, ,

.

Тогда

, .

Определим табличное значение t-статистики: для числа степеней свободы df = 10 и уровня значимости α = 0.05: t_табл = 2,23. Т.к. рассчитанные t-статистики больше табличной, то оба параметра являются статистически значимыми, т.е. не случайно отличаются от нуля.

Если прогнозное значение прожиточного минимума составит руб., тогда прогнозное значение среднедневной заработной платы составит: руб.

Проиллюстрируем способ абсолютных приращений для построения точечного прогноза результативного фактора. Для этого необходимо найти абсолютное приращение по переменной x и воспользоваться экономическим смыслом параметра b.

, ,

руб.

Также прогноз результата можно рассчитать, используя коэффициент эластичности.

.

Коэффициент эластичности 0,53 означает, что при увеличении прожиточного минимума на 1% среднедневная зарплата должна увеличиться на 0,53%.

По условию задачи прогноз прожиточного минимума на 7% больше его среднего значения, т.е. , тогда . Т.е. прогнозное значение y на 3,71% больше его среднего уровня.

руб.

Итак, если среднедушевой прожиточный минимум в день одного трудоспособного будет равен 95,23 руб., то среднедневная заработная плата должна составить 164,64 руб.