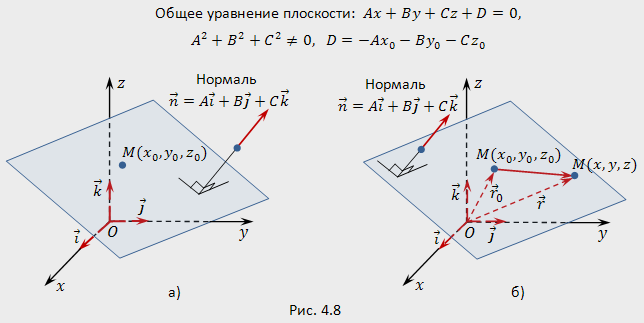
Общее уравнение плоскости
Рассмотрим
произвольную точку 
в
пространстве и некоторый вектор 
Очевидно,
что геометрическим местом точек 
таких,
что вектор 
перпендикулярен
вектору 
будет
плоскость, проходящая через
точку M перпендикулярно
прямой, для которой вектор 
является
направляющим. Нашей задачей будет
установить уравнение плоскости, то есть
найти соотношение, которому удовлетворяют
координаты точки A.
Запишем условие перпендикулярности векторов с использованием скалярного произведения:
|
Запишем последнее равенство в координатах:
|
Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду
|
Обозначая 
получим
|
Это и есть так называемое общее уравнение плоскости.
6.
Вывод уравнения плоскости, проходящей через точку, перпендикулярно вектору, и проходящей через 3 точки.
Требуется
составить уравнение плоскости, проходящей
через точку 
перпендикулярно
вектору 
Выберем
в пространстве произвольную точку 
.
Обозначим 
—
радиус-векторы точек
и
Точка 
принадлежит
заданной плоскости тогда и только тогда,
когда векторы 
и 
перпендикулярны
(рис.4.8,б). Условие ортогональности
запишем при помощи скалярного произведения:
Учитывая,
что 
,
получаем векторное
уравнение плоскости:
Пусть
в координатном пространстве 
заданы
три точки 
не
лежащие на одной прямой (рис.4.17). Требуется
составить уравнение плоскости, проходящей
через заданные точки.
Точка
принадлежит
плоскости, проходящей через точки 
тогда
и только тогда, когда ее
радиус-вектор 
удовлетворяет
условию:
где 
-
некоторые действительные числа
(параметры). Это уравнение, а также его
координатную форму
будем
называть аффинным
уравнением плоскости, проходящей через
точки
Используя векторы
и
в качестве направляющих векторов плоскости, составим уравнение вида (4.18): которое называется уравнением плоскости, проходящей через три заданные точки.
7
Канонические и параметрические уравнения прямой в пространстве
Параметрические и канонические уравнения прямой.
Определение. Любой ненулевой вектор, коллинеарный данной прямой называется ее направляющим вектором.
Пусть
L – произвольная прямая и 
–
ее произвольная, но фиксированная точка,
О – начало координат, 
–
произвольная (текущая) точка прямой
L, 
–
радиус вектор точки 
, 
–
радиус вектор текущей точки М, 
–
произвольный направляющий вектор прямой
L.
рис.5.
Теорема. Следующая система уравнений является параметрическими уравнениями прямой:
, 
,
(7)
где 
– координаты произвольной
фиксированной точки данной прямой, 
–
соответствующие координаты произвольного
направляющего вектора данной
прямой, t – параметр.
Доказательство. В соответствии с определением уравнения любого множества точек координатного пространства, мы должны доказать, что уравнениям (7) удовлетворяют все точки прямой L и, с другой стороны, не удовлетворяют координаты точки не лежащей на прямой.
Пусть
произвольная точка 
.
Тогда векторы 
и 
являются
по определению коллинеарными и по
теореме о коллинеарности двух векторов следует,
что один из них линейно выражается через
другой, т.е. найдется такое число
,
что 
.
Из равенства векторов
и 
следует равенство их
координат:
, 
, 
,
ч.т.д.
Обратно,
пусть точка 
.
Тогда 
и
по теореме о коллинеарности векторов ни
один из них не может быть линейно выражен
через другой, т.е. 
и
хотя бы одно из равенств (7) не выполняется.
Таким образом, уравнениям (7)
удовлетворяют координатытолько
тех точек, которые лежат на прямой L и
только они, ч.т.д.
Теорема доказана.
Следствие. Следующая система уравнений является уравнениями прямой:
.
(8)
Доказательство. Выразив параметр t из уравнений (7), получаем:
, 
, 
,
(9)
откуда и следуют уравнения (8). Ясно, что системы уравнений (7) и (8) равносильны, т.е. их множества решений совпадают и система (8), так же как и система (7), являются уравнениями прямой, ч.т.д.
Следствие доказано.
Определение. Уравнения (8) называются каноническими уравнениями прямой.
8.