Використання складних умов

☻4.36. Перевірити, чи належить число, введене з клавіатури, інтервалу (-5; 3).

☻4.37. Визначити, чи потрапляє точка із заданими координатами в область I (див. мал.). Для простоти прийняти, що точка не потрапляє на кордон цієї області.

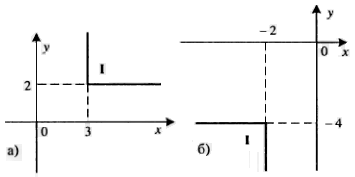
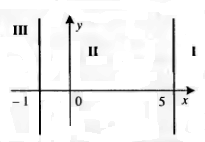
☻4.38. Визначити, чи потрапляє точка із заданими координатами в одну з областей I або III (див. мал.). Для простоти прийняти, що точка не потрапляє на кордон цих областей.

☻4.39. Дано дійсне число x. Обчислити f(x), якщо

☻4.40. Дане дійсне число х. Обчислити f(х), якщо

☻4.41. Дано три дійсні числа а, b, с. Перевірити: а) чи виконується нерівність а < b < c; б) чи виконується нерівність b>а>с.

☻4.42. Визначити, чи є число а дільником числа b або, навпаки, число b дільником числа а. Відповіддю повинні служити повідомлення "Так, одне з чисел є дільником іншого" чи "Ні, жодне з чисел не є дільником іншого".

☻4.43. Визначити, чи вірно, що при діленні невід'ємного цілого числа а на додатне число b виходить остача, рівна одному з двох заданих чисел c або d.

☻4.44. Дано три дійсні числа а, b, с. Визначити, чи є серед них хоч би одна пара рівних між собою чисел.

☻4.45. Визначити, чи є трикутник із сторонами а, b, c рівностороннім.

☻4.46. Визначити, чи є трикутник із сторонами а, b, c рівнобедреним.

☻4.47. Відомий зріст трьох чоловік. Визначити, чи однаковий у них зріст?

☻4.48. Дані дійсні числа а, b, c (а ≠ 0). Розв'язати рівняння аx² + bx + c = 0. У числі можливих варіантів врахувати варіант рівності коренів рівняння.

☻4.49. Дані дійсні додатні числа а, b, c, d. З'ясувати, чи можна прямокутник із сторонами а, b умістити усередині прямокутника із сторонами c, d так, щоб кожна із сторін одного прямокутника була паралельна або перпендикулярна кожній стороні другого прямокутника.

☻4.50. Дані дійсні додатні числа а, b, c, х, y. З'ясувати, чи пройде цеглина з ребрами а, b, c у прямокутний отвір із сторонами x і y. Просовувати цеглину в отвір дозволяється лише так, щоб кожне з його ребер було паралельне або перпендикулярне кожній із сторін отвору.

☻4.51. Дано двозначне число. Визначити: а) чи входить в нього цифра 3; б) чи входить в нього цифра а.

☻4.52. Дано двозначне число. Визначити: а) чи входять в нього цифри 4 або 7; б) чи входять в нього цифри 3, 6 або 9.

☻4.53. Дано тризначне число. Визначити: а) чи входить в нього цифра 6; б) чи входить в нього цифра а.

☻4.54. Дано тризначне число. Визначити: а) чи входять в нього цифри 4 або 7; б) чи входять в нього цифри 3, 6 або 9.

☻4.55. Дано чотиризначне число. Визначити: а) чи входить в нього цифра 4; б) чи входить в нього цифра b.

☻4.56. Дано чотиризначне число. Визначити: а) чи входять в нього цифри 2 або 7; б) чи входять в нього цифри 3, 6 або 9.

☻4.57.Дано натуральне число N (N<9999). З'ясувати, чи є воно паліндромом ("перевертнем") з врахуванням чотирьох цифр, як, наприклад, числа 7777, 8338, 0330 і тому подібне (паліндромом називається число, десятковий запис якого читається однаково зліва направо і справа наліво).

☻4.58.Дано натуральне число N (N<9999). З'ясувати, чи вірно, що це число містить рівно три однакові цифри з врахуванням чотирьох цифр, як, наприклад, числа 3363, 4844, 0300 і тому подібні.

☻4.59.Дано натуральне число N (N<9999). З'ясувати, чи різні всі чотири цифри цього числа (з врахуванням чотирьох цифр). Наприклад, в числі 3678 всіх цифр різні, в числі 0023 - ні.

☻4.60. Визначити, чи є задане шестизначне число щасливим. (Щасливим називають таке шестизначне число, сума перших трьох цифр якого дорівнює сумі його останніх трьох цифр.)

☻4.61. Рік є високосним, якщо його номер кратний 4, проте з кратних 100 високосними є лише кратні 400. Наприклад, 1700, 1800 і 1900 не високосні роки, 2000 - високосний. Дано натуральне число N. Визначити, чи є високосним рік з таким номером.

☻4.62. Є стіл прямокутної форми з розмірами а*b (а і b - цілі числа, а > b) і кості доміно з розмірами c*d*e (з, d і е - цілі числа, з > d >e). Знайти варіант розміщення на столі найбільшої кількості костей. Всі розміщувані кістки повинні лежати на одній і тій же грані в один ярус без звішування із столу. Всі ребра кісток доміно мають бути паралельні або перпендикулярні кожній стороні столу.

☻4.63. Дано ціле число K (1 < K < 365). Визначити, яким буде К-й день року: вихідним (субота і воскресіння) або робочим, якщо 1 січня - понеділок.

☻4.64. Траєкторія снаряду, що вилітає із гармати під кутом  з початковою швидкістю v_o, (див. мал.), задається рівняннями:

х = v_ot cos.

y = v_ot sin - gt²/2

де g = 9,8 м/с² - прискорення вільного падіння, t - час.

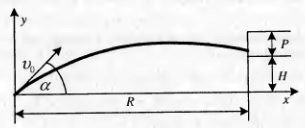
Дані значення  і v_о. Визначити, чи уразить снаряд ціль висотою Р, розташовану у вертикальній площині ствола гармати на відстані R на висоті H.

☻4.65. Дано два прямокутники, сторони яких паралельні або перпендикулярні осям координат. Відомі координати лівого нижнього кута кожного з них і довжини їх сторін. Один з прямокутників назвемо першим, інший - другим. а) Визначити, чи належать всі точки першого прямокутника другому; б) Визначити, чи належать всі точки одного з прямокутників іншому; в)* Визначити, чи перетинаються ці прямокутники.