Розділ 6. Інтегральне числення функції однієї змінної

Тема 1: Невизначений і визначений інтеграл. Властивості інтегралу. Таблиця інтегралів.

1. Невизначений інтеграл та його властивості. Таблиця невизначених інтегралів.

2. Визначений інтеграл, його властивості та обчислення.

Короткі теоретичні відомості

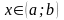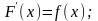
Функція F називається первісною для функції f на проміжку , якщо Якщо функція f має первісну F , то вона має нескінченну множину первісних, які містяться у виразі F+C, де C-стала.

Множина всіх первісних для функції f називається невизначеним інтегралом і позначається .

Властивості невизначених інтегралів:

1. 

2. .

3. 

4. 

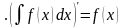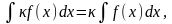
Таблиця основних інтегралів:

1. 

2. 

3. ,

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. .

14. .

15. 

16. .

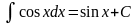
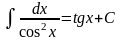
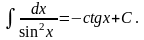
Одним з методів інтегрування є метод розкладу, який ґрунтується на застосуванні властивостей 2, 3 і табличних інтегралів.

Приклад. Обчислити інтеграл

Скориставшись властивостями 2,3 і табличними інтегралами 3, 2, дістанемо

Нехай функція y = f(x) визначена на відрізку [a;b] і - довільне розбиття цього відрізка на n-частини. Інтегральною умовою для функції f на [a;b] називається сума вигляду

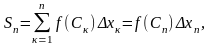(1)

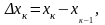
Ця сума має скінчену границю І, якщо

таке , що при , нерівність виконується при будь-якому виборі точок

Визначеним інтегралом від функції f на відрізку [a;b] називається границя інтегральної суми (1) за умови, що довжина найбільшого з елементарних відрізків прямує до нуля.

(2)

Числа a і b називаються відповідно нижньою і верхньою межами інтегрування. Функція f, для якої границя y правій частині рівності (2) існує (скінчена), називається інтегрованою на [a;b] зокрема, інтегрованими на відрізку [a;b] є функції : а)неперервна; б) обмежена, що має скінчене число точок розриву.

Основні властивості визначеного інтегралу:

1. 

2. .

3. .

4. .

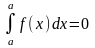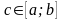Визначений інтеграл обчислюють за формулою Ньютона - Лейбніца:

(3)

де F - одна з первісних для f, тобто 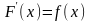на [a;b]

Приклад. Обчислити за формулою Ньютона - Лейбніца інтеграл .

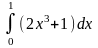Оскільки всі підінтегральні функції неперервні на відповідному відрізку, то застосовуючи формулу (3)і властивість 3,маємо

Питання для контролю вивченого матеріалу

1. Яка функція називається первісною для заданої функції?

2. Якщо F(x) - первісна для f(x), то якою рівністю пов’язані вони між собою?

3. Що називається невизначеним інтегралом?

4. Чим відрізняється невизначений інтеграл від первісної функції?

5. Чому інтеграл називається невизначеним?

6. Як називаються всі елементи рівності ?

7. Чим відрізняються один від одного підінтегральна функція та підінтегральний вираз?

8. Чому дорівнює похідна невизначеного інтегралу?

9. В чому полягає властивість інтегрування алгебраїчної суми функцій?

10. Запишіть основні формули інтегрування.

11. Що таке визначений інтеграл?

12. Що в запису 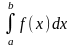означають: а) числа a, b; б) х; в) f(x); г) f(x)dx? Чи може бути a = b; a>b?

13. Сформулюйте основні властивості визначного інтегралу.

14. Обчисліть .