6.2 Случай несовершенной информации

Теперь мы переходим к более интересной ситуации, когда производители знают цены на свои товары, но не знают агрегированный уровень цен.

Поведение производителя

Обозначив через относительную цену товара , можно записать:

(6.16)

Таким образом, переменная, которую может наблюдать индивид – цена его товара – равна сумме относительной цены товара и агрегированного уровня цен (в логарифмах).

Принимаемые индивидуальные решения о производстве должны основываться только на (см. [6.6]). Однако индивид не наблюдает переменную и должен оценить ее на основании наблюдаемой переменной .⁴ Далее Лукас вводит два упрощающих предположения. Во-первых, он предполагает, что индивиды вначале строят свои ожидания относительно величины для данной величины , а затем выбирают такой объем производства, как если бы построенная оценка была детерминированной. Тогда уравнение (6.6) принимает вид:

. (6.17)

Как показывает задача 6.1, данное поведение, построенное по принципу эквивалентности детерминированному случаю, отличается от максимизации ожидаемой полезности: вообще говоря, выбор, максимизирующий ожидаемую полезность, зависит не только от оценки индивидом величины , но также и от того, насколько неопределенной он считает эту величину. Однако предположение о том, что индивиды используют принцип эквивалентности, не искажает основные результаты модели, упрощая при этом анализ.

Во-вторых, (и это очень важно) Лукас предполагает, что индивиды формируют ожидание при данном рациональным образом. Т.е., предполагается, что - это среднее значение , исчисляемое на основе информации о и о совместном распределении двух этих переменных^*. На сегодняшний день, предположение о рациональных ожиданиях кажется не менее привычным, чем предположение о максимизации индивидом функции полезности. Однако, в то время, когда Лукас ввел в макроэкономический анализ гипотезу рациональных ожиданий, предложенную в работах Muth (1960, 1961), она воспринималась как весьма спорная. Как мы увидим ниже, это один из источников (хотя и далеко не единственный) основных результатов модели Лукаса.

Чтобы упростить вычисления , монетарные шоки ( ) и шоки индивидуального спроса на товары ( ) полагаются нормально распределенными. Величина имеет среднее и дисперсию . Величины имеют нулевое среднее, дисперсию и полагаются независимыми от . Как мы увидим, из этих предположений следует, что величины и являются независимыми и нормально распределенными. Т.к. равна , эта величина также будет нормально распределенной со средним, равным сумме средних и , и дисперсией, равной сумме дисперсий этих переменных. Также мы увидим, что средние и , и , равны, соответственно, и 0, а их дисперсии и - это сложные функции от , и других параметров модели.

Задача индивида состоит в построении ожидания при данном . Один из важных результатов математической статистики состоит в том, что в случае, когда две переменных имеют совместное нормальное распределение (как и в данной ситуации), ожидание одной из переменных является линейной функцией от наблюдаемого значения второй. Таким образом, может быть представлено в виде:

. (6.18)

В данном частном случае, когда равно плюс независимая случайная величина, (6.18) принимает конкретную форму:

(6.19)

Смысл уравнения (6.19) понятен интуитивно. Во-первых, получается, что если совпадает со своим средним, то и ожидаемая величина будет равна своему среднему, т.е. 0. Во-вторых, ожидаемая величина превосходит среднее тогда, когда превосходит свое среднее, и оказывается ниже среднего, в ситуации, когда ниже среднего. В третьих, доля в отклонении от своего среднего, объясняемая отклонением от своего среднего, равна . И это есть не что иное, как доля общей дисперсии , равной , объясняемая дисперсией , т.е. . Так например, если равно 0, то вся вариация случайной величины обусловлена вариацией , так что равно . А если и равны, то половина дисперсии объясняется дисперсией , так что . И т.д.⁵

Подставляя (6.19) в (6.17), получаем индивидуальное предложение труда:

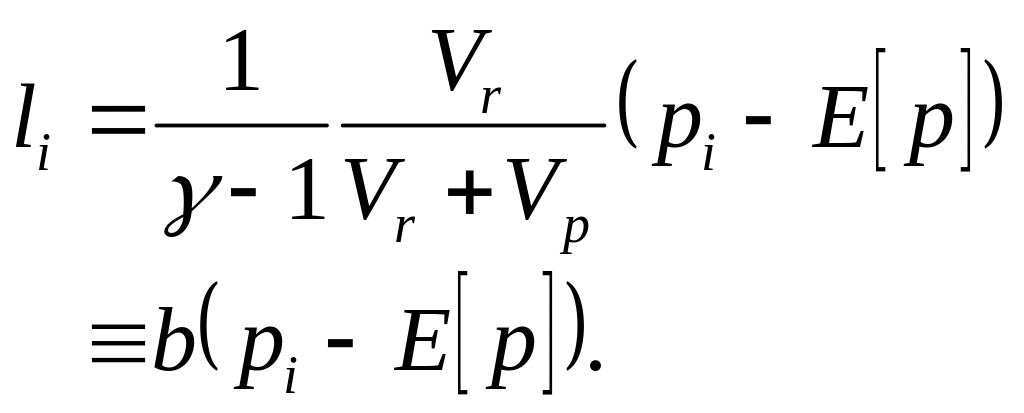(6.20)

Усредняя (6.20) по производителям и используя определения и , получаем выражение для агрегированного выпуска:

(6.21)

Уравнение (6.21) описывает кривую предложения Лукаса. В соответствии с ним, отклонение выпуска от своего нормального уровня (равного нулю в данной модели) является возрастающей функцией от неожиданного отклонения уровня цен.

Кривая предложения Лукаса, по существу, совпадает с представленной в главе 5 модифицированнойкривой Филлипса, где базовая инфляция заменена на инфляционные ожидания (см. уравнение [5.38]). Оба подхода предполагают, что если не брать в расчет шоки предложения, выпуск становится выше равновесного только в ситуации, когда инфляция (и, следовательно, уровень цен) выше ожидаемого уровня. Таким образом, модель Лукаса подводит микроэкономическое основание под данный взгляд на агрегированное предложение.