§4. Линейная зависимость и независимость векторов

Векторы называются линейно независимыми, если равенство

возможно лишь при , где - вектор все ко­ординаты которого равны нулю.

Векторы называются линейно зависимыми, если существуют числа не все одновременно равные нулю, для ко­торых имеет место равенство .

Пусть . Тогда, разделив это равенство на , и перенеся все век­торы, кроме , в правую часть, получим:

и, если обозначить отношение то

Это выражение и называется линейной комбинацией векторов.

Таким образом, если несколько векторов линейно зависимы, то хотя бы один из них можно представить в виде линей­ной комбинации остальных и наоборот, если один из векторов можно представить в виде линейной комбинации других векторов, то все эти векторы линейно зависимы.

Отметим, что любые три (или больше) вектора на плоскости ли­нейно зависимы.

Максимальное число линейно независимых векто­ров на плоскости равно двум. При этом не любые два вектора на плоскости будут линейно независимы.

Так в случае коллинеарностивекторов вектор является линейной комбинацией и, следовательно, они линейно зависимы.

Аналогично в трехмерном пространстве максимальное число ли­нейно независимых векторов равно 3.

Введем понятие базиса на плоскости и в пространстве.

Базисом на плоскости называются любые два линейно независимых вектора.

Таким образом, если любые два вектора плоскости и неколлинеарны, то они образуют базис, а любой вектор уже не может быть линейно независим от них, следовательно, является их линейной комбинацией: где числа координаты вектора в базисе , .

Аналогично, в трехмерном пространстве, базисом называются лю­бые три линейно независимых вектора.

Вектора называются компланарными, если они параллельны од­ной плоскости или лежат в одной плоскости.

Следовательно, всякие три не компланарные вектора образуют базис.

Вспомним теперь введенные раньше орты . Так как они не компланарны, то образуют базис, который называется ортонормированным базисом или декартовой системой координат в простран­стве.

Пример: Образуют ли векторы , , базис? Если образуют, найти координаты вектора в этом базисе. Даны векторы

.

Определить являются ли векторы , , линейно независимыми?

Эти вектора будут линейно независимы если являются некомпланарными, т.е. определитель системы, составленной из координат этих векторов должен быть отличен от нуля:

Видим, что , следовательно, векторы , , составляют ба­зис.

Найдем координаты вектора в базисе , , . Четыре вектора в трехмерном пространстве всегда линейно зависимы (т.е. вектор есть линейная комбинация векторов , , ).

,

В нашем случае

Решим эту систему линейных уравнений методом Крамера.

(проверьте самостоятельно)

(проверьте самостоятельно).

Найдем значения неизвестных:

Получим коэффициенты разложения вектора по базису , ,

§5. Скалярное, векторное и смешанное произведения векторов

С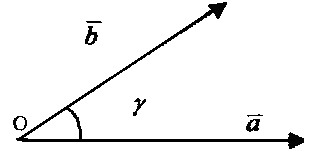 калярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

и обозначается .

Свойства скалярного произведения векторов:

1. ;

2. (ортогональность двух ненулевых векторов)

3. (переместительный закон)

4. (распределительный закон)

5. (сочетательный закон по отношению к скалярному множителю)

Скалярные произведения ортов осей координат:

Пусть векторы заданы своими координатами:

Тогда скалярное произведение этих векторов определяется формулой:

Используя скалярное произведение векторов, можно найти угол между ними:

Например, угол между векторами (1,2,0) и (2,3,5) имеет косинус

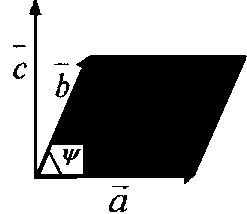Векторным произведением вектора на называется третий вектор (см. рисунок), определяемый следующим образом:

- модуль вектора равен площади параллелограмма, построенного на векторах ( , где - угол между векторами );

- вектор перпендикулярен векторам ;

- векторы , , образуют правую тройку.

Векторное произведение на обозначается