Вопросы и упражнения для самоконтроля:

1. Что такоечисловая матрица?

2. Что означают числа в индексе для элементов матрицы?

3. Что означает запись «размер матрицы (2 х 4)»?

4. Можно ли сложить матрицы А_{(2 х 3)} и В_{(3 х 4)}?

5. Какая матрица называется квадратной?

6. Что такое нуль-матрица?

7. Можно ли перемножить матрицыA= В=

8. Можно ли перемножить матрицы А_{(3 х 4)} и В_{(4 х 2)}?

9. Приведите пример единичной матрицы какой-либо размерно­сти.

§2. Определители

Каждой квадратной матрице А соответствует число - определи­тель данной матрицы (det А).

A= - определитель второго порядка.

B= - определитель третьего порядка

Для вычисления определителя второго порядка используют формулу:

A= =

Пример:

1) А=(а₁₁) матрица 1-ого порядка

₁= а₁₁= а₁₁, 7=7,  -3=-3

2) А= матрица 2-ого порядка

₂=

Определителем третьего порядка называют число, обозначаемое символом

и определяемое равенством

= (2)

Определитель 3-его порядка можно вычислить по правилу треугольника, схеме Саррюса.

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком«—», полезно использован следующее правило треугольников:

«+» «-»

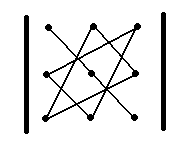
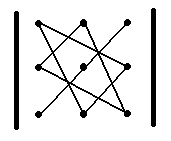
Это правило позволяет легко записать формулу (2) и вычислить дан­ный определитель.

А= матрица 3-его порядка

Правило треугольника:

₃=

Пример:

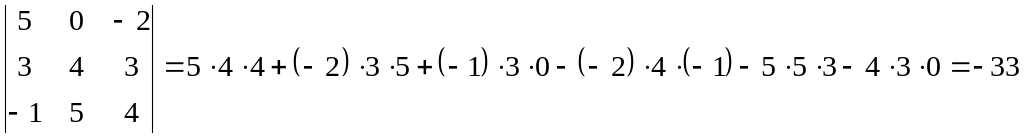
Минором М_ij элемента а_ij квадратной матрицы n-ого порядка называется определитель n-1 порядка, полученного путем вычеркивания из исходного определителяi-ой строки иj-ого столбца.

Пример:

А= М₁₃= М₂₂= М₃₂=

Алгебраическим дополнением A_ij элемента a_ij квадратной матрицы n-ого порядка называется его минор, взятый со знаком (-1)^i+j.

A_ij=(-1)^i+jM_ij.

Например, если элемент а₁₂ находится на пересечении первой строки и второго столбца, то для него р=1+2=3 и его алгебраическим дополнением является

A₁₂=(— 1)³ = - ( )

Пример:

А= А₁₃=(-1)¹⁺³ А₂₂=(-1)²⁺²М₂₂=120=20

Теорема Лапласа

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

=а_i1A_i1+a_i2A_i2+…+a_inA_in= .

Например, разложение определителя третьего порядка по элемен­там первой строки записывается так:

=

Значение теоремы разложения состоит в том, что позволяет свести вычисление определителей n-го порядка к вычислению определите­лей (n-1)-го порядка.

Пример: Вычислить определитель:

Решение:

Для вычисления данного определителя воспользуемся теоремой Лапласа: Определитель квадратной матрицы равен сумме произведений элементов, какой либо строки (столбца) на их алгебраические дополнения. Для более удобного вычисления выполним элементарные преобразования: умножим элементы 1-ой строки на 1, (-2), (-1), и прибавляя их соответственно к элементам 2-ой, 3-ей, 4-ой строк, добиваемся того, чтобы все элементы 3-его столбца(кроме а₁₃) равнялись нулю и разложим определитель по элементам 3-его столбца:

Для вычисления последнего определителя воспользовались правилом треугольника.

Ответ: определитель матрицы равен - 9.

Пример: Вычислить определитель:

Решение: Раскладывая определитель по элементам первой строки, получаем:

=1(-1)² +2(-1)³ +3(-1)⁴ =1 (1*2 - 0*1) - 2(0*2 - 0*2) + 3(0*1 - 2*1)= - 4

Ответ: =-4

Пример: Вычислить определитель самостоятельно:

Ответ: =-2