В.Д. Павлидис

Лекции по алгебре и аналитической геометрии

Оренбург 2011

ББК 22.12

УДК 517.51

Рецензенты:

Прояева И.В. - кандидат физико-математических наук, доцент кафедры «Геометрия» ОГПУ

Тычинина С.Е. - кандидат физико-математических наук, доцент кафедры естественно-математических дисциплин ОГИМ

Павлидис В.Д.

Лекции по алгебре и аналитической геометрии. – Оренбург: Издательский центр ОГАУ, 2011

Данный курс лекций предназначен для студентов-бакалавров 1 курса направления «Информатика и вычислительная техника», «Безопасность автоматизированных систем», «Агроинженерия». Пособие содержит весь необходимый материал по данному разделу математики, предусмотренный государственным образовательным стандартом для указанных направлений обучения бакалавров, снабжено богатым набором иллюстраций и примерами. Оно может быть использовано как для аудиторных занятий, так и для самостоятельной работы студентов.

Содержание

Элементы теории матриц и определителей………………………………...4

§1. Матрицы и их свойства…………………………………………..…………4

§2. Определители…………………………………………………….…………12

§3. Системы линейных уравнений……………………………….…………...18

§4. Ранг матрицы……………………………………………………………....27

Элементы векторной алгебры…………………………………..………..…31

§1. Арифметические действия над векторами…………………………….…31

§2. Векторное пространство…………………………………………………..32

§3. Декартова система координат…………………………………………….35

§4. Линейная зависимость и независимость векторов………………………37

§5. Скалярное, векторное и смешанное произведения векторов…………..40

Элементы аналитической геометрии ……………….………….................46

§1. Прямая на плоскости………………………………………………………46

§2. Плоскость…………………………………………………………………...…....50

§3. Прямая и плоскость в пространстве…………………………….…….….52

§4. Кривые второго порядка……………………………………….………....54

Литература…………………………………………………………….……....59

Элементы теории матриц и определителей

§ 1 Матрицы и их свойства

Матрицей называют таблицу, состоящую из n строк и m столбцов. Элементами матрицы могут быть числа или иные математиче­ские объекты.

A= B= C=

Прямоугольная таблица, содержащая т строкип столбцов действительных чисел называется числовой матрицей.

А_mn= .

Сокращенно А_mn= (a_ij). Далее будем рассматривать числовые матрицы.

Числа а_ij, составляющие матрицу, называются ее элементами, где i=1,2,…m номер строки, j=1,2,…n номер столбца.

Матрицы обозначается заглавными буквами латинского алфавита А, В, С…, элементы строчными буквами.

Если число строк и столбцов одной матрицы равно числу строк и столбцов другой матрицы, то они называются одноразмерными матрицами.

Виды матриц

Матрица, у которой число строк равно числу столбцов, называется квадратной матрицей. Квадратную матрицу размером nn называют матрицей n-ого порядка.

А_22= - квадратная матрица 2-ого порядка

а₁₁, а₂₂ элементы главной диагонали

а_12, а₂₁ элементы побочной диагонали

А_33=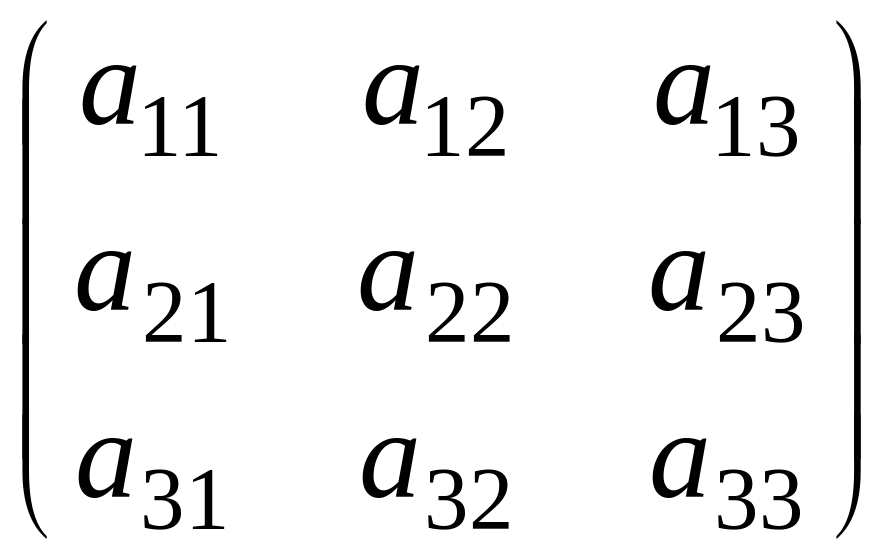 квадратная матрица 3-его порядка

а₁₁, а₂₂, а₃₃ элементы главной диагонали

а_13, а₂₂, а₃₁ элементы побочной диагонали

Квадратная матрица, все элементы которой, стоящие выше (ниже) главной диагонали равны нулю, называется треугольной матрицей.

Квадратная матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной матрицей.

В=

Диагональная матрица, все ненулевые элементы которой равны между собой, называется скалярной матрицей.

Диагональная матрица, все ненулевые элементы которой равны 1, называется единичной матрицей.

Е= единичная матрица 3-его порядка

Матрица, все элементы которой равны нулю, называется нулевой матрицей (0).

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор- столбец, или вектор-строка соответственно).

А= ; В=

Матрица размера 11, состоящая из одного числа, отождествляется с этим числом, т. е.(5)_11 есть 5.

Одноразмерные матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Квадратная матрица А^-1 называется обратной по отношению к матрице А. тогда и только тогда, когда А*А^-1=А^-1*А=Е