§ 2. Случайные события

Под испытанием понимается реализация какого-либо эксперимента, наблюдения, которые могут производиться неограниченное число раз. При этом эксперимент включает в себя случайные факторы, влияние которых в каждом испытании приводит к неоднозначности исхода испытания. Целью испытаний является получение тех или иных результатов.

Событиями называются возможные исходы испытаний. Обозначаются события: A, B, C и т.д. На основе различных признаков события можно классифицировать следующим образом:

по возможности появления:

• достоверные

• невозможные

• случайные

по совместности появления:

• совместные (происходят одновременно)

• несовместные (происходят не одновременно)

по взаимозависимости:

• зависимые (возможность появления одного зависит от наступления другого)

• независимые (возможность появления одного не зависит от наступления или отсутствия другого события);

по сложности:

• элементарные события - возможные, исключающие друг друга результаты одного испытания

• сложные события, состоящие из других событий.

Полной группой событий называют совокупность событий, из которых хотя бы одно должно произойти.

Противоположными называются два несовместных события образующих полную группу событий. Обозначаются: .

Элементарным событием называется конкретный результат испытания. В результате испытания происходят только элементарные события.

Пространством элементарных событий называется совокупность всех возможных, различных, конкретных исходов испытаний.

Количественное описание правдоподобия отдельных исходов и событий основывается на понятии вероятности.

Вероятностью события А называется отношение числа m равновозможных элементарных событий, благоприятствующих событию А к числу n всех возможных элементарных событий, образующих полную группу:

,

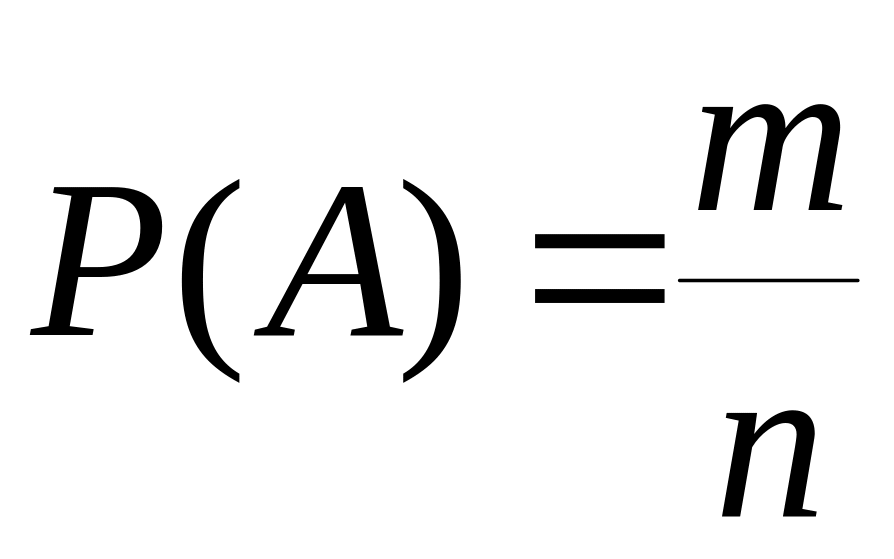где n – общее число равновозможных событий, а m – число тех событий, при которых происходит интересующий исход.

Это классическое определение вероятности дано Полем Лапласом.

Вероятность можно также определить как предел частости при бесконечно большом числе испытаний. Иными словами частота (частость) приблизительно равна вероятности, если число испытаний очень велико. Это определение вероятности называется статистическим.

Пример. Пусть следует вычислить вероятность события А - «при бросании двух костей выпало 8 очков».

Решение. При бросании двух костей могут получиться следующие равновозможные результаты:

I II	I II	I II	I II	I II	I II
1 1	2 1	3 1	4 1	5 1	6 1
1 2	2 2	3 2	4 2	5 2	6 2
1 3	2 3	3 3	4 3	5 3	6 3
1 4	2 4	3 4	4 4	5 4	6 4
1 5	2 5	3 5	4 5	5 5	6 5
1 6	2 6	3 6	4 6	5 6	6 6

Как видно, всего возможных результатов 36. Подчеркнем те случаи, когда произошло событие А. Таких случаев 5 - все они равновозможны. Таким образом, получаем: .

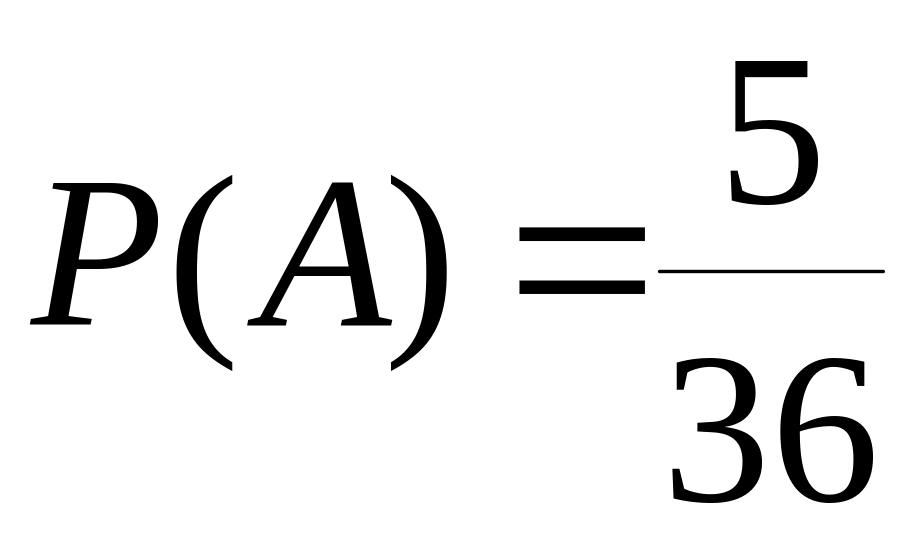Пример. Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4 бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди выбранных ламп будут 2 бракованные?

Решение. Прежде всего отметим, что выбор любой пятерки ламп имеет одну и ту же вероятность. Всего существует способов составить такую пятерку, то есть случайный эксперимент в данном случае имеет равновероятных исходов.

Каждую интересующую нас пятерку можно составить так: выбрать две бракованные лампы, что можно сделать числом способов, равным . Каждая пара бракованных ламп может встретиться столько раз, сколькими способами ее можно дополнить тремя не бракованными лампами, то есть раз. Получается, что число пятерок, содержащих две бракованные лампы, равно  .

Отсюда, обозначив искомую вероятность через P, получаем:

.

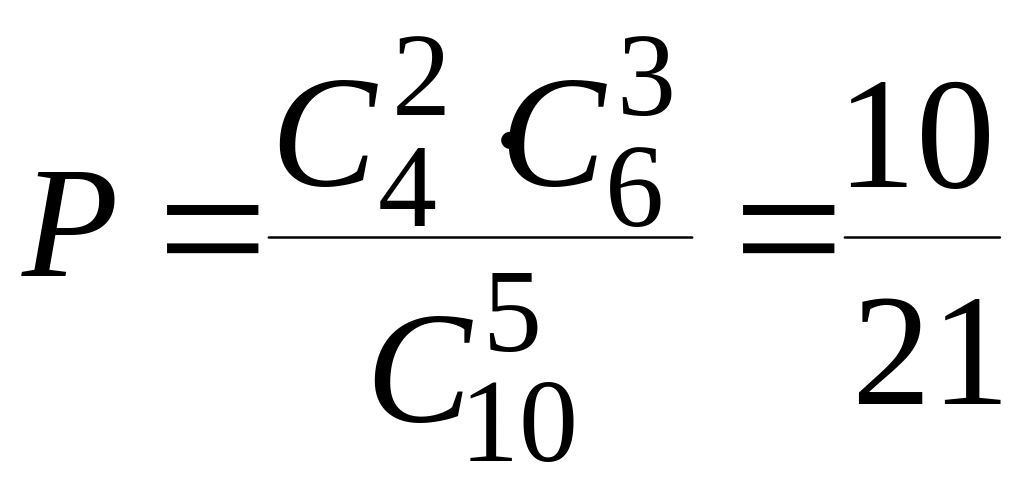Приведем свойства вероятности события: