1 2.6 Вольт-амперная характеристика искрового разряда

Рассмотрим вакуумный диод с острийным иди плоским катодом на котором функционирует одиночный КФ. Соотношений, описывающих вольт-амперную характеристику таких диодов, не известно. Будем полагать что плазма КФ находится под потенциалом катода, имеет сферическую эмиттирующую поверхность с неограниченной эмиссионной способностью. Качественно ясно, что при ограниченной эмиссионной поверхности катода объемный заряд электронов будет слабее возмущать потенциал любой точки межэлектродного пространства, чем при неограниченной. Это должно привести к увеличению предельной плотности тока в вакуумном промежутке. Будем использовать приближенный расчет плотности тока в диоде с бесконечными плоскопараллельными электродами для случая, когда неограниченной эмиссионной способностью обладает небольшой участок катода радиусом r, а радиальное расталкивание пучка объемным зарядом отсутствует. Чем меньше отношение r/d, тем больше ₀ = j_r/j_ ( j_r  истинная плотность тока, j_  плотность тока из закона Ленгмюра для бесконечных плоских электродов).

Воспользовавшись таким подходом и представляя площадь эмиссии электронов в виде 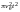, а расстояние между фронтом плазмы и анодом через , можно записать:

(12.12)

где А₁ = 2,3310_6 А/В_3/2. Из (12.12) следует, что первеанс электронного потока Р = = i(t)/ должен быть однозначной функцией отношения . Для проверки справедливости этого вывода было обработано большое количество осциллограмм тока в устойчивой стадии эмиссии, полученных с хорошим амплитудным и временным разрешением в диапазоне экспериментальных условий: d = 14 мм, U₀ = 2040 кВ и d = 610 мм, U₀ = 80120 кВ; катод  игла. Некоторые из экспериментальных точек, произвольно выбранные из большого количества (~300), приведены на рис. 12.3, а (кривая 1). Здесь принята скорость v_к = 210₆ см/с. Можно видеть, что большинство точек ложится на одну плавную кривую. Это же в полной мере относится и ко всем другим обработанным данным, не нанесенным на график для значений . На этом же рисунке дана зависимость P( ) для ₀ = 1 (кривая 2). Нетрудно видеть, что применение закона «степени 3/2», не учитывающего ограниченности эмиссионной поверхности, дает заниженные на один-два порядка значения электронного тока.

Для системы с плоскими электродами и одиночным КФ, возникшим на месте искусственно созданного микровыступа (U₀ = 2040 кВ, d = 0,31,0 мм), экспериментальные точки лучше всего укладывались на одну кривую Р = f(v_кt/d) (рис. 12.3, б).

Рис. 12.3. Зависимости первеанса электронного потока от отношения v_кt/(d  v_кt) для случая факела на острийном катоде (а) и от отношения v_кt/d для случая факела на плоском катоде (б). а  1  эксперимент; 2  расчет для плоского случая; 3  расчет по (12.3);. б  точки  эксперимент; сплошная линия  расчет.

Выражение, подобное (12.12), было получено аналитически. Плотность тока в каждой точке эмиттирующей сферической поверхности определялась, пользуясь известной формулой БогуславскогоЛенгмюра (11.29). Длина эффективного промежутка (эффективную длину траектории электрона выходящего из данной точки эмиттирующей поверхности) можно определялась из выражения d_эфф = U/E, где Е  напряженность электрического поля в данной точке сферы в отсутствие объемного заряда электронов. Следовательно, задача сводится к нахождению напряженности электростатического поля на катоде в произвольной системе электродов. Затем полный ток в промежутке определяется путем интегрирования плотности тока по эмиттирующей поверхности. Для случая, когда КФ функционирует на вершине острия получено:

. (12.3)

Зависимость (12.3) представлена на рис. 12.3, а (линия 3). Она удовлетворительно согласуется с экспериментальными результатами. При этом ₀  5 .

Для случая полусферической эмиттирующей поверхности на плоском катоде аналогичным образом получено:

. (12.4)

Эта зависимость показана на рис. 12.3 б и также хорошо согласуется с экспериментальными данными при ₀  6.

Заметим, что поскольку напряженность электрического поля в эффективном диоде находилась из выражений, справедливых при условии v_кt  d, то и соотношения (12.3) и (12.4) можно использовать только при выполнении этого условия.