Южно-Уральский Государственный Университет
Международный факультет
Кафедра «Общеобразовательные дисциплины»
Семестровая работа № 1 по курсу
«Математика»
для студентов дневного отделения
специальность «Управление персоналом»
Преподаватель: Кунгурцева Алла Васильевна
Срок сдачи: до 17.12.2012
Челябинск
2012
I. Вычислить определитель:
а) разложив его по элементам i-ой строки;
б) разложив его по элементам j-го столбца;
Варианты:
1)
,
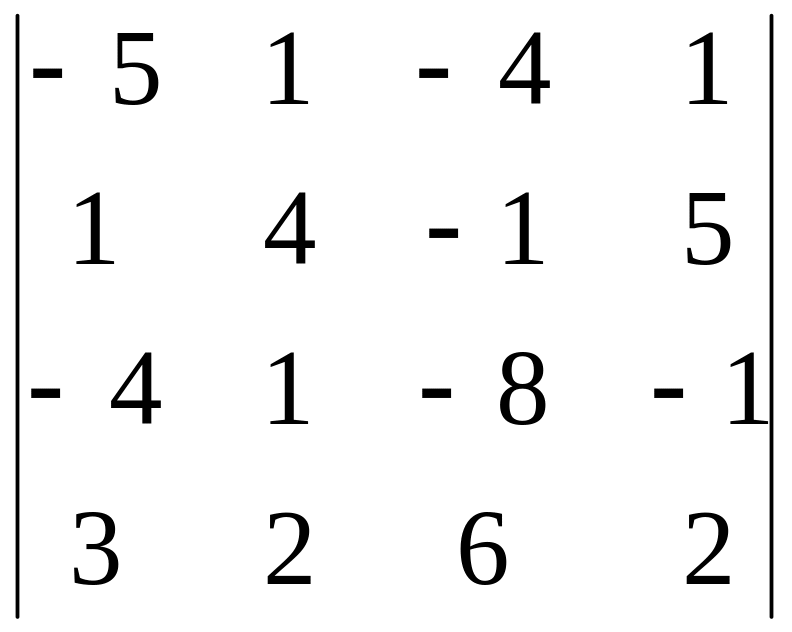i=2, j=3;
2)
,
i=3, j=1;
3)
,
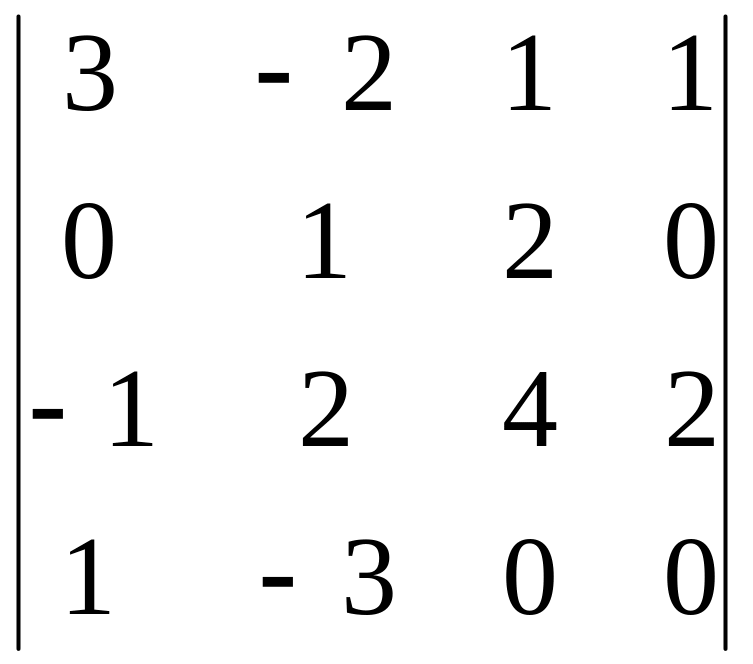i=3, j=2;
4)
,
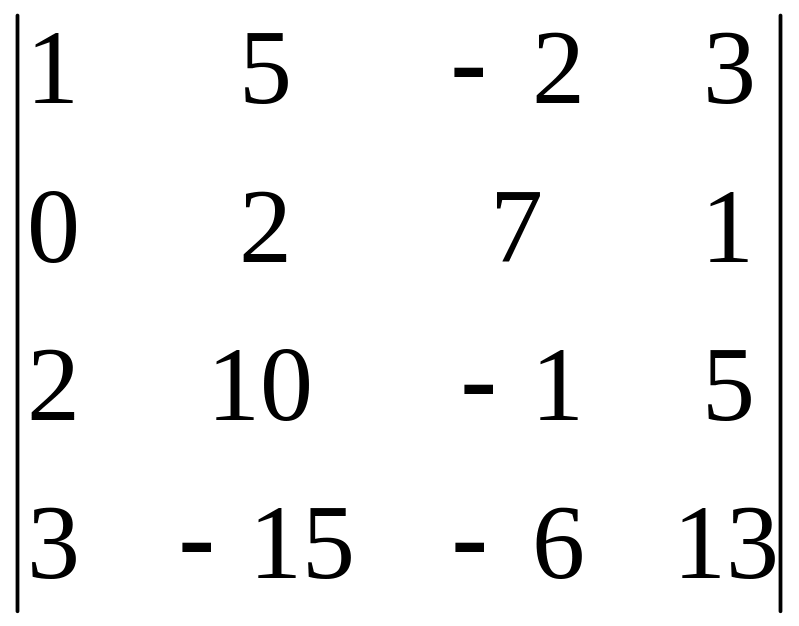i=2, j=4;
5)
,
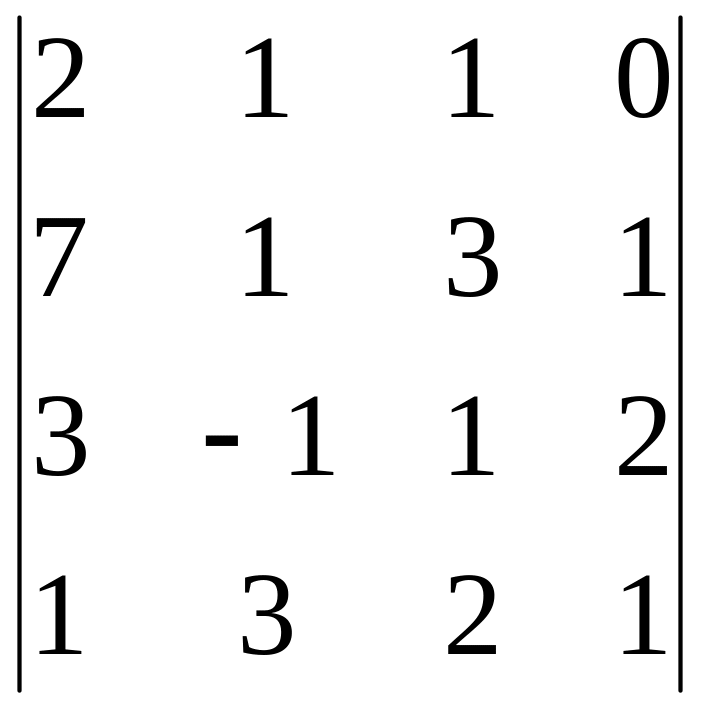i=4, j=2;
6)
,
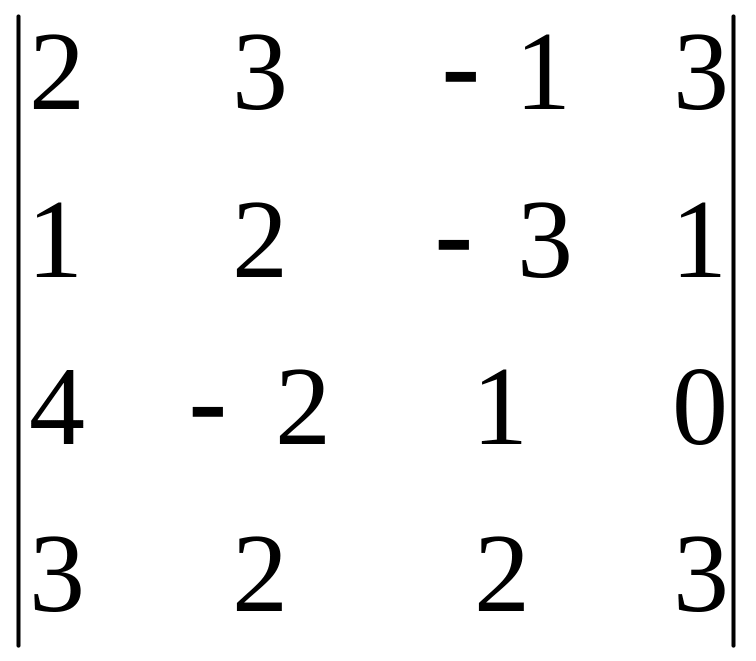i=2, j=1;
7)
,
i=3, j=3;
8)
,
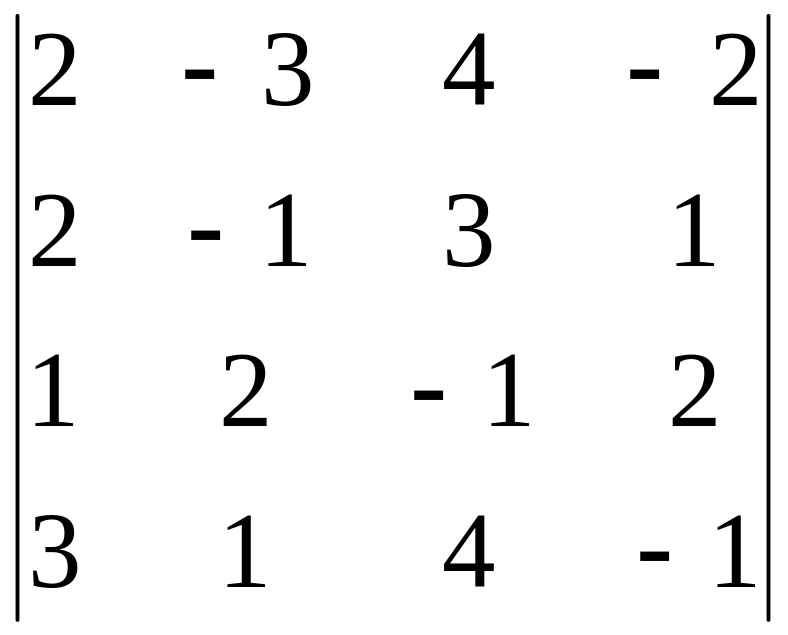i=3, j=4;
9)
,
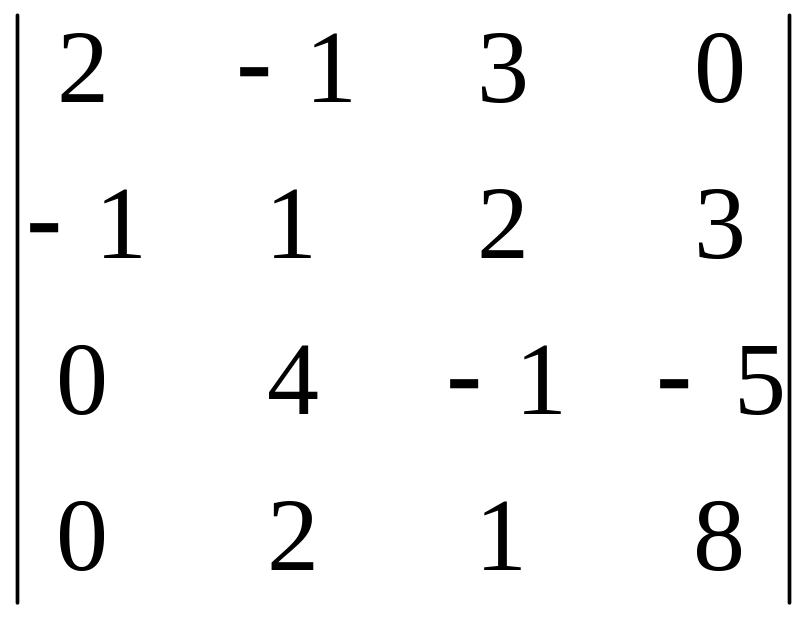i=1, j=2;
10)
,
i=2, j=1;
11)
,
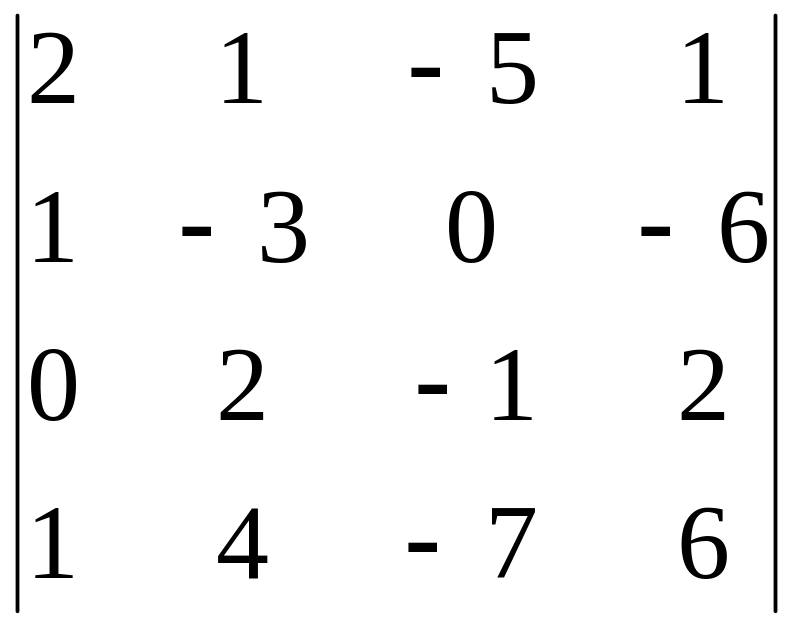i=4, j=3;
12)
,
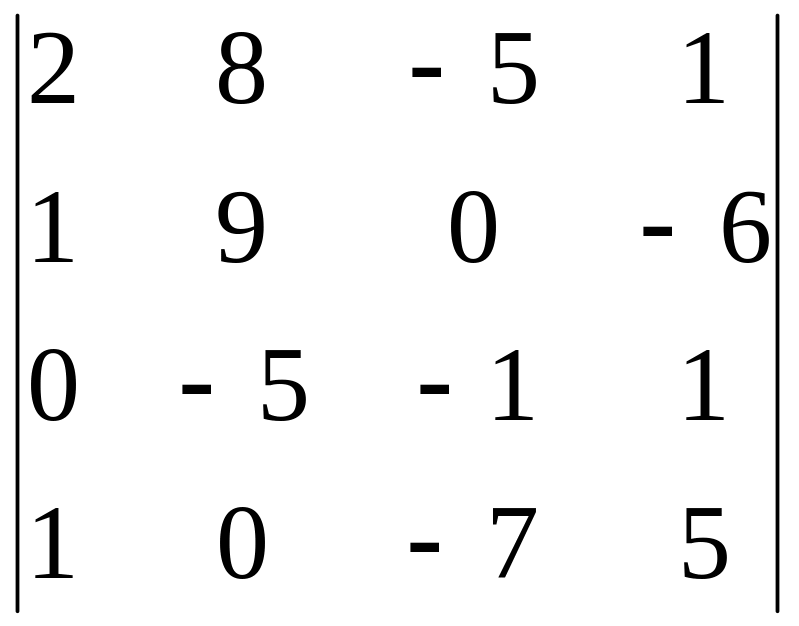i=3, j=1;
13)
,
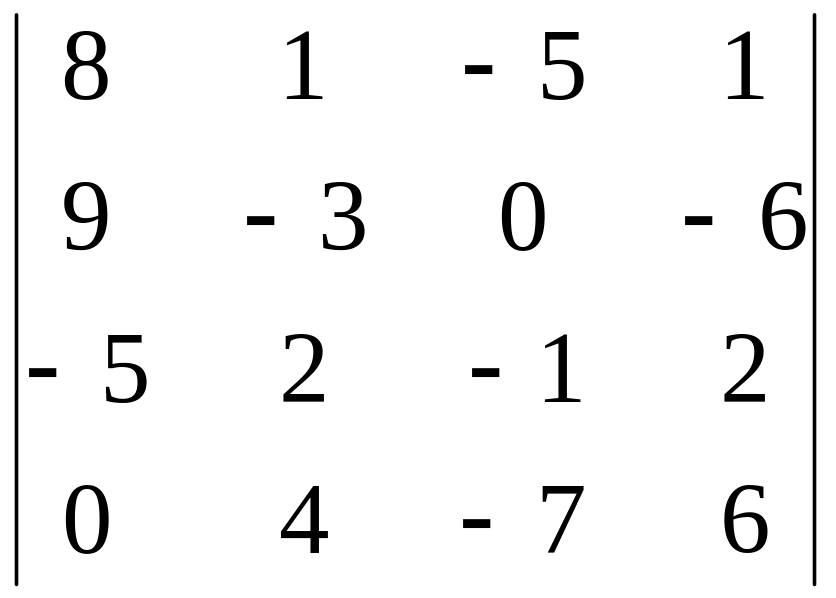i=1, j=4;
14)
,
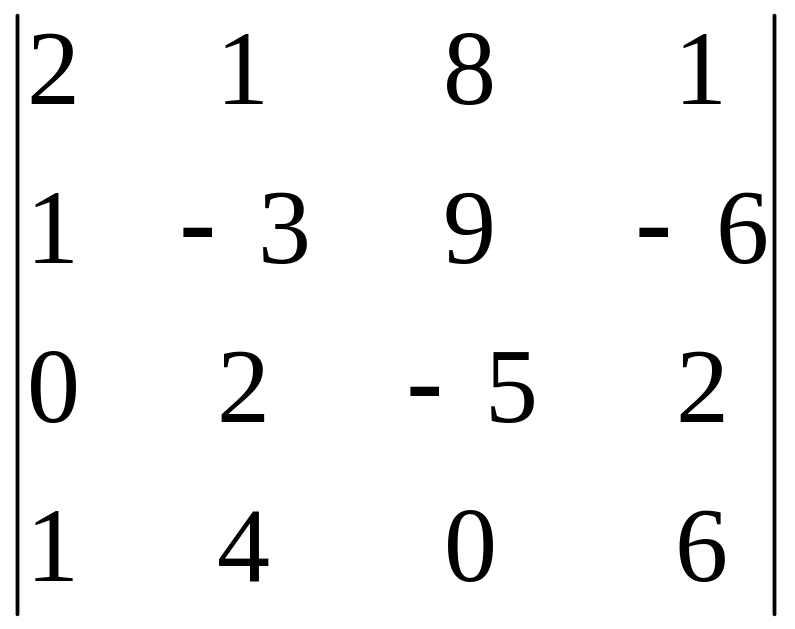i=2, j=2;
15)
,
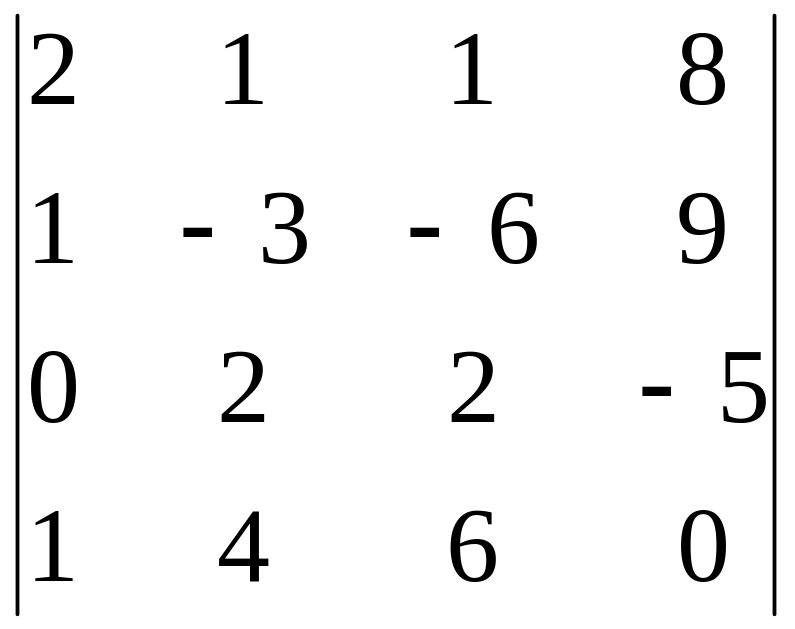i=4, j=3;
16)
,
i=1, j=2;
17)
,
i=3, j=2;
18)
,
i=4, j=4;
19)
,
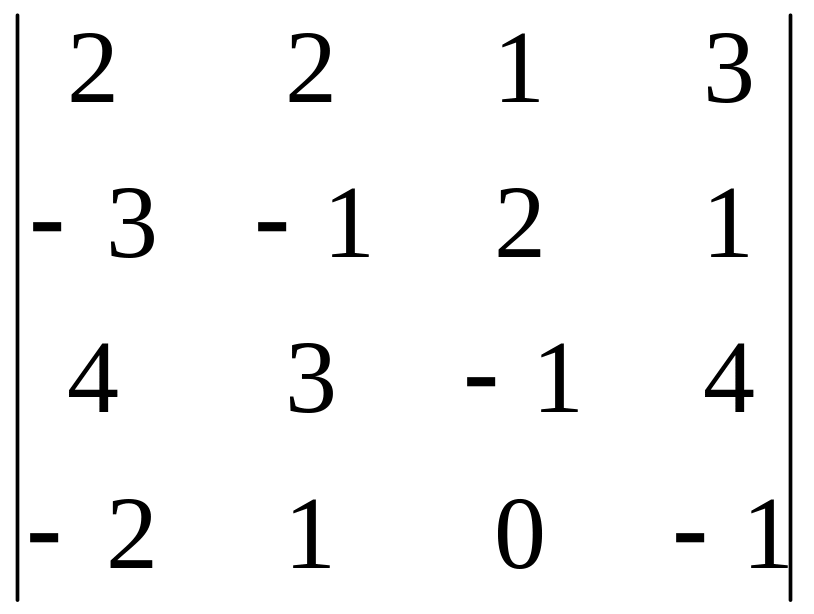i=2, j=3;
20)
,
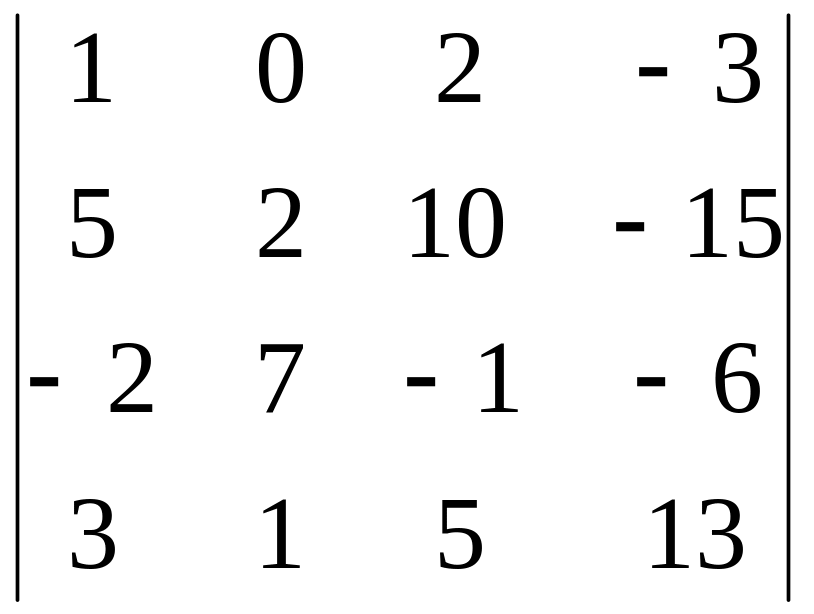i=1, j=1;
21)
,
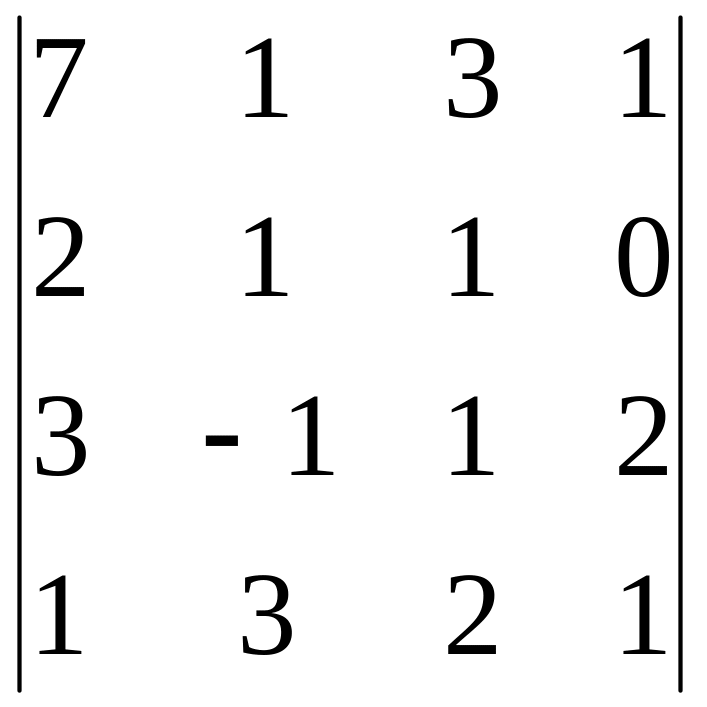i=3, j=2;
22)
,
i=4, j=3;
23)
,
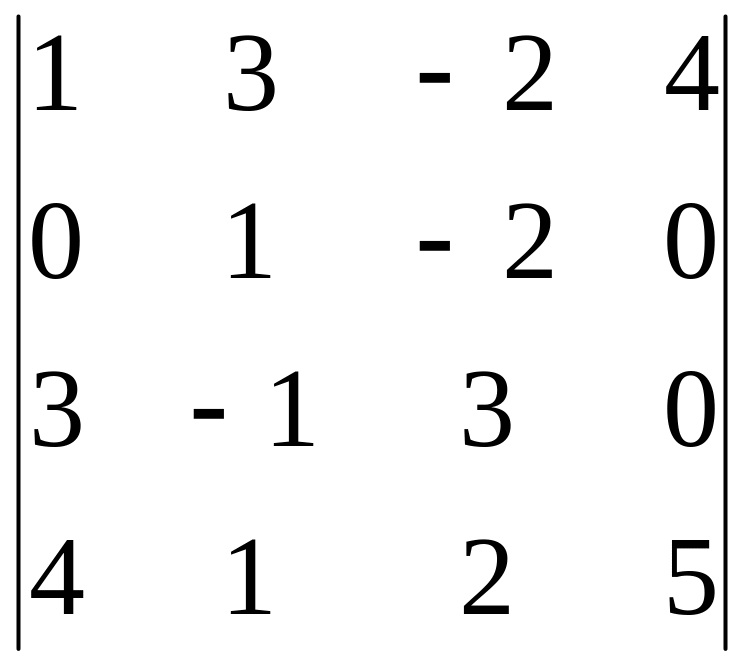i=2, j=2;
24)
,
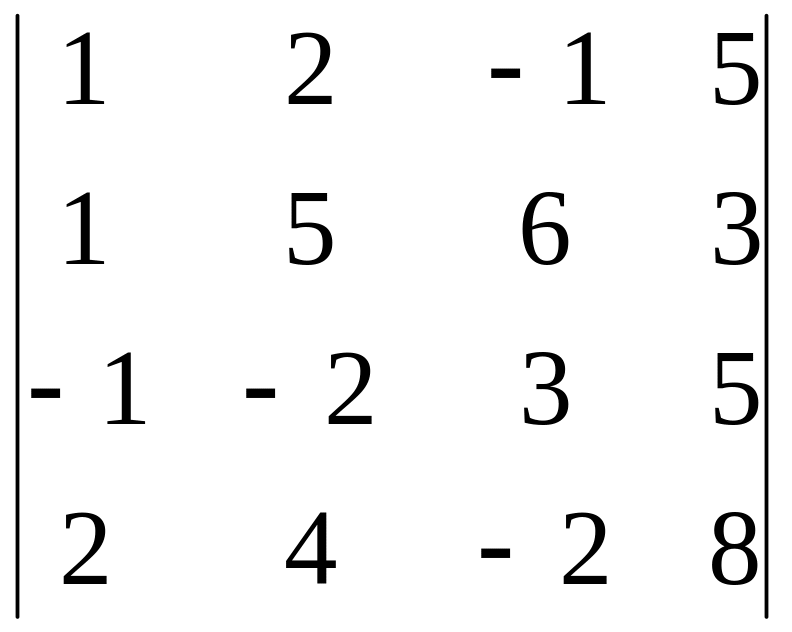i=3, j=3;
25)
,
i=1, j=4;
26)
,
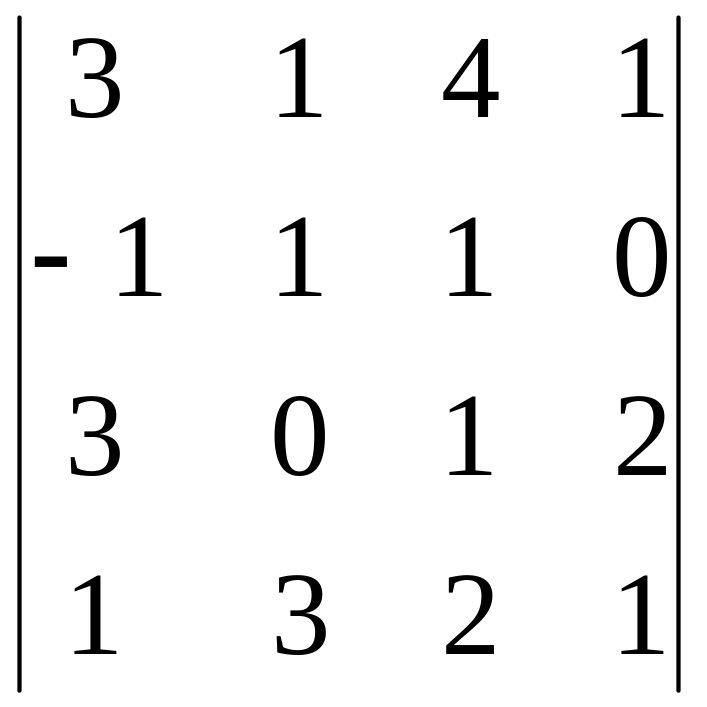i=4, j=1;
27)
,
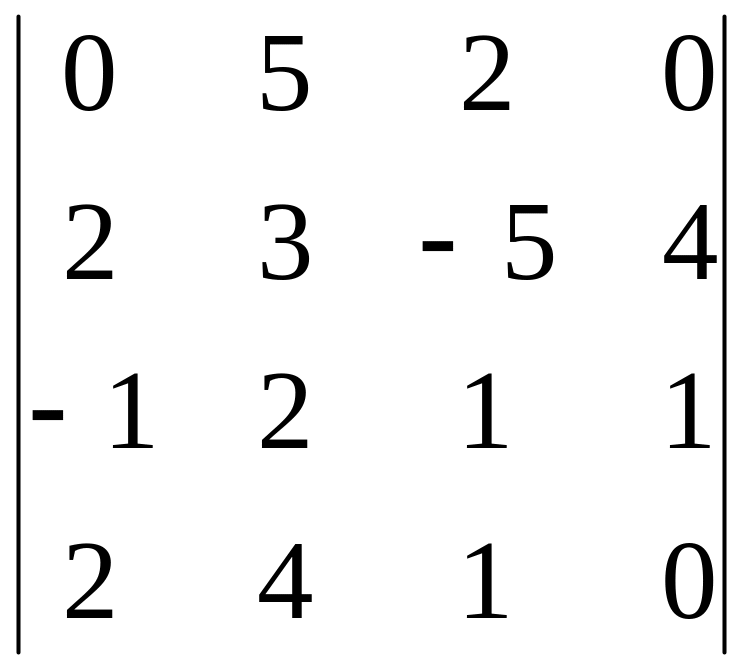i=3, j=3;
28)
,
i=2, j=1;
29)
,
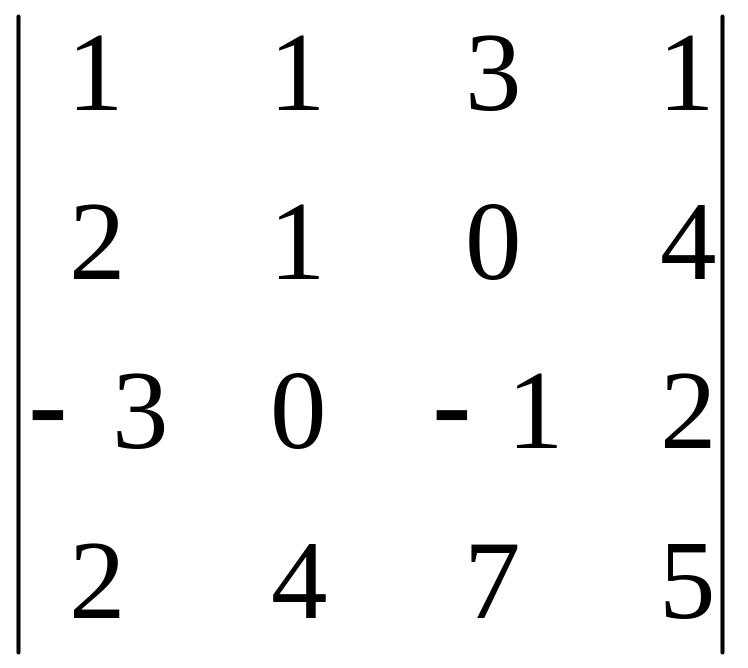i=3,
j=4;
30)
,
i=4,
j=2;
II. Выполнив действия над матрицами, найти матрицу к.
Варианты:
1)
,
,
,
,
;
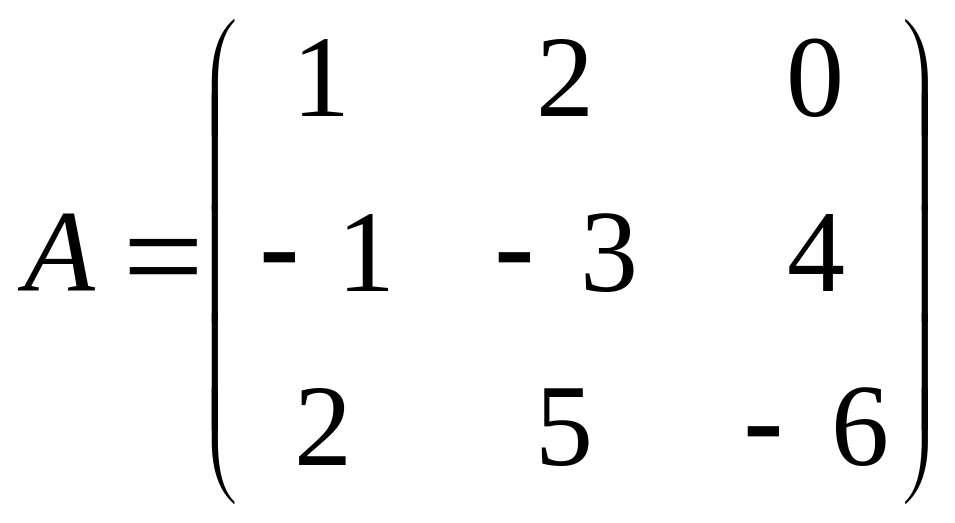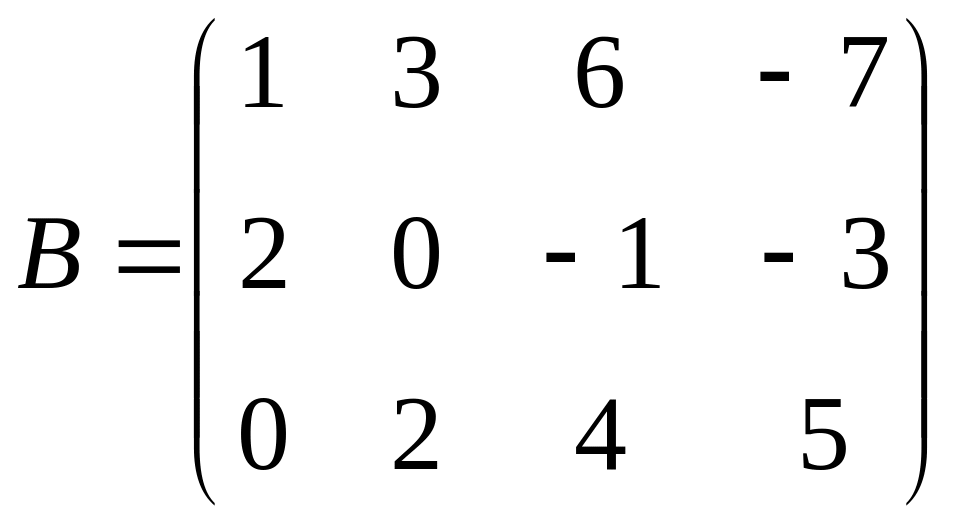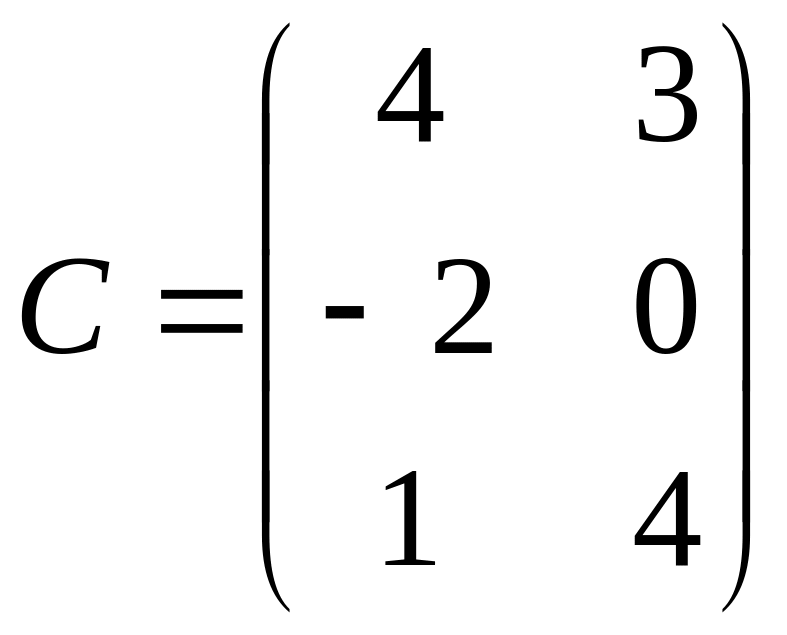2)
,
,
,
,
;
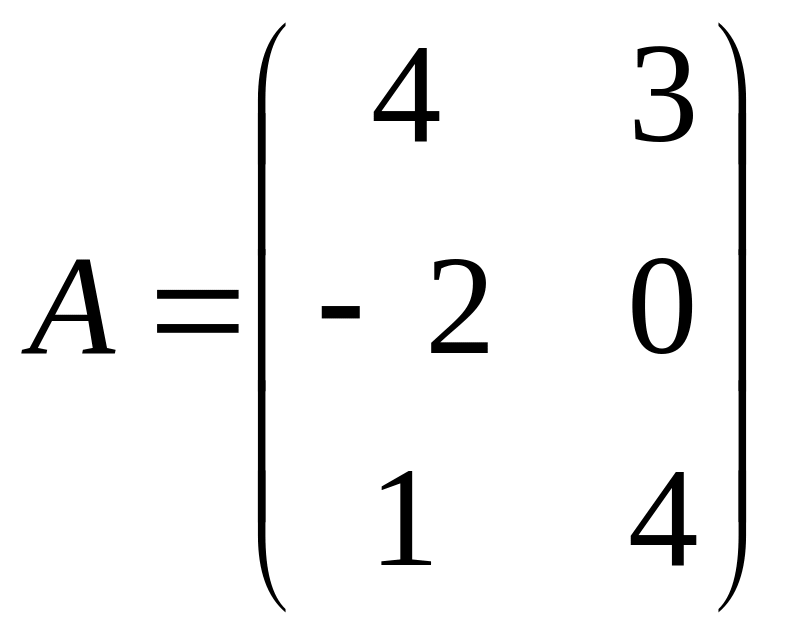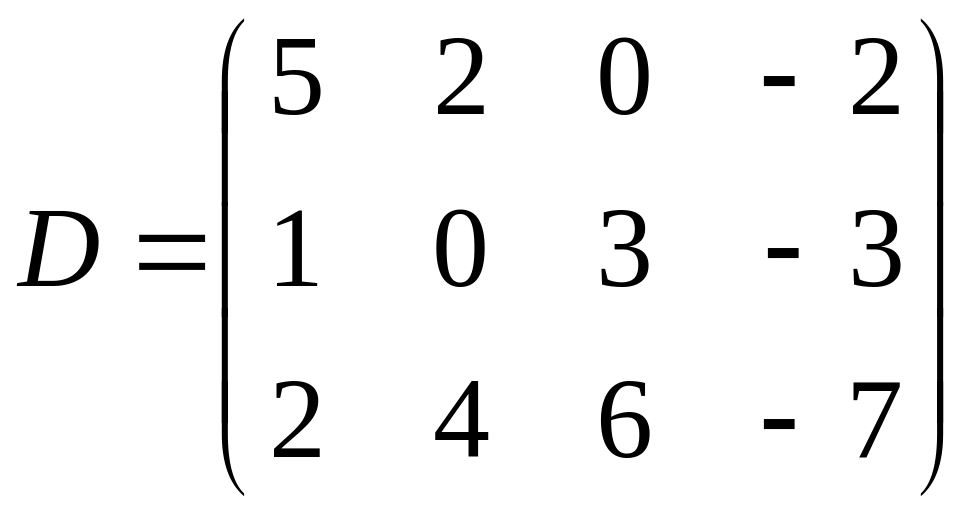3)
,
,
,
,
;
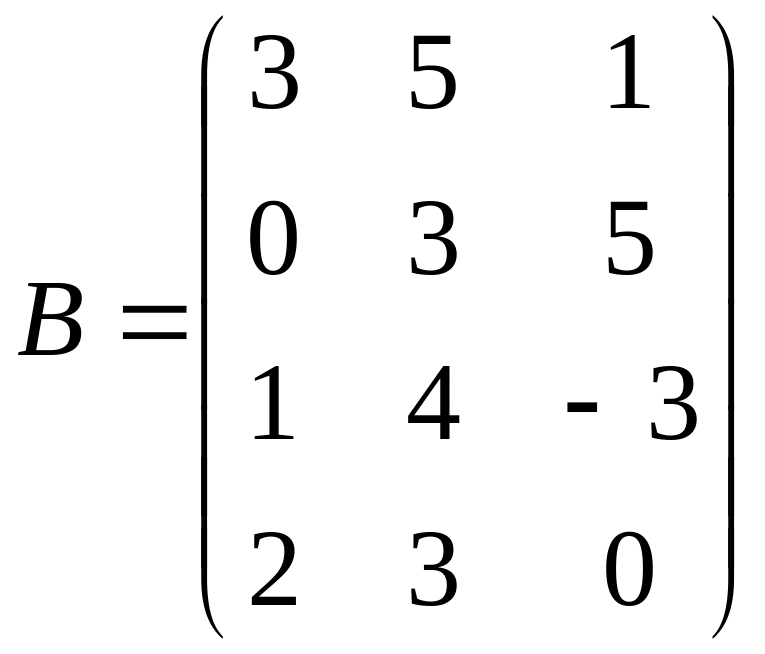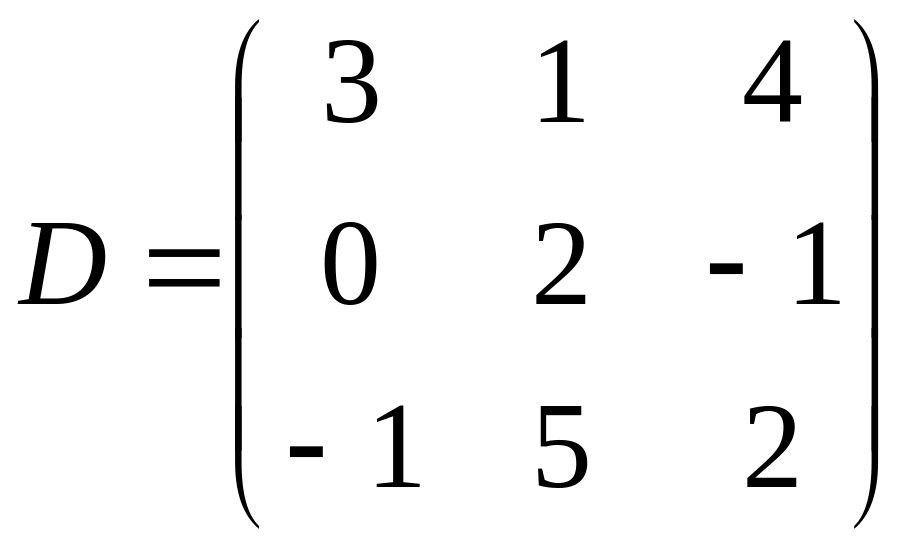4)
,
,
,
,
;
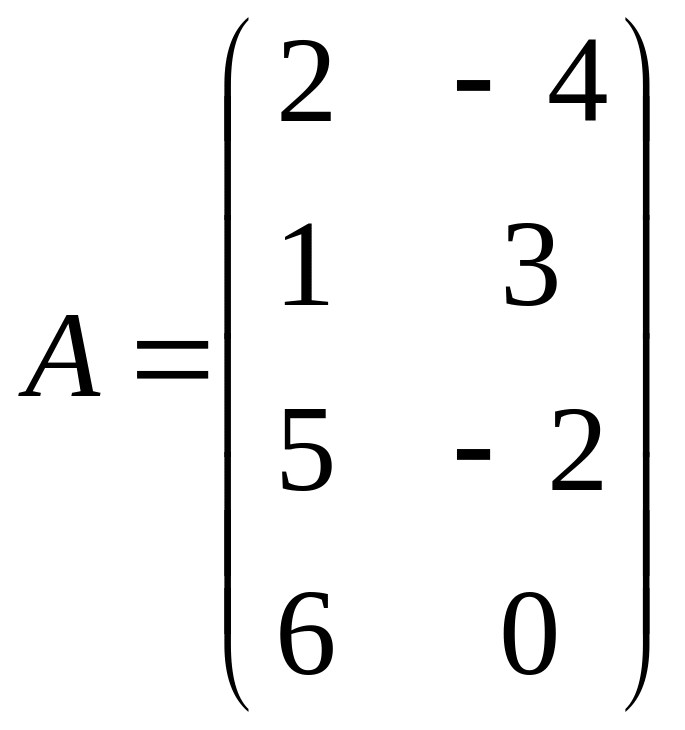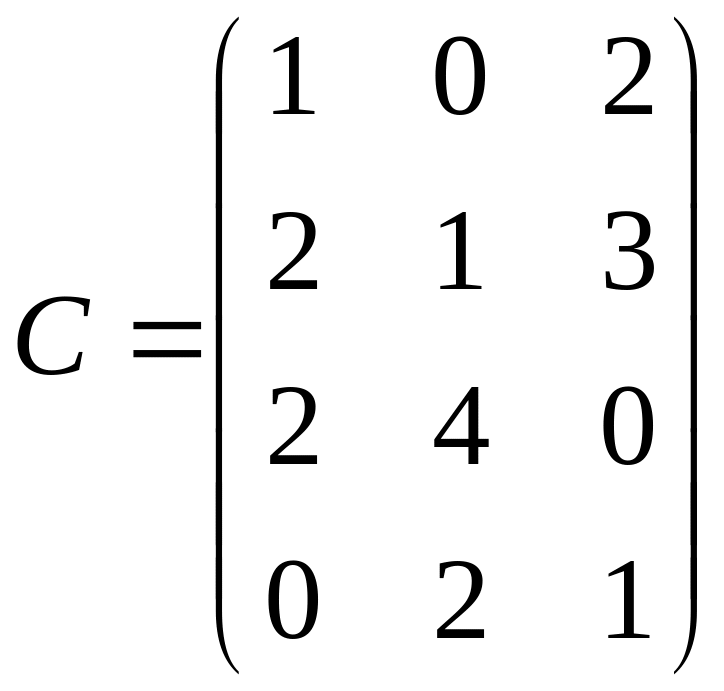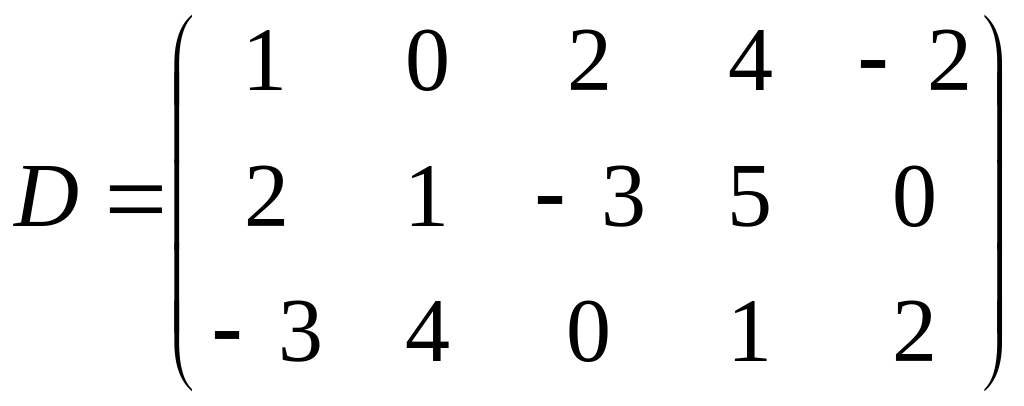5)
,
,
,
;
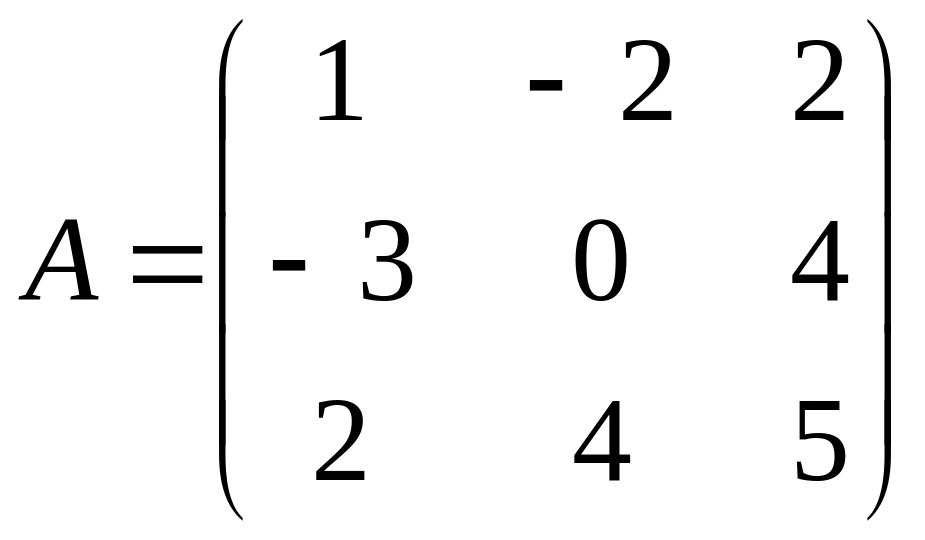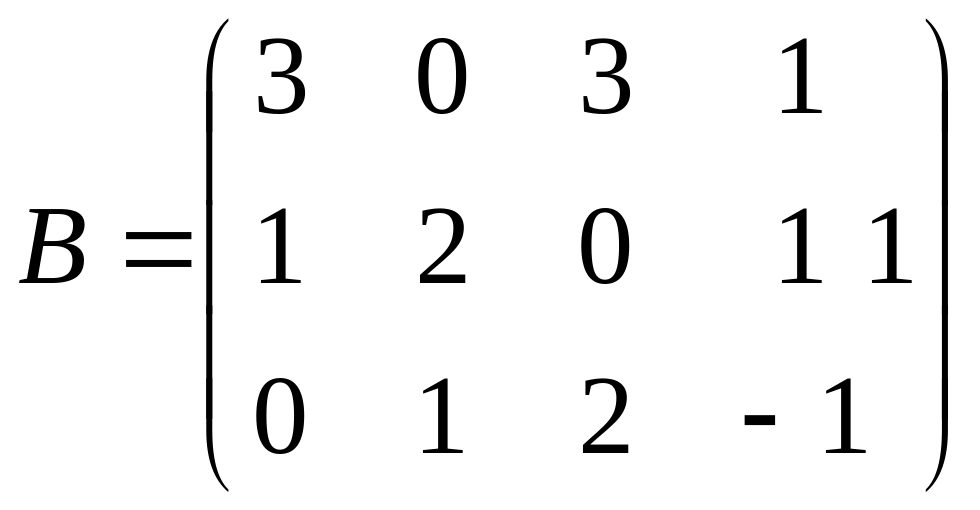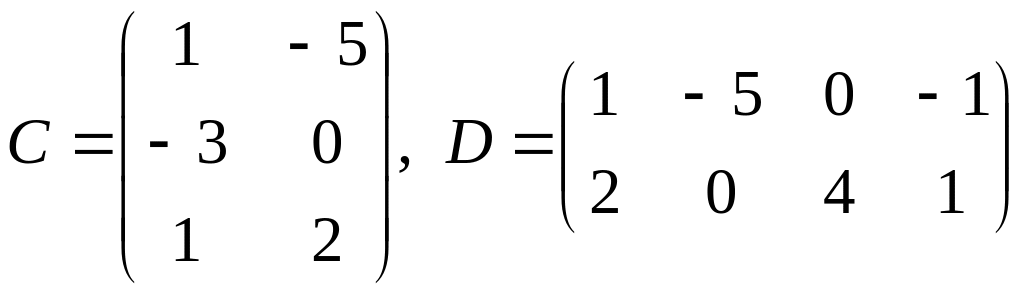6)
,
,
,
,
;
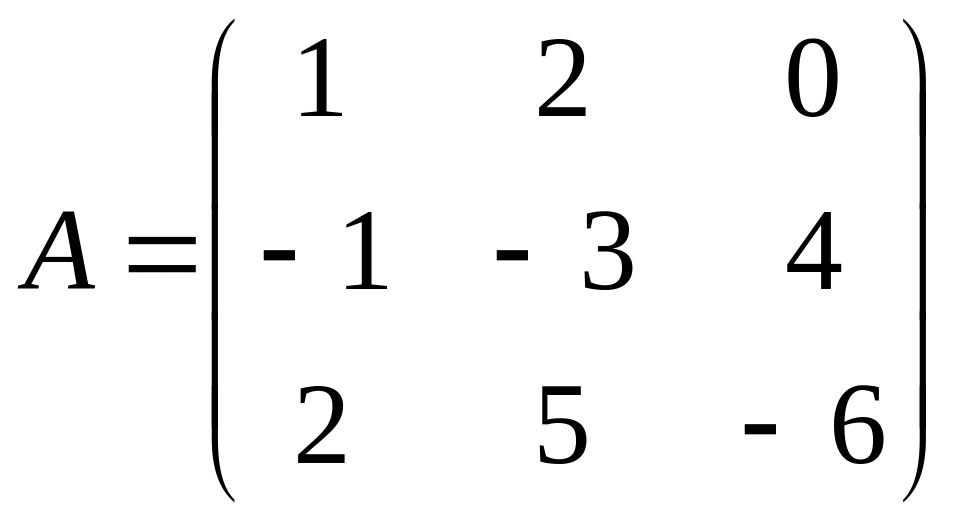7)
,
;
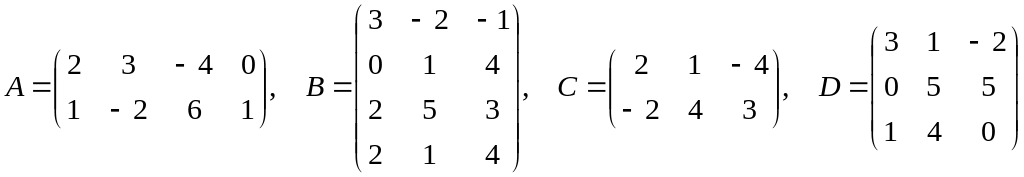8)
,
;
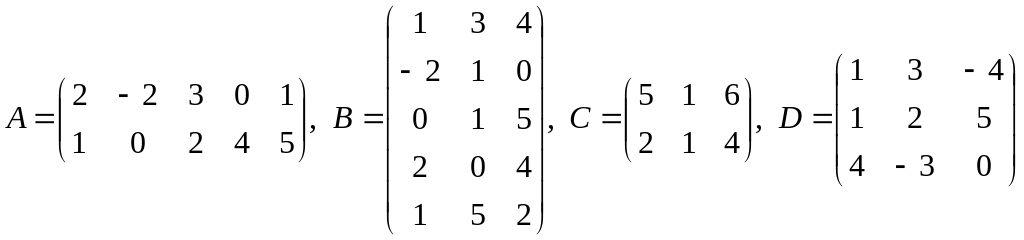9)
,
;
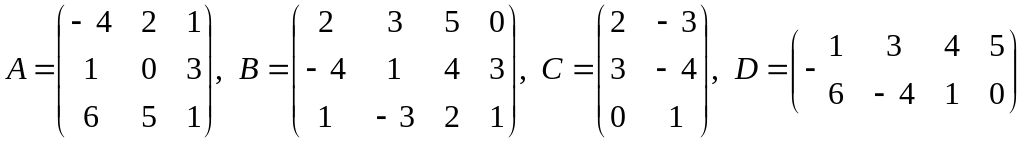10)
,
;
11)
,
;
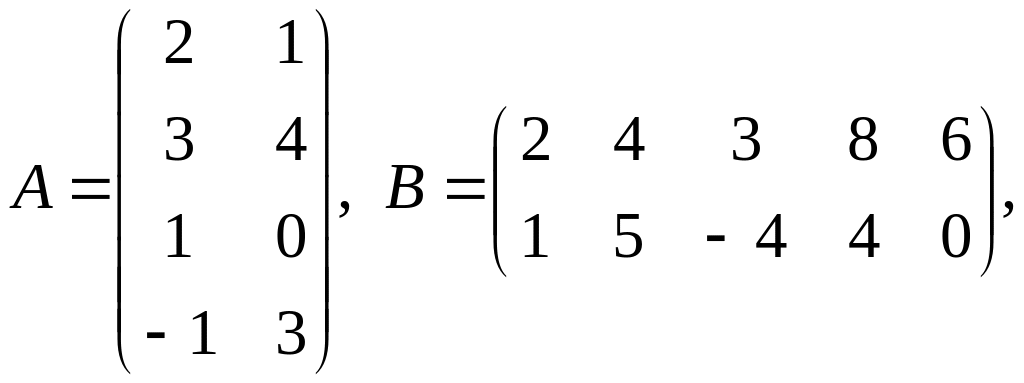
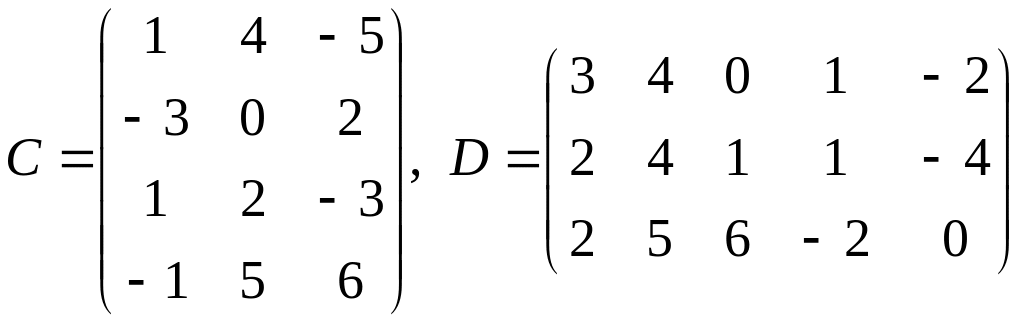12)
,
;
13)
,
;
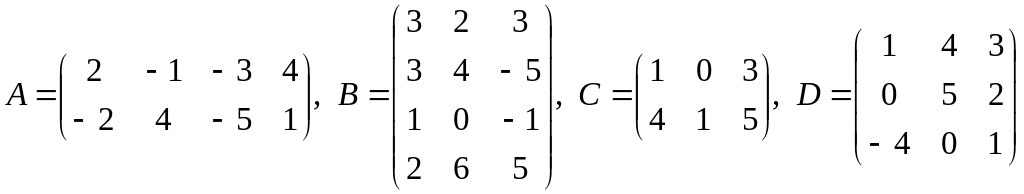14)
,
;
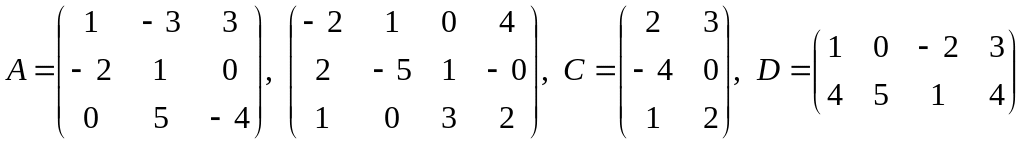15)
,
;
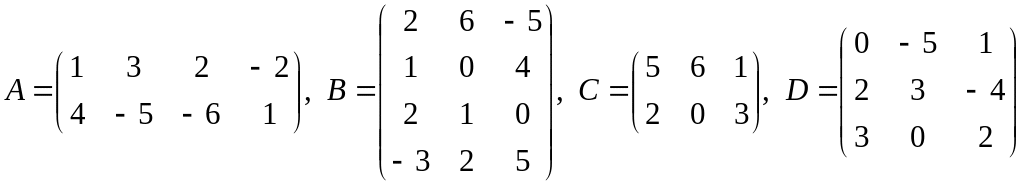16)
,
,
,
,
;
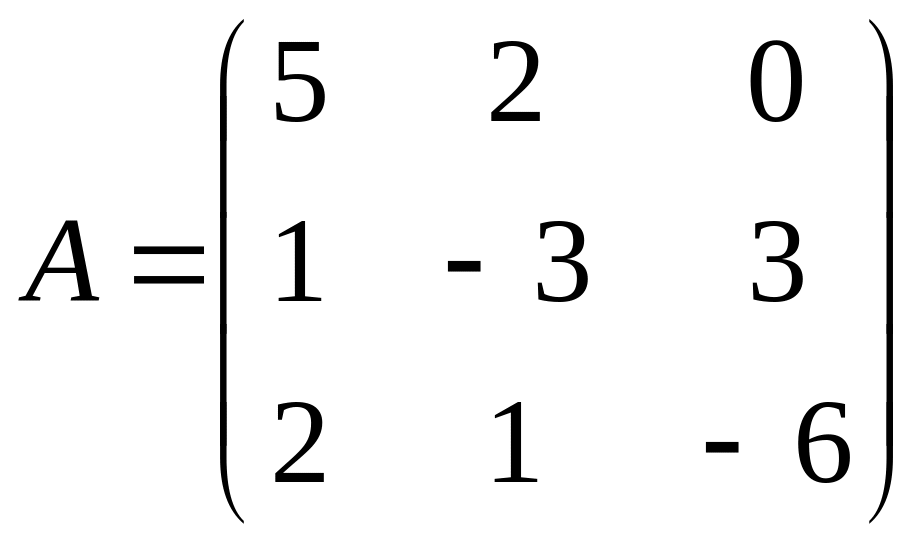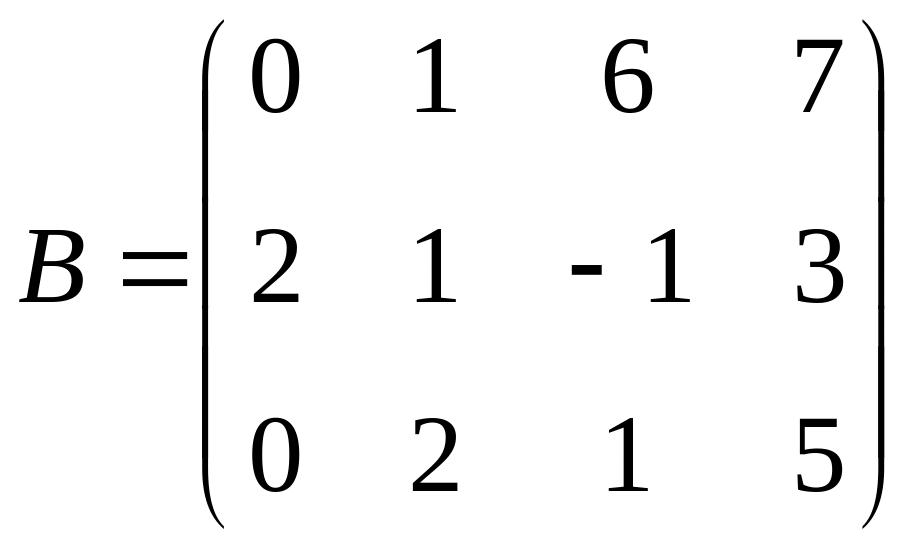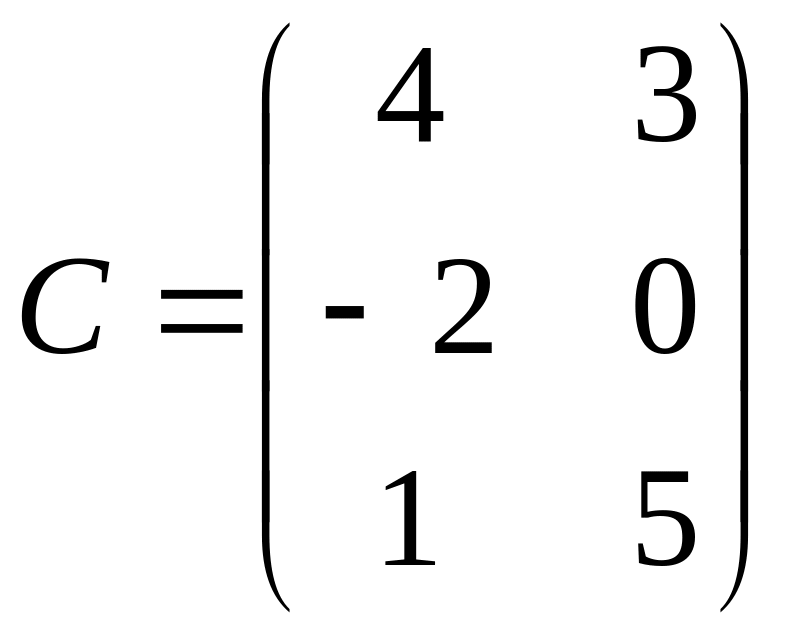17)
,
,
,
,
;
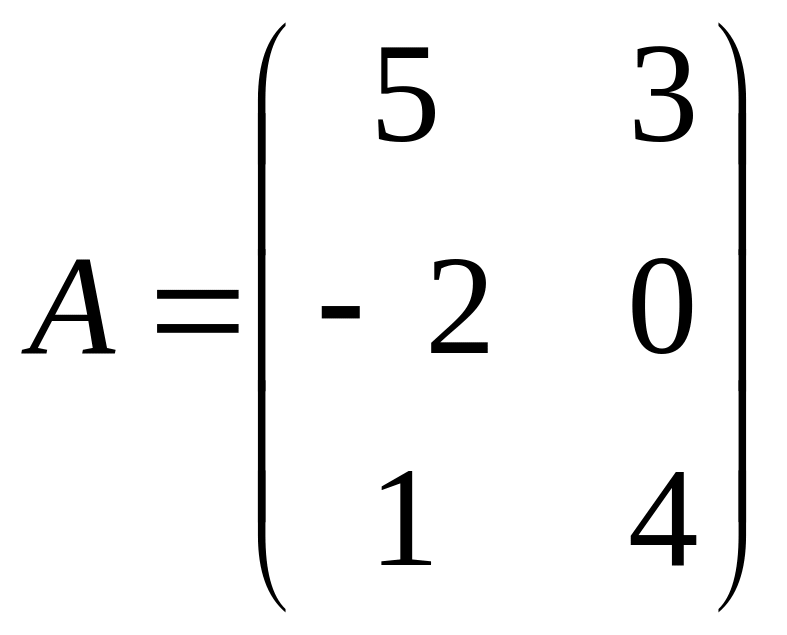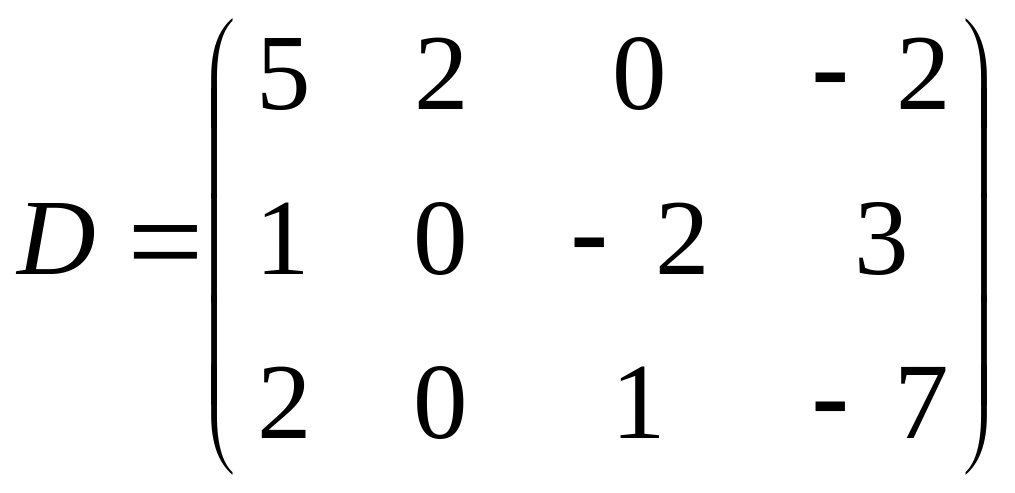18)
,
,
,
,
;
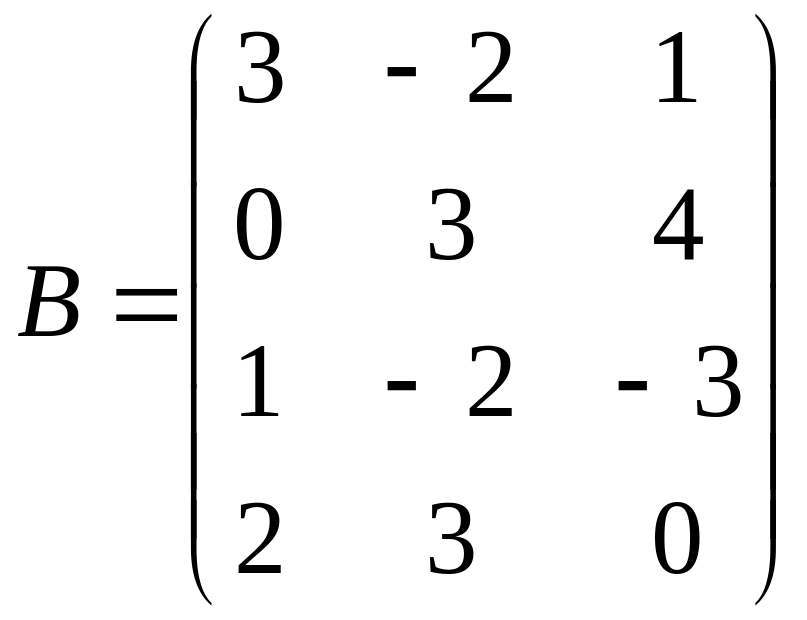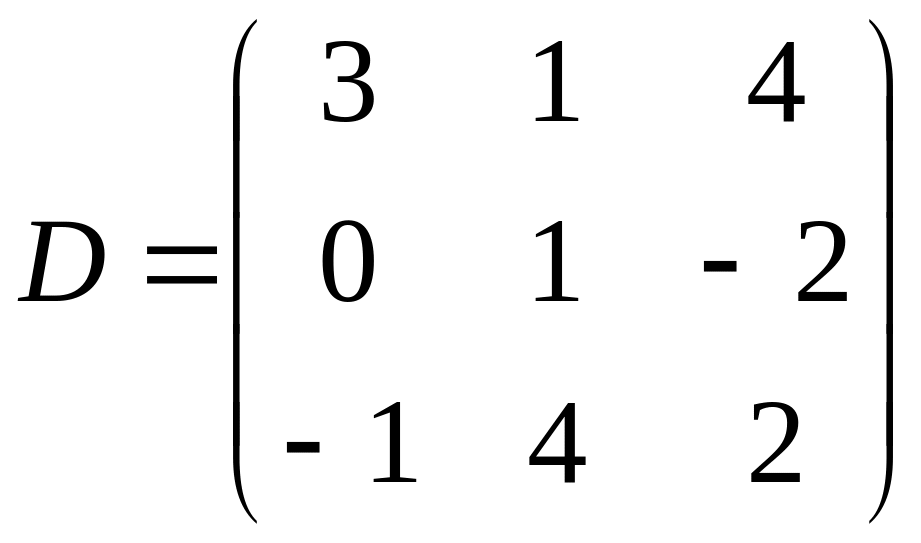19)
,
,
,
,
;
20) ,
,
,
;
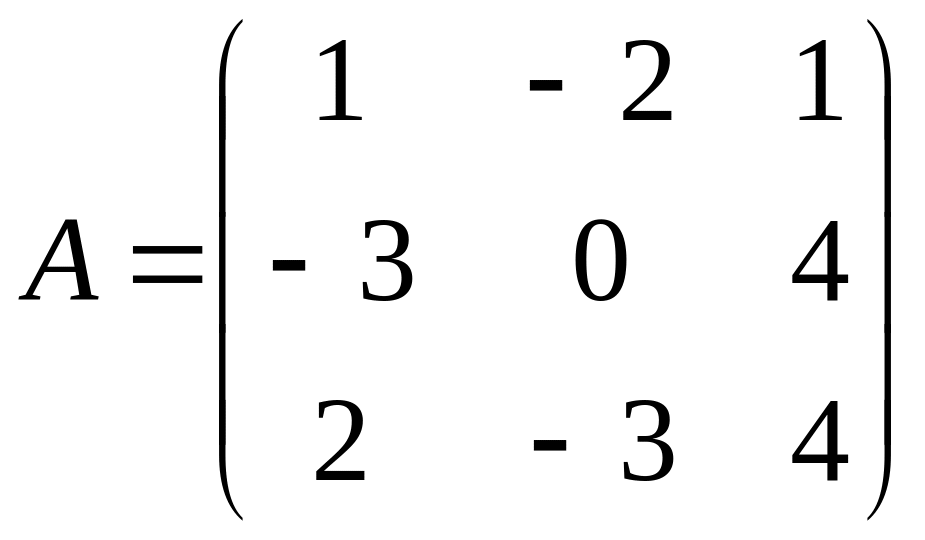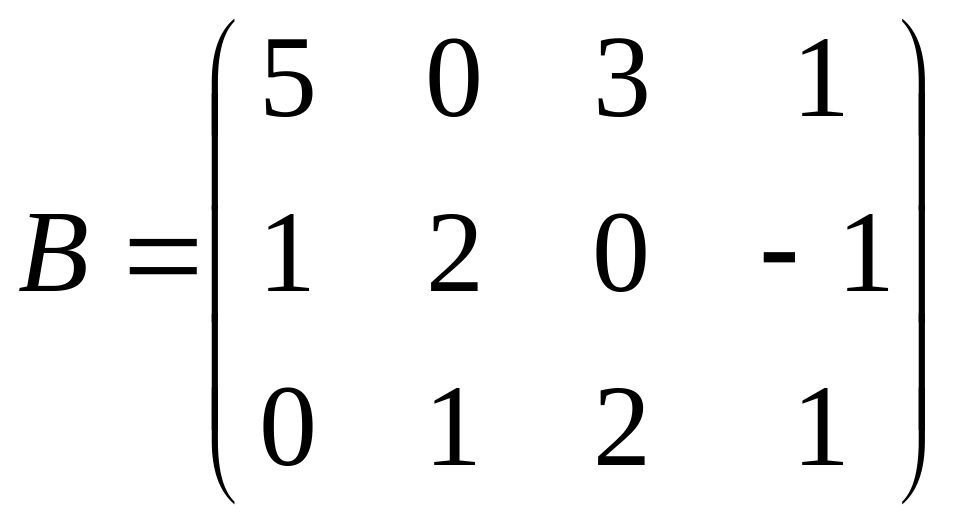21)
,
,
,
,
;
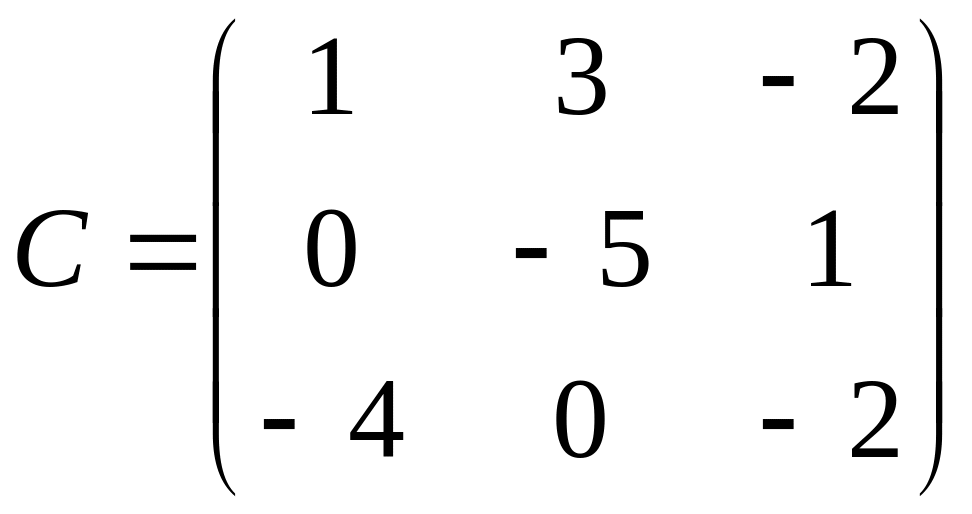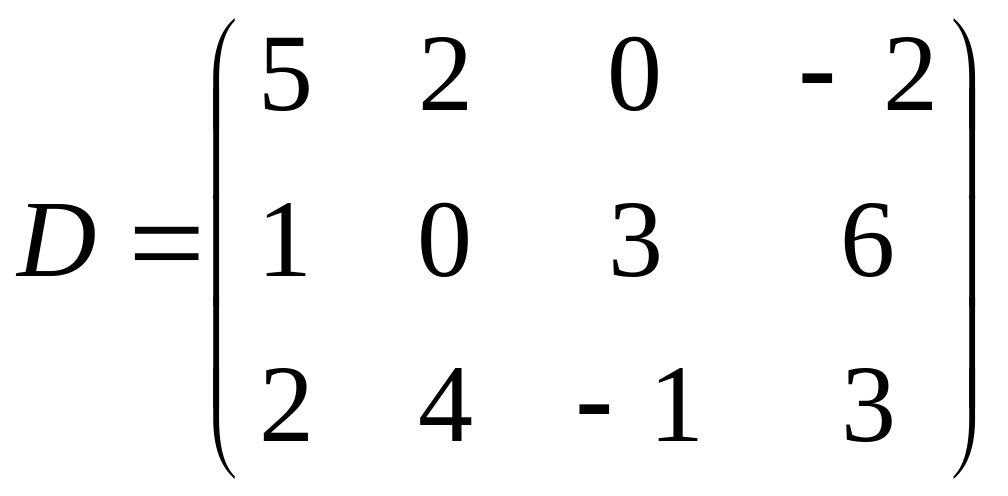22) ,
;
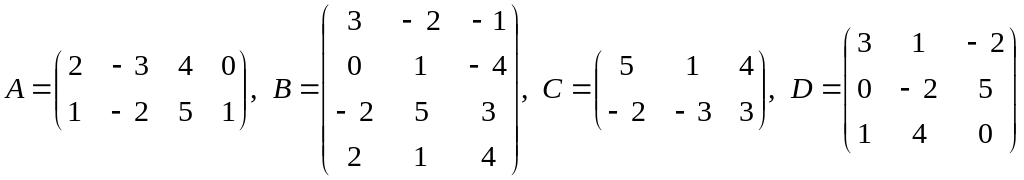23)
,
;
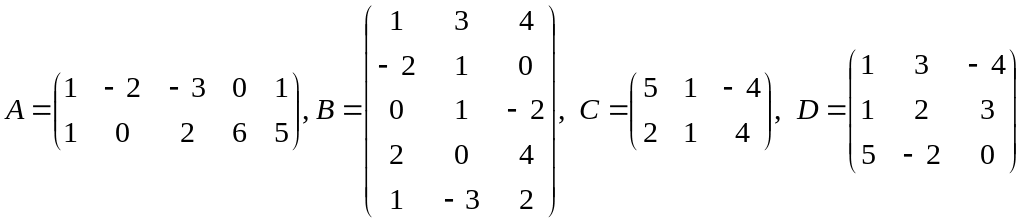24)
;
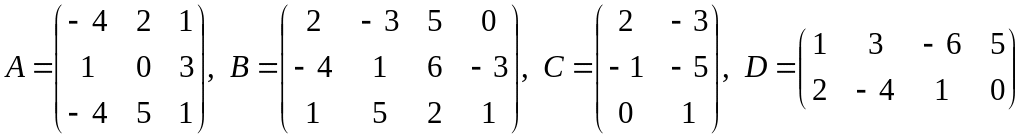25)
,
;
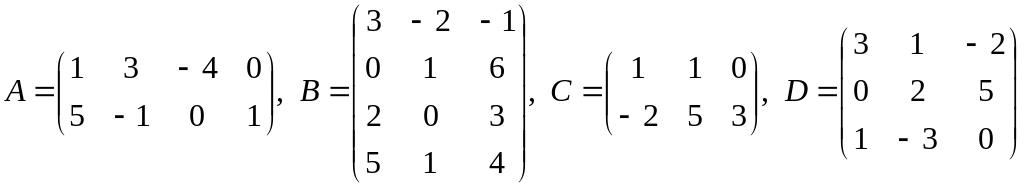26) ,
;
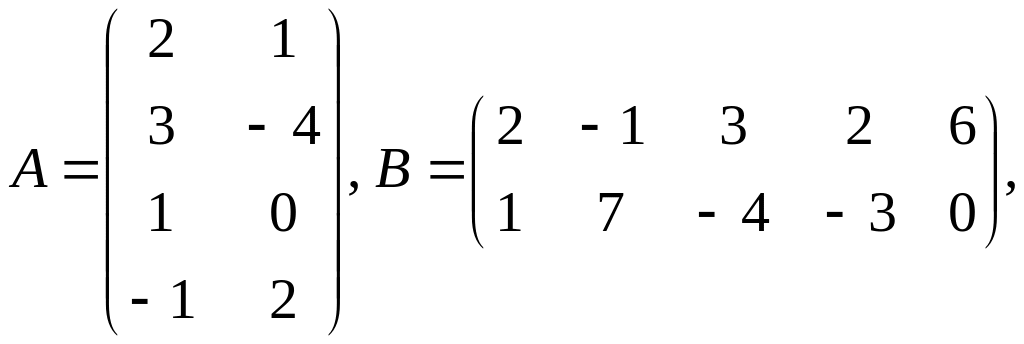
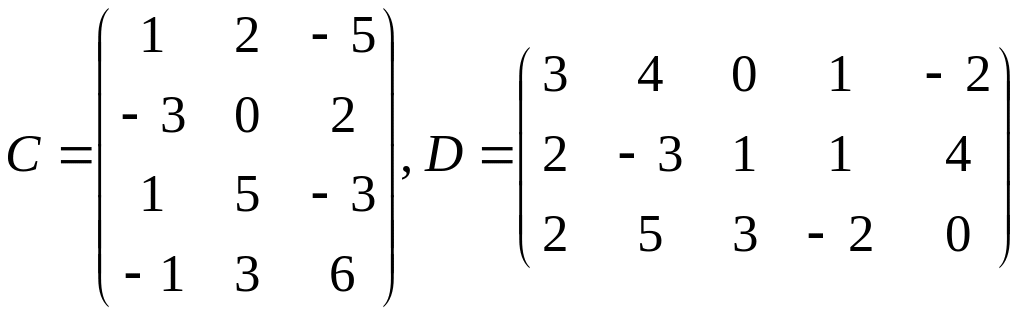27)
,
;
28)
,
;
29) ,
;
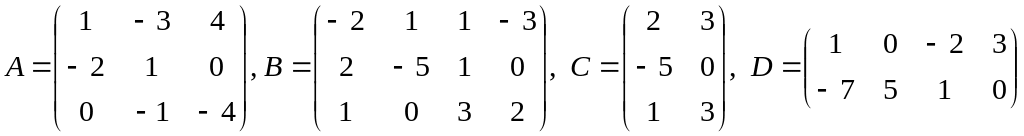30)
,
.
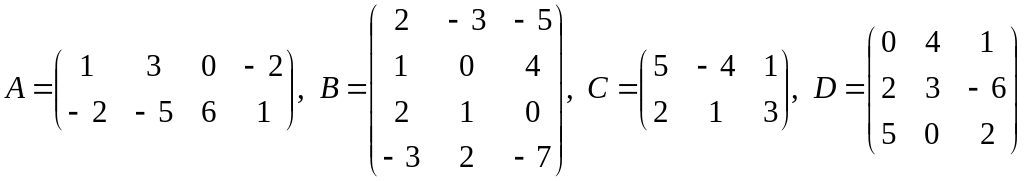III. Исследовать систему линейных уравнений на совместность и в случае совместности системы решить ее
а) матричным методом (методом обратной матрицы);
б) по формулам Крамера.
Сделать проверку.
Варианты:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
18)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29)
30)
