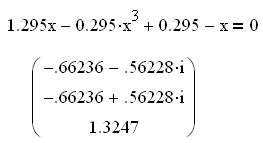4.Метод итераций( метод последовательных приближений)

Алгоритм метода:

1. Исходное уравнение f(x)=0 преобразуют к виду: x=(x)

2. Левая часть этого уравнения представляет уравнение прямой линии, проходящей через начало координат под углом в 45 к оси x. Абсцисса пересечения этой прямой с функцией  (x) и представляет корень уравнения f(x)=0

3. Задают начальное приближение x₀ и вычисляют значение функции  (x₀) Из следует, что его можно принять за первое приближение x₁ : x₁= (x₀).

4. Вычислив функцию  (x₁) , принимают это значение за второе приближение x₂= (x₁) и так далее. В общем случае для (i+1)-й итерации можно записать:

x_i+1= (x_i ).

5. Итерации повторяют, пока выполняется условие |x_i+1 – x_i | >  .

Геометрическая интерпретация метода показана на рис.4, причем на рис.4а) и 4б) процесс сходится к корню уравнения f(x)=0, а на рис.4в) и 4г) – расходится, хотя начальное приближение x₀ и выбрано для них ближе к корню.

Из рис.4а) можно заметить, что угол наклона касательной к любой точке кривой y= (x) не превышает 45 к оси x , т.е. ’(x)<1 . Из рис.4б) следует, что для этого случая ’(x)>-1.

На рис.4в) и 4г) это условие не соблюдается и итерационный процесс на них расходится от корня уравнения.

Отсюда следует, что для обеспечения сходимости итерационного процесса должно соблюдаться условие:

|’(x)|<1

Коррекция итерационного процесса

Вариант 1.

Приведение уравнения к инверсной форме {x= (x)}  {x= ^-1(x)}

Поясним на примере.

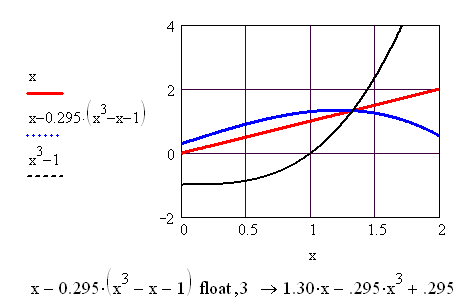
Найдём положительный корень уравнения x³ - x - 1= 0 (точное решение x=1,3247). Приведём уравнение к итерационной форме x=x³-1 и испробуем начальные приближения x₀ =1.3 и x₀ =1.4, очень близкие к искомому корню.

Процесс расходится, так как в окрестности корня производная (x³-1)^'=3x² > 1.

^{Воспользуемся инверсной формой x3=x + 1  .}

Процесс будет сходится, поскольку в окрестности корня

_{Это следует из известного правила:}

_{производная обратной функции g(x)=} ^-1_{(x) обратна производной функции (x) по величине.}

Можно проверить, что сходимость процесса будет при любом x₀ > 0

Вариант 2.

• Исходное уравнение f(x)=0 умножают на коэффициент : f(x)=0

• Прибавляют к обеим частям аргумент x: x=x+f(x)

• Для обеспечения сходимости процесса должно быть выполнено условие:

|[ x+f(x)]’|<1, или после преобразования|1+f’(x)|<1.

• Поскольку левая часть неравенства является модулем, то возможны два решения: 1-е решение: 1+f’(x)<1, или f’(x)<0;

2-е решение: -1-f’(x)<1, или f’(x)>-2.

Оба этих решения можно записать как: -2<f’(x)<0.

• Отсюда отыскивают границы диапазона значений C, при которых сходимость процесса будет обеспечена. В зависимости от знака f’(x) левую и правую границу диапазона коэффициента  вычисляют из следующих неравенств:

при f’(x)>0 при f’(x)<0

• Поскольку при поиске корня известны только абсциссы интервала [a_i ,b_i] , в котором находится корень, то необходимо вычислить границы диапазона  при значениях x_a и x_b и принять  как среднее арифметическое между ними.

Вариант 2.

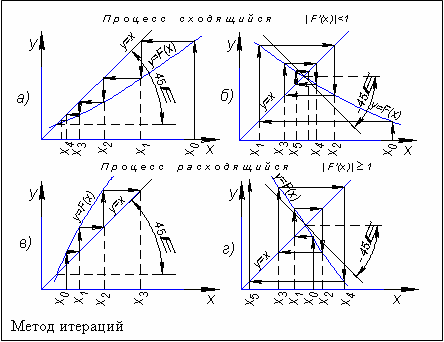
• Из рис.4а) и 4б) следует, что наибольшая скорость сходимости итерационного процесса будет при горизонтальном расположении кривой функции y=(x), т.е. когда ее первая производная будет равна нулю. Тогда можно записать равенство 1+f’(x)=0 , откуда

• В этом варианте также необходимо найти C для граничных точек интервала [a_i ,b_i], но уже по формуле

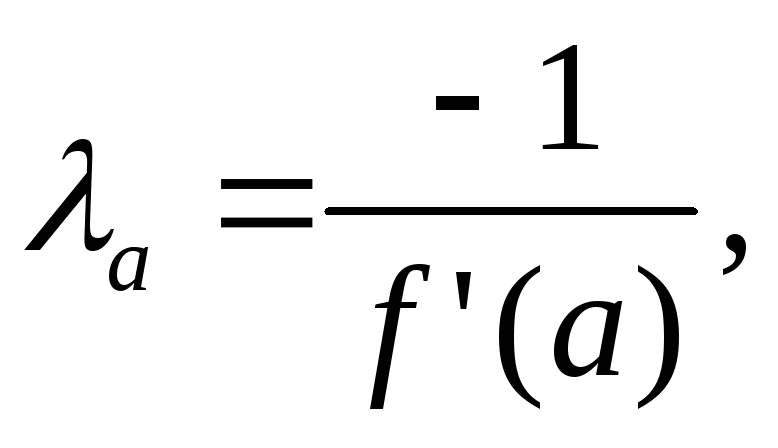
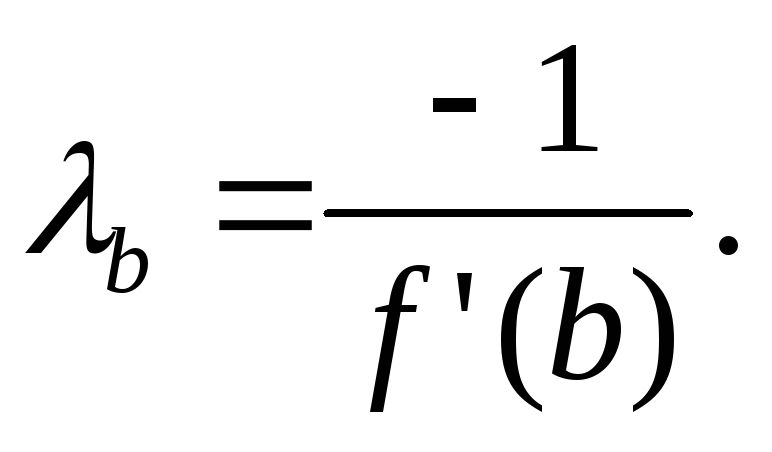
• Окончательное значение  для всего интервала можно принять как среднее арифметическое =(_a+_b) /2.

Для обоих вариантов начальное приближение можно принимать как

x₀=(x_a+x_b) /2.

Метод обладает теми же достоинствами и недостатками, что и предыдущий, к тому же добавляется необходимость вычислять коэффициент .

Пример:

В таком решении условия сходимости процесса итерации не выполняются

Воспользуемся множителем  :

Условие сходимости выполнено