Іі. Теоретичний огляд

ІІ.1. Чотириполюсники

ІІ.1.1. Визначення та класифікація

Чотириполюсник – це частина схеми електричного кола з двома парами виводів (полюсів), якими вона може з’єднуватись із рештою схеми.

Як правило, чотириполюсник виконує роль проміжної ланки між джерелом енергії та приймачем (споживачем). Прикладами ,,природних” чотириполюсників є двопровідна лінія електропередач, однофазний трансформатор, електричний фільтр, транзистор (біполярний, польовий) тощо.

Умовне позначення на схемах:

Рис. ІІ.1.1.

Полюси 1-1 чотириполюсника, до яких приєднується джерело живлення, називаються вхідними; полюси 2-2, до яких приєднується навантаження, – вихідними.

Режим чотириполюсника вважається повністю визначеним, якщо відомі вхідні та вихідні напруги і струми: .

Головна проблема теорії чотириполюсників – знайти дві електричні величини, які визначають режим чотириполюсника, якщо відомі дві інші. Основний зміст теорії чотириполюсників полягає в тому, що, користуючись деякими узагальненими параметрами чотириполюсника (первинними або

14

характеристичними), можна знаходити струми й напруги на його вході й виході.

За різними ознаками чотириполюсники можуть бути класифіковані наступним чином:

1. За ознакою лінійності елементів, які входять до нього, чотириполюсники поділяють на лінійні й нелінійні.

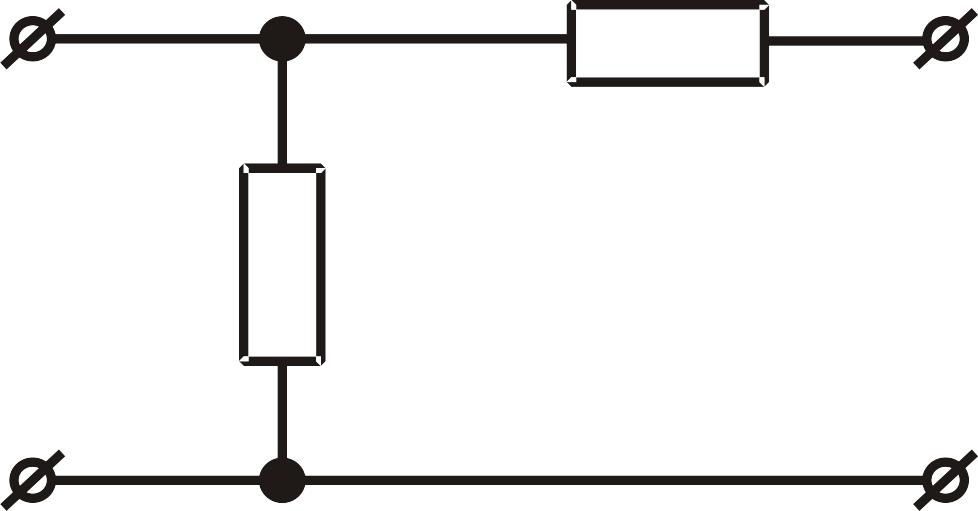
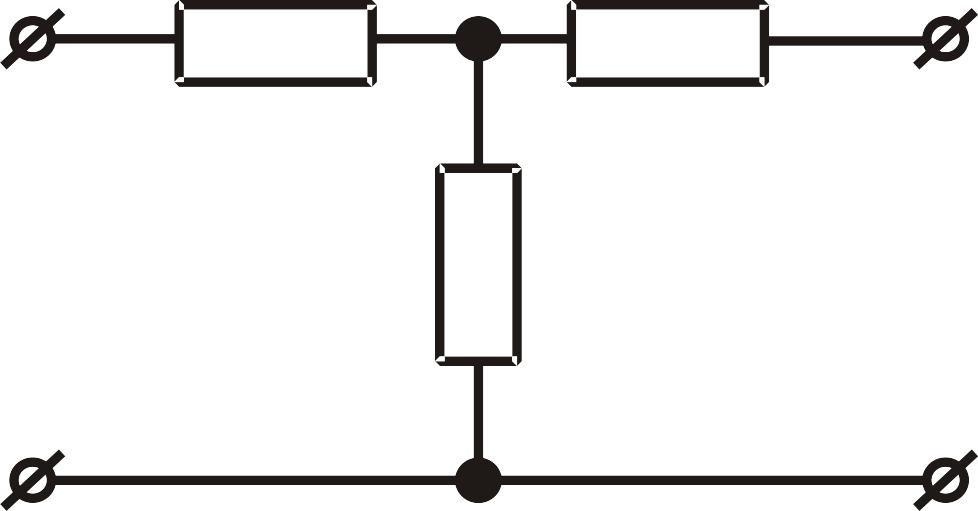
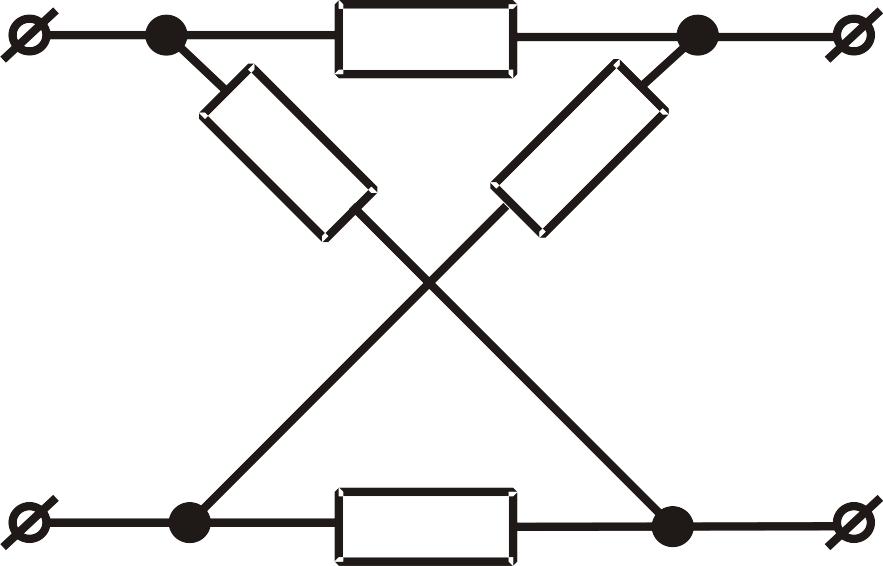
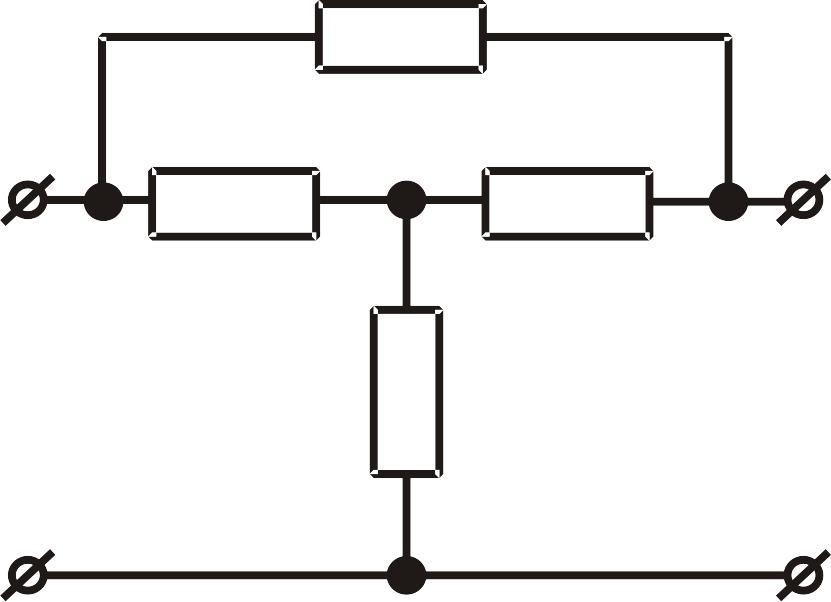
2. За схемою внутрішніх з’єднань елементів розрізняють Г-подібний, Т-подібний, П-подібний, М-подібний мостовий, Т-подібний мостовий тощо (рис. ІІ.1.2).

3. Чотириполюсники поділяють на активні й пасивні. Чотириполюсник називають активним, якщо він містить нескомпенсовані джерела електричної енергії. Якщо джерела електричної енергії в чотириполюснику відсутні, він називається пасивним.

4. Розрізняють симетричні й несиметричні чотириполюсники. Чотириполюсник симетричний, якщо зміна місцями його вхідних і вихідних виводів не змінює струми й напруги в решті кола.

5. Чотириполюсник називається зворотним, якщо виконується теорема зворотності, тобто відношення напруги на вході до струму на виході дорівнює відношенню вихідної напруги до вхідного струму ( 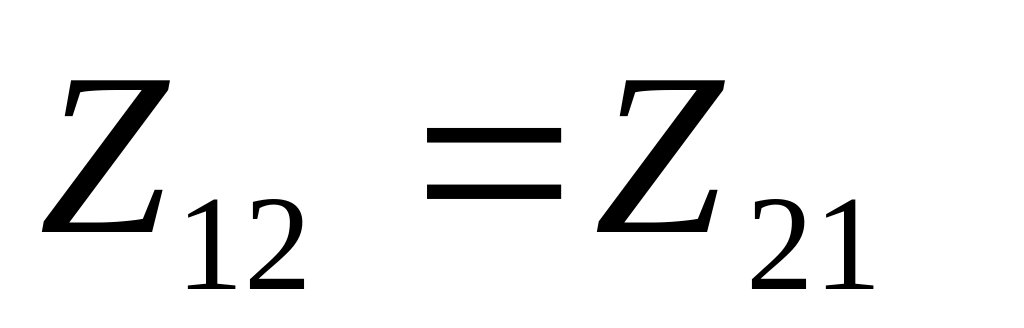або ).

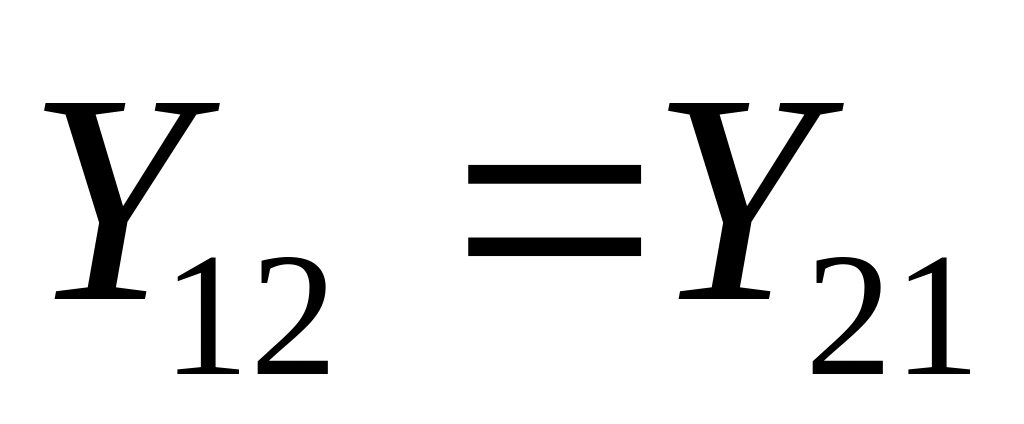Пасивні лінійні чотириполюсники й симетричні чотириполюсники (пасивні чи активні) завжди зворотні.

ІІ.1.2. Системи рівнянь чотириполюсника

Режим роботи чотириполюсника зі струмами (див. рис. ІІ.1.1) називають режимом прямого ввімкнення (енергія переноситься від входу чотириполюсника до виходу). Режим роботи чотириполюсника зі струмами називають режимом зворотного ввімкнення. Режим роботи чотириполюсника зі струмами називають режимом комбінованого ввімкнення.

15

а б

в г

д

Рис. ІІ.1.2. Типи чотириполюсників: а- Г-подібний; б - Т-подібний, в - П-подібний, г - М-подібний мостовий, д - Т-подібний мостовий.

Співвідношення між напругами та струмами на вході й виході чотириполюсника можуть бути записані у вигляді наступних шести форм рівнянь:

1. Форма струми визначаються в залежності від :

(ІІ.1.1)

16

1. Форма 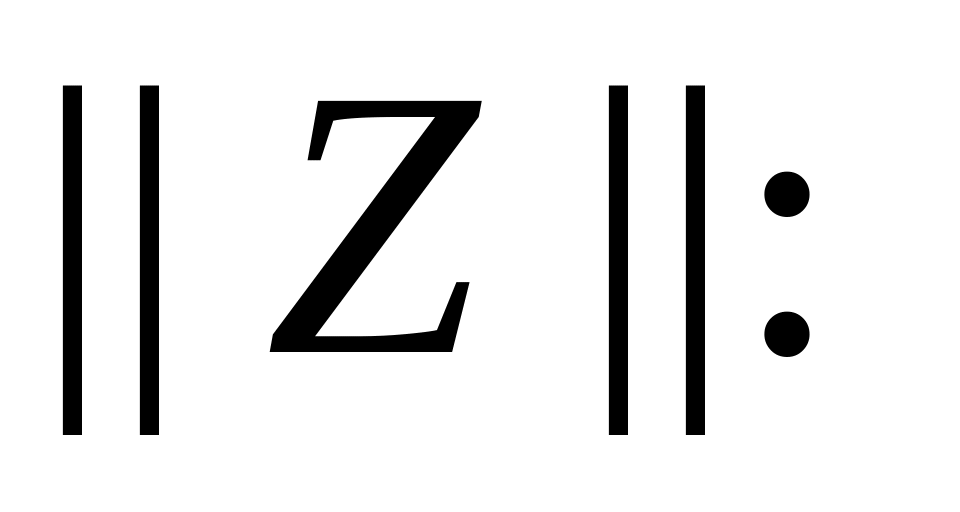напруги визначаються в залежності від :

(ІІ.1.2)

2. Форма вхідні напруга і струм визначаються в залежності від :

(ІІ.1.3)

3. Форма 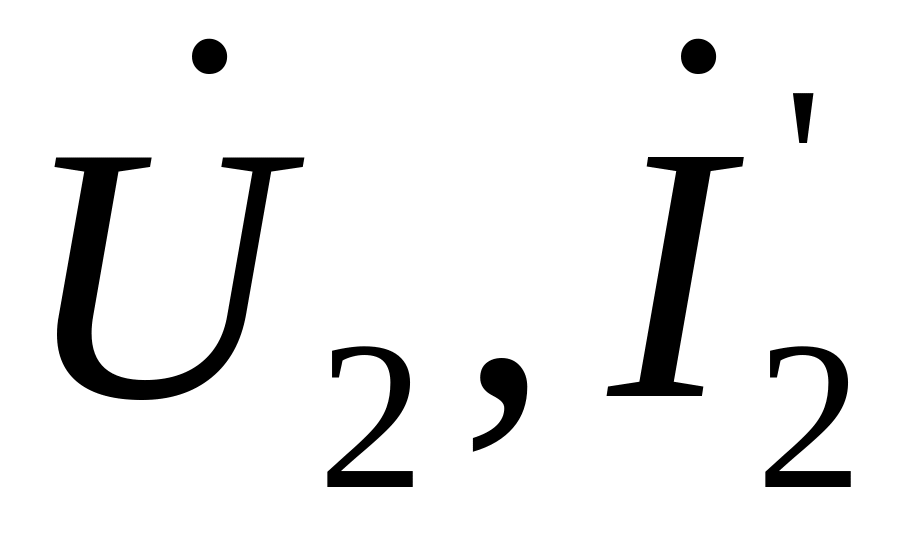визначаються в залежності від :

(ІІ.1.4)

4. Форма 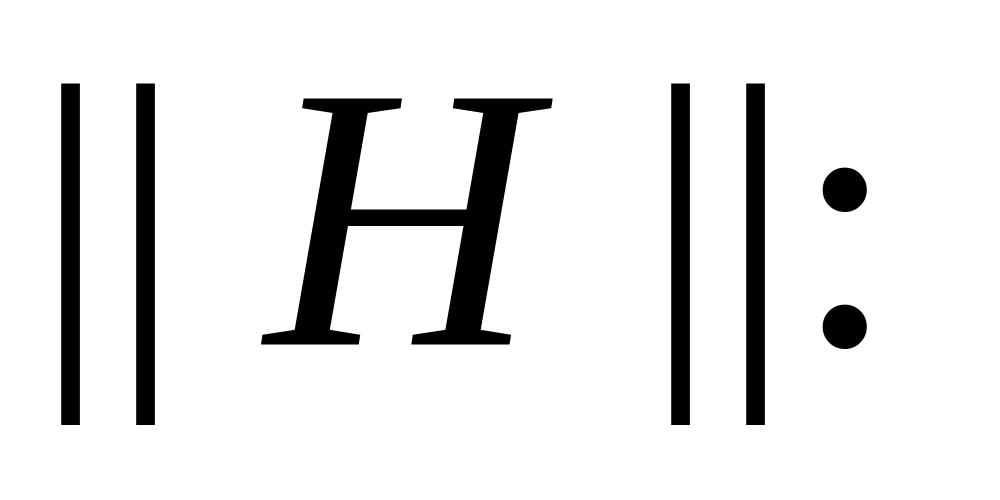параметри визначаються в залежності від :

(ІІ.1.5)

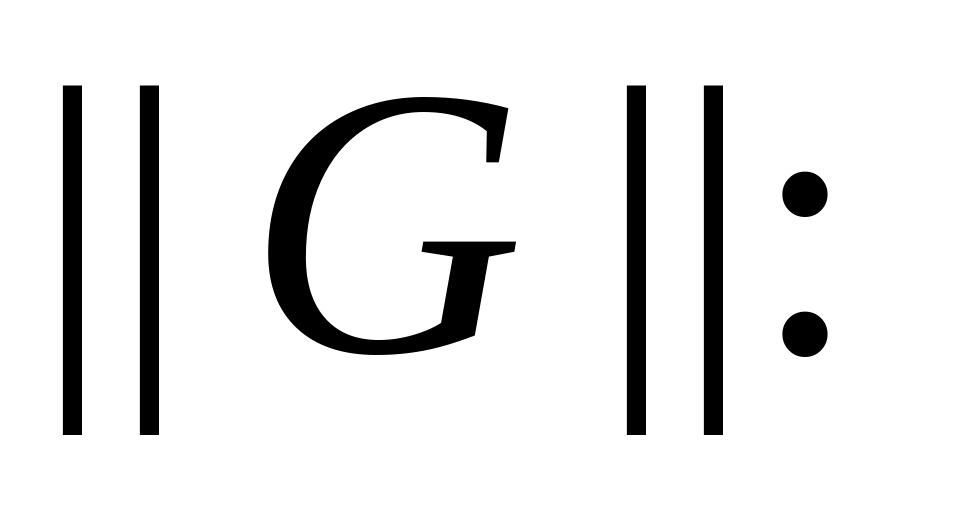
5. Форма 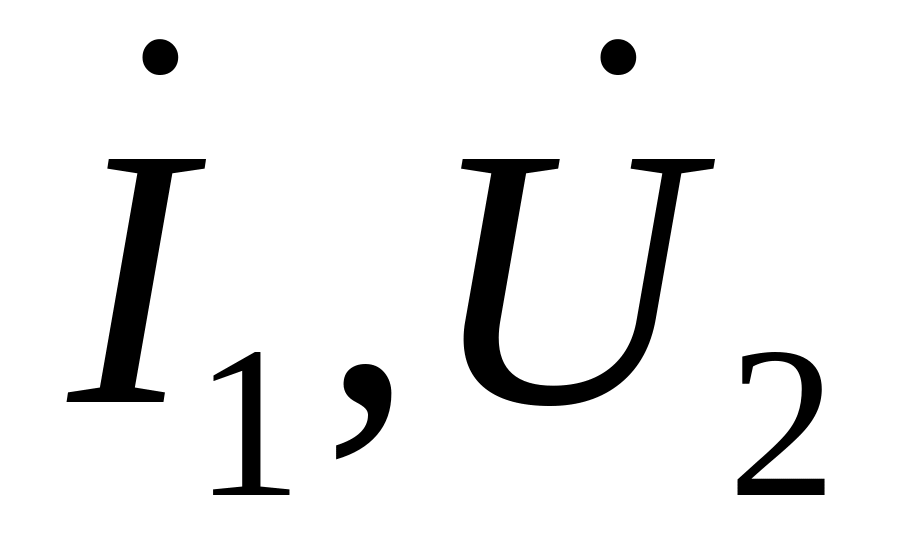визначаються в залежності від :

17

(ІІ.1.6)

Найбільш уживаними є перші чотири форми рівнянь. Коефіцієнти всіх форм рівнянь називають первинними параметрами чотириполюсника. Коефіцієнти різних форм взаємопов’язані між собою. Цей зв’язок наведено в Додатку 2.

Якщо чотириполюсник зворотний, то виконується умова

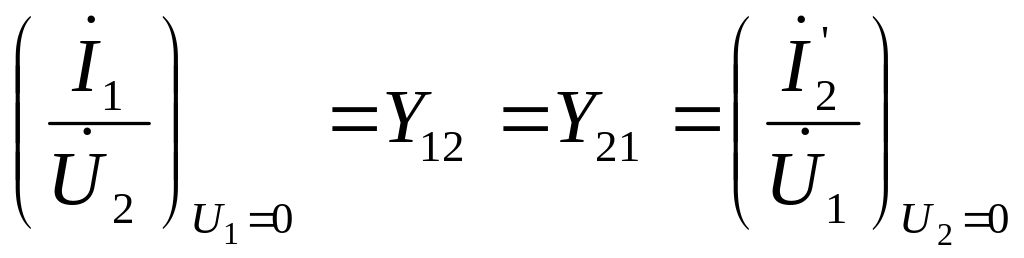. (ІІ.1.7)

Якщо чотириполюсник симетричний, то виконується умова

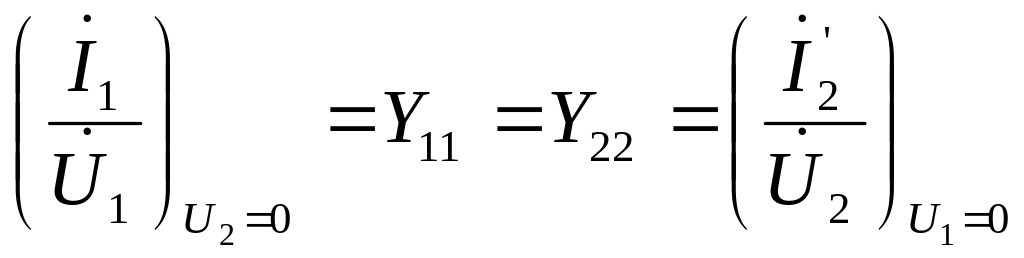. (ІІ.1.8)

Враховуючи зв’язок коефіцієнтів різних форм рівнянь чотириполюсника, форму рівнянь можна виразити через коефіцієнти форми в наступному вигляді:

(ІІ.1.9)

ІІ.1.3 Визначення первинних параметрів пасивного чотириполюсника

Універсальним є метод холостого ходу й короткого замикання, суть якого полягає у визначенні наступних чотирьох параметрів:

18

вхідного опору з боку полюсів 1-1 при розімкнених 2-2

; (ІІ.1.10)

вхідного опору з боку полюсів 1-1 при замкнених 2-2

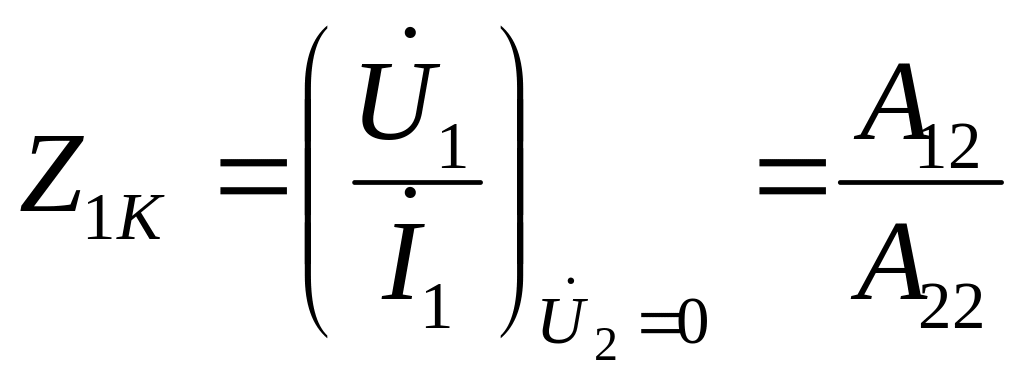; (ІІ.1.11)

вхідного опору з боку полюсів 2-2 при розімкнених 1-1

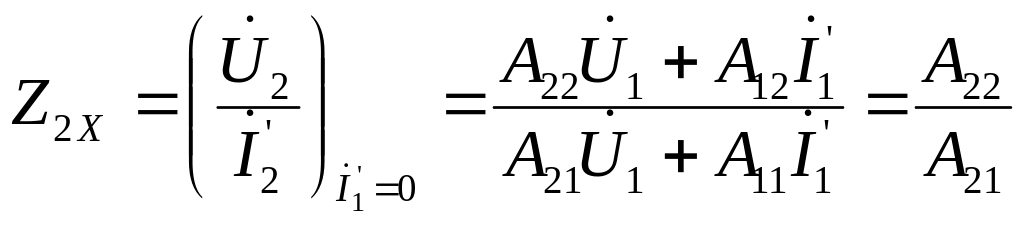; (ІІ.1.12)

та вхідного опору з боку полюсів 2-2 при закорочених 1-1

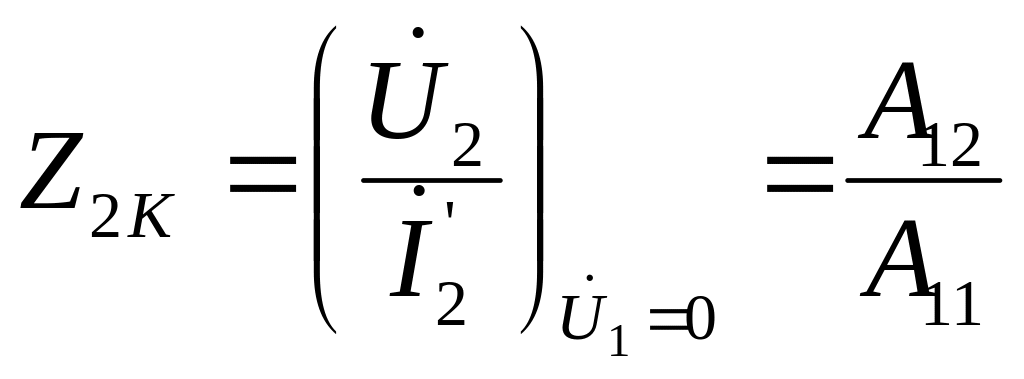. (ІІ.1.13)

Ці параметри можуть бути розраховані аналітично або визначені емпірично.

Розв’язавши систему рівнянь (ІІ.1.10)-( ІІ.1.13) відносно первинних параметрів чотириполюсника, одержимо:

; (ІІ.1.14)

; (ІІ.1.15)

19

; (ІІ.1.16)

. (ІІ.1.17)

Правильність розрахунку параметрів -форми рівнянь перевіряємо співвідношенням

, (ІІ.1.18)

де – визначник матриці коефіцієнтів .

За допомогою таблиці (Додаток 2) можна знайти коефіцієнти інших форм рівнянь чотириполюсника. Для коефіцієнтів -форми, наприклад, одержимо:

. (ІІ.1.19)

Складний чотириполюсник можна розглядати як сукупність відповідним чином з’єднаних простих чотириполюсників (Г-подібних, Т-подібних, П-подібних тощо).

Теорія чотириполюсників дозволяє знайти параметри такого складного чотириполюсника за параметрами його складових простих чотириполюсників.

Для одержання параметрів складного чотириполюсника зручно користуватись записом параметрів у матричній формі.

Розрізняють наступні п’ять методів з’єднання простих чотириполюсників у складному: каскадне, послідовне, паралельне, послідовно-паралельне, паралельно-послідовне. У залежності від схеми з’єднання простих чотириполюсників у складному, для аналізу застосовується відповідна форма рівнянь.

20

Каскадне з’єднання (рис. ІІ.1.3) – це з’єднання, при якому вхідні виводи наступного чотириполюсника під’єднуються до вихідних виводів попереднього. Тобто це з’єднання має наступний вигляд:

Рис. ІІ.1.3.

При каскадному з’єднанні для аналізу застосовується -форма рівнянь чотириполюсника, причому

, (ІІ.1.20)

де – матриця коефіцієнтів -форми рівнянь складного чотириполюсника;

– такі ж матриці для простих чотириполюсників.

Послідовне з’єднання (рис. ІІ.1.4):

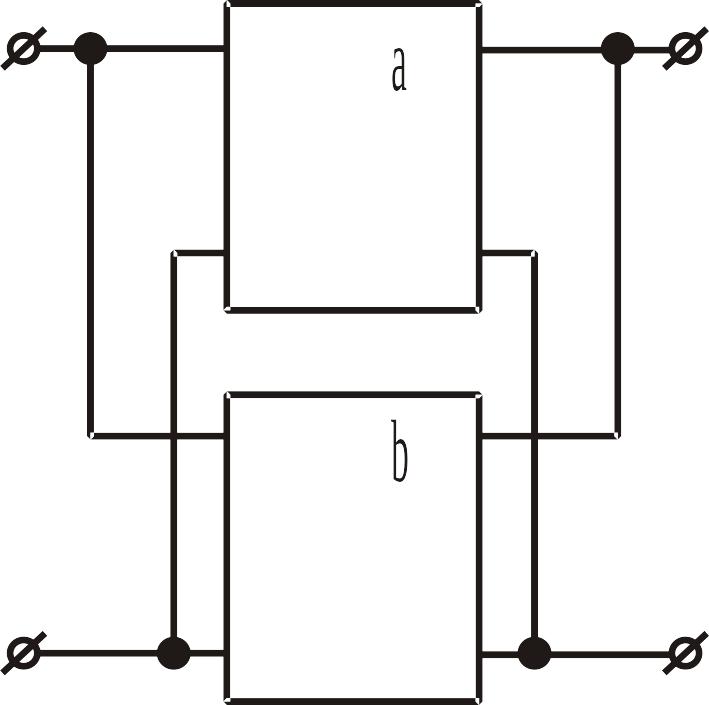
Рис. ІІ.1.4. Рис. ІІ.1.5.

21

Для аналізу застосовується -форма рівнянь, причому

. (ІІ.1.21)

Паралельне з’єднання (рис. ІІ.1.5)

Для аналізу застосовується -форма рівнянь, причому

. (ІІ.1.22)

Послідовно-паралельне з’єднання (рис. ІІ.1.6):

Рис. ІІ.1.6. Рис. ІІ.1.7.

Для аналізу застосовується -форма рівнянь, причому

. (ІІ.1.23)

Паралельно-послідовне з’єднання (рис. ІІ.1.7)

Для аналізу застосовується -форма рівнянь, причому

. (ІІ.1.24)

22

Розглянемо зв’язок (без виводу) між первинними параметрами чотириполюсника та параметрами (опорами) Г-, Т-, П-подібних схем простих чотириполюсників.

Для Г-схеми (рис. ІІ.1.8):

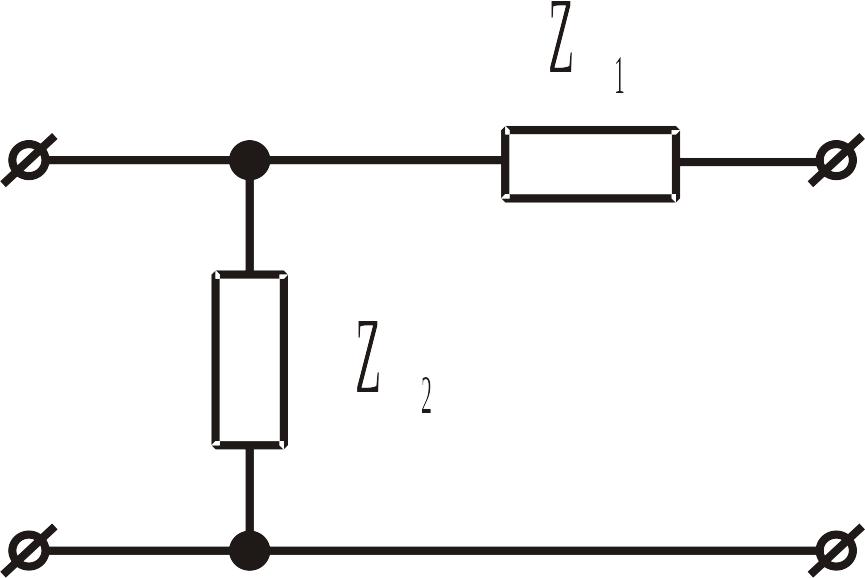
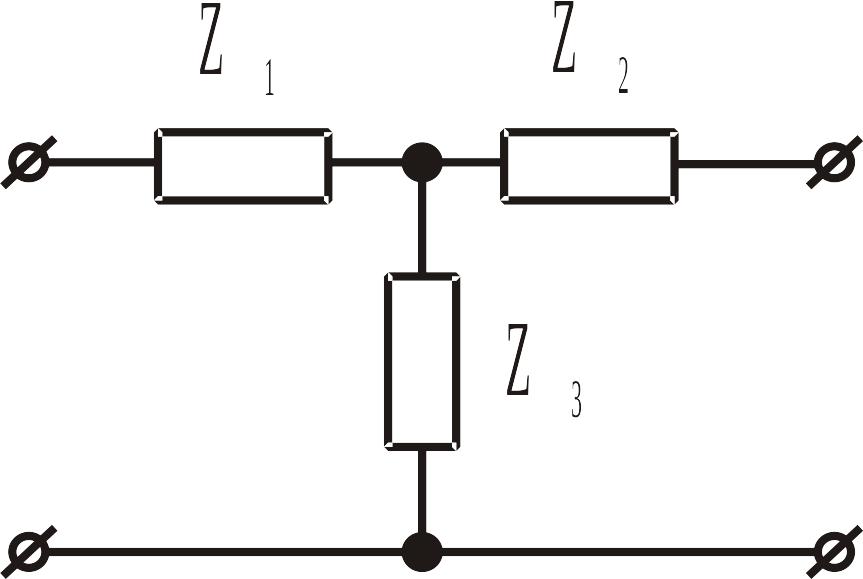
Рис. ІІ.1.8. Рис. ІІ.1.9.

(ІІ.1.25)

Для Т-схеми (рис. ІІ.1.9):

(ІІ.1.26)

Для П-схеми (рис. ІІ.1.10):

Рис. ІІ.1.10.

23

(ІІ.1.27)

ІІ.1.4. Характеристичні параметри пасивного чотириполюсника

До характеристичних параметрів пасивного чотириполюсника належать характеристичні опори , коефіцієнт передачі g та коефіцієнт трансформації m_Т.

Характеристичний опір – це вхідний опір чотириполюсника у випадку, коли вихід чотириполюсника навантажений опором .

Характеристичний опір – це вхідний опір чотириполюсника з боку вихідних виводів у випадку, коли до вхідних виводів під’єднано навантаження . З первинними параметрами характеристичні опори пов’язані співвідношеннями

; (ІІ.1.28)

. (ІІ.1.29)

Відношення

(ІІ.1.30)

називають коефіцієнтом трансформації чотириполюсника.

24

Ввівши поняття коефіцієнта трансформації m_Т, рівняння чотириполюсника в -формі (з урахуванням того, що ) можна записати у вигляді

; (ІІ.1.31)

. (ІІ.1.32)

Комплексну величину

(ІІ.1.33)

називають коефіцієнтом передачі пасивного чотириполюсника (сталою передачі).

Коефіцієнт передачі g є, в загальному випадку, комплексною величиною, тобто

, (ІІ.1.34)

де – коефіцієнт згасання,

– коефіцієнт фази.

Якщо чотириполюсник симетричний , коефіцієнт передачі g можна визначити за формулою

. (ІІ.1.35)

25

Представивши комплексні напруги і в показниковій формі, одержимо:

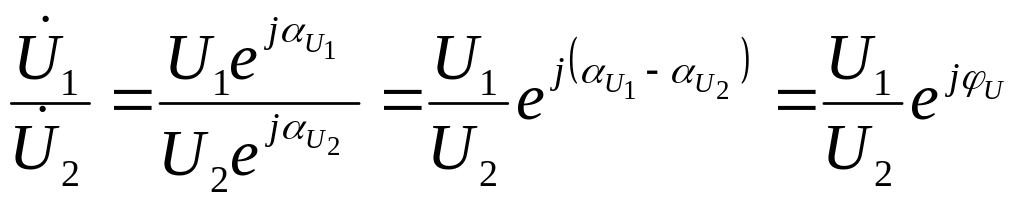. (ІІ.1.36)

Тоді

. (ІІ.1.37)

Порівнюючи (ІІ.1.34) і (ІІ.1.37), одержимо

; ; (ІІ.1.38)

або

; . (ІІ.1.39)

З (ІІ.1.38) випливає, що

. (ІІ.1.40)

Тобто коефіцієнт а дійсно характеризує згасання напруги (або струму) в чотириполюснику. Коефіцієнт а вимірюється в неперах. Згасанню в 1 нп відповідає відношення

. (ІІ.1.41)

26

ІІ.2. Реактивні електричні фільтри

ІІ.2.1. Визначення. Умови пропускання

Електричний фільтр являє собою пасивний чотириполюсник, який пропускає певну смугу частот із малим затуханням. Цю смугу частот називають смугою прозорості фільтра. Решта частот складає смугу затримки або згасання.

Реактивні фільтри – це фільтри, які складаються з елементів L і C.

Найменша кількість елементів, з яких може складатися фільтр, дорівнює двом (Г-подібна ланка). Фільтри, що містять Т- і П-подібні ланки (рис. ІІ.2.1), можуть бути утворені каскадним з’єднанням Г-подібних ланок.

а б

Рис. ІІ.2.1. Симетричні Т (а)- і П (б)-подібні фільтри.

У випадку симетричного Т- або П-подібного фільтра постійна передачі g визначається за формулою

. (ІІ.2.1)

Смуга пропускання (прозорості) реактивного фільтра – це смуга частот, при яких власне згасання фільтра дорівнює нулю .

Для довільного симетричного реактивного фільтра в смузі

27

пропускання, тобто при , виконується умова

. (ІІ.2.2)

Оскільки значення функції косинус змінюються в межах від -1 до 1, то для симетричного Т- або П-подібного фільтра одержимо

(ІІ.2.3)

або

. (ІІ.2.4)

Нерівність (ІІ.2.4) називають умовою пропускання реактивного фільтра.

Випадок рівності у виразі (4) відповідає умові визначення граничних частот (частот зрізу) смуги пропускання, тобто

. (ІІ.2.5)

Варто зазначити, що пасивний чотириполюсник має фільтруючу властивість (характеризується смугою прозорості) тільки в тому випадку, коли опори і різнохарактерні. Тобто, якщо – індуктивний опір, то повинен бути ємнісним і навпаки.

ІІ.2.2. Частотні характеристики фільтра

Частотними характеристиками фільтра називають залежності характеристичних параметрів від частоти, тобто залежності або .

28

У зоні прозорості фільтра

. (ІІ.2.6)

У зоні згасання (затримки)

. (ІІ.2.7)

Коефіцієнт фази , якщо , якщо .

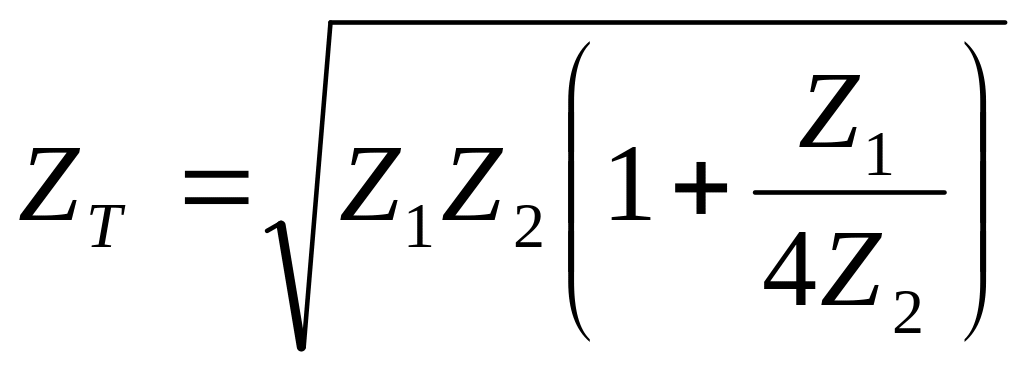; (ІІ.2.8)

. (ІІ.2.9)

ІІ.2.3. Фільтри типу k

Якщо складові елементи Г-подібної ланки фільтра – взаємно обернені двополюсники (елементи L і C), то добуток їх комплексних опорів у всьому діапазоні частот є постійним і не залежить від частоти:

, (ІІ.2.10)

де – дійсне число.

29

Фільтри, які відповідають умові (ІІ.2.10), одержали назву фільтрів типу k. Розрізняють фільтри нижніх частот, фільтри верхніх частот, смугові й загороджувальні фільтри типу k.

ІІ.2.3.1 Реактивні низькочастотні фільтри типу k

Низькочастотним називають фільтр, який пропускає без згасання струми з частотами від до ( – частота зрізу). Схеми НЧ фільтрів зображені на рис. ІІ.2.2.

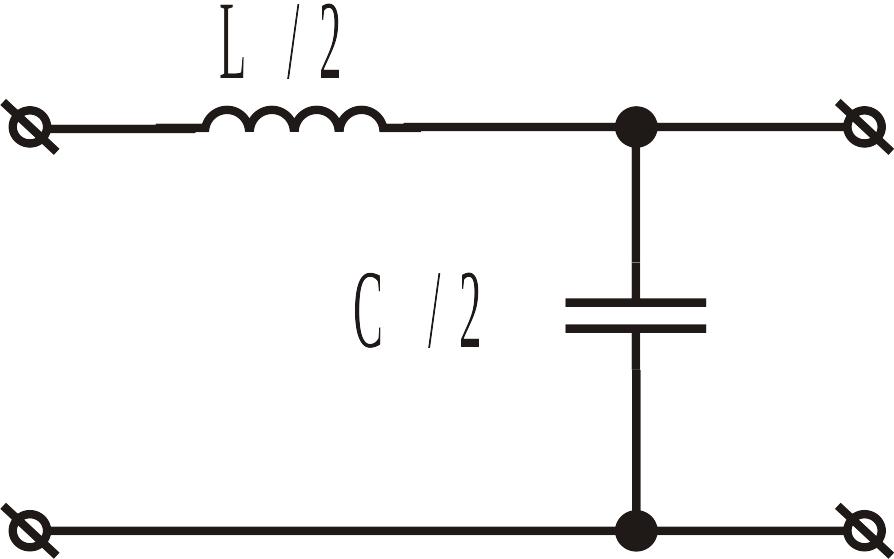
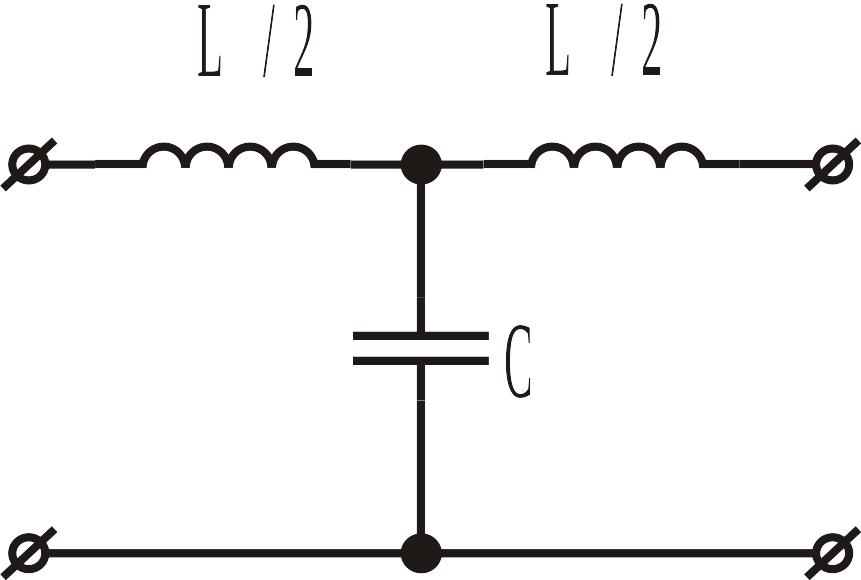
а б в

Рис. ІІ.2.2. Фільтри нижніх частот типу k.

Для ланок k-фільтра

, (ІІ.2.11)

де – хвильовий опір послідовного коливального контуру, який при довільній частоті дорівнює сталій додатній величині.

Згідно з (ІІ.2.5), граничні частоти смуги прозорості дорівнюють:

(ІІ.2.12)

30

Враховуючи, що для фільтра низьких частот

, (ІІ.2.13)

частотні характеристики запишуться у вигляді:

а) в зоні прозорості

; (ІІ.2.14)

б) в зоні згасання

, (ІІ.2.15)

де – відносна частота.

Оскільки

,

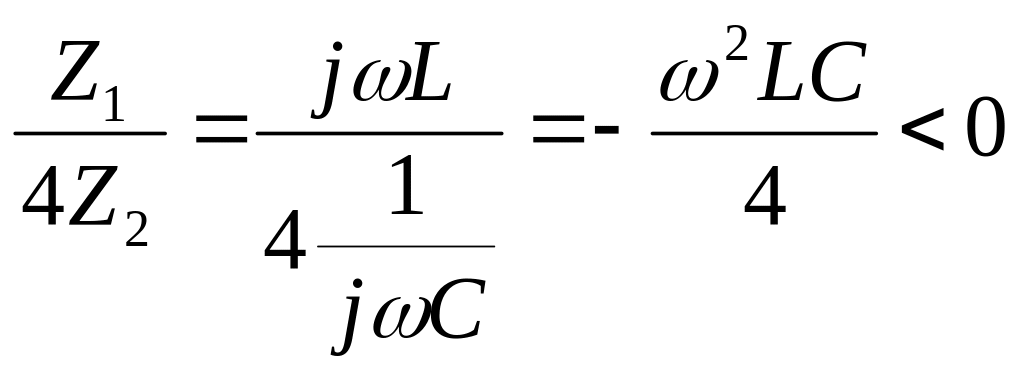то коефіцієнт фази в зоні згасання дорівнює 180⁰.

Характеристичний опір низькочастотного фільтра залежить від його схеми.

Для Т-схеми, з урахуванням того, що поздовжній опір дорівнює , а поперечний – , характеристичний опір запишеться у вигляді:

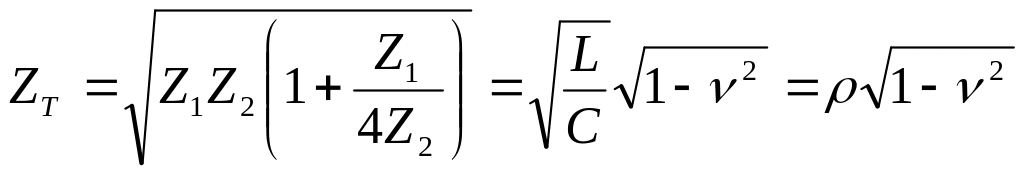. (ІІ.2.16)

31

У зоні пропускання , тому характеристичний опір буде суто активним. У зоні затухання , а значить, характеристичний опір

(ІІ.2.17)

має індуктивний характер.

Для П-схеми, з урахуванням того, що поздовжній опір дорівнює , а поперечний – , характеристичний опір запишеться у вигляді:

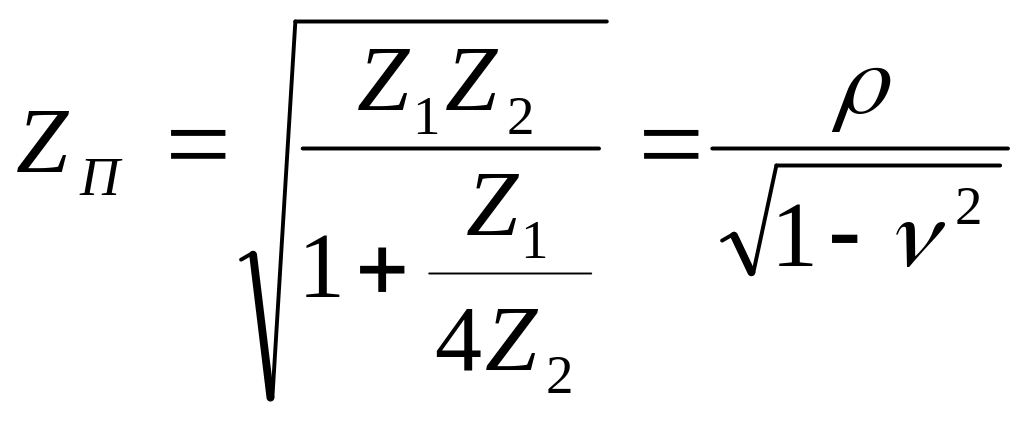. (ІІ.2.18)

У зоні пропускання ( ) цей опір суто активний, а в зоні згасання ( ) – суто ємнісний, тобто

. (ІІ.2.19)

Частотні характеристики фільтра, що розглядається, наведені на рис. ІІ.2.3.

Як випливає з виразів (ІІ.2.16) і (ІІ.2.18), при малих значеннях частот характеристичні опори змінюються мало й близькі до значення . Тому, коли навантаження узгоджено з низькочастотним k-фільтром на частоті , то таке узгодження дійсне в досить широкому діапазоні частот.

Для обчислення параметрів низькочастотного фільтра

32

а

б

Рис. ІІ.2.3.

використовують систему рівнянь

(ІІ.2.20)

33

Звідси одержуємо

, . (ІІ.2.21)

ІІ.2.3.2. Реактивні високочастотні фільтри типу k

Високочастотні фільтри – це такі, які пропускають у навантаження високі частоти, від до . Схеми ВЧ фільтрів наведені на рис. ІІ.2.4.

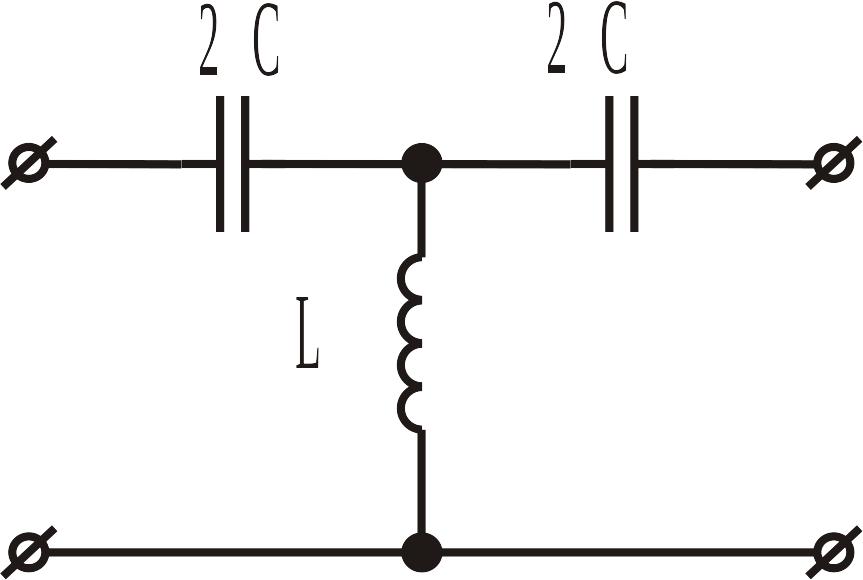
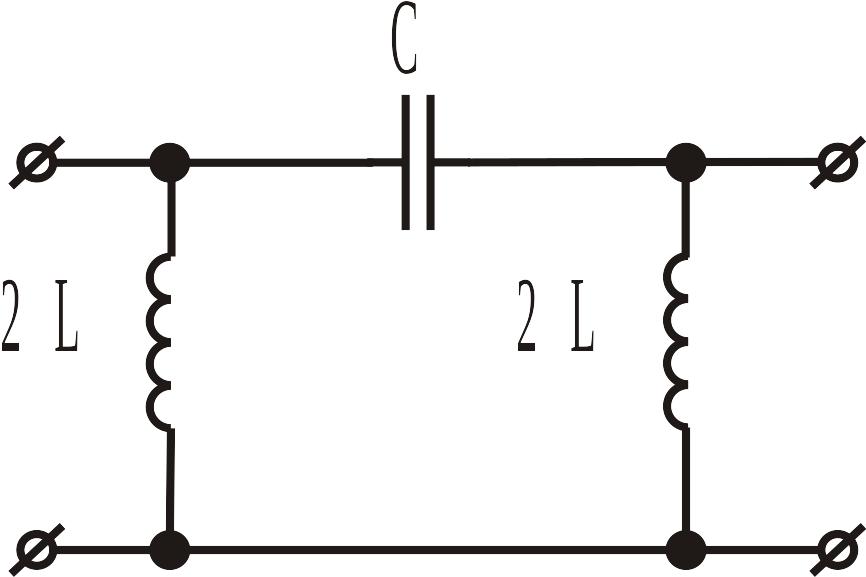
а б в

Рис. ІІ.2.4. Фільтри верхніх частот типу k.

Згідно з (5), граничні частоти смуги прозорості дорівнюють

; (ІІ.2.22)

. (ІІ.2.23)

Частотні характеристики:

а) в зоні прозорості

, (ІІ.2.24)

де – відносна частота ( ).

34

б) в зоні згасання

; ; (ІІ.2.25)

в) характеристичні опори

; (ІІ.2.26)

. (ІІ.2.27)

Частотні характеристики фільтра верхніх частот наведені на рис. ІІ.2.5.

При обчисленні параметрів високочастотних фільтрів задають зону пропускання, тобто , і опір навантаження, який у режимі узгодження при дорівнює характеристичному опору

.

З наведених співвідношень випливає, що

; (ІІ.2.28)

. (ІІ.2.29)

35

а

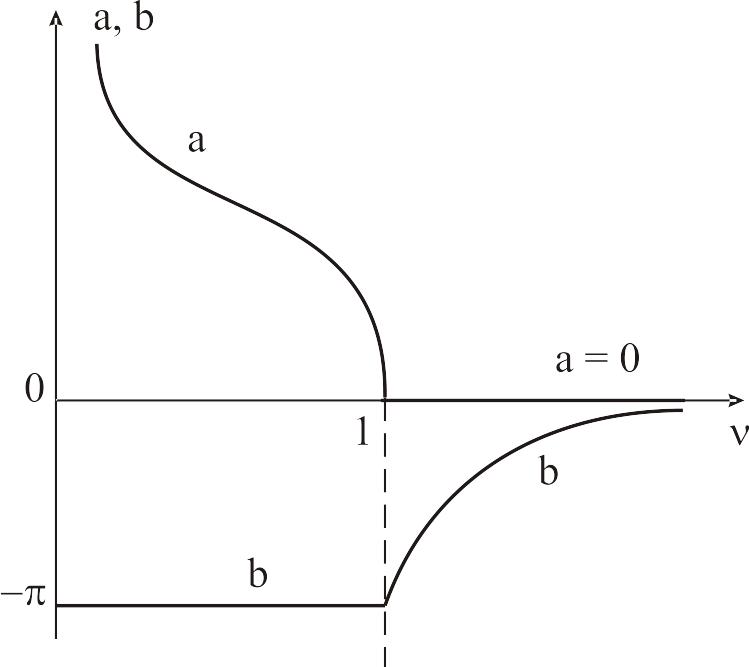
б

Рис. ІІ.2.5 б. Частотні характеристики ВЧФ

ІІ.2.4. Фільтри типу m

Перевагою фільтрів типу k є їхня простота, а також те, що в смузі затримки коефіцієнт згасання в міру віддалення частоти від частоти зрізу неухильно зростає.

36

Недоліки полягають у наступному:

1. Зони пропускання та згасання у фільтрів типу k розділяються недостатньо чітко (різко), тобто крутизна характеристики на межі цих зон недостатня.

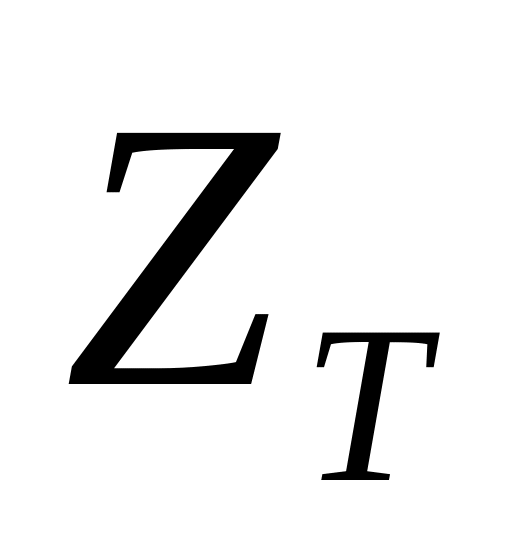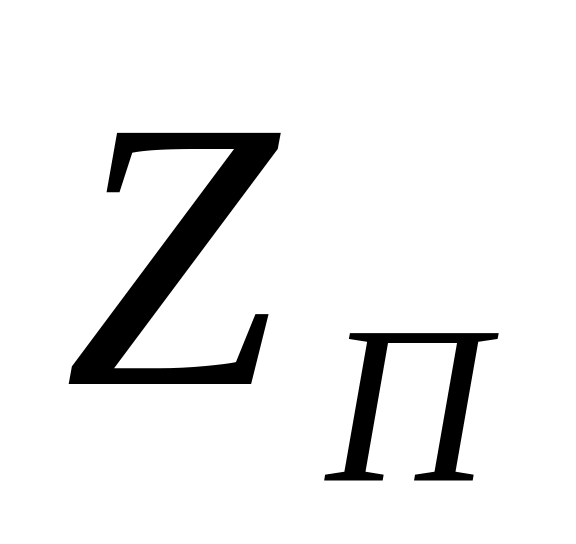2. Характеристичні опори і в зоні пропускання фільтра суттєво залежать від частоти, внаслідок чого узгодити навантаження з фільтром вдається тільки в обмеженій частині смуги пропускання. (Прим. Для НЧФ узгодження здійснюють на частоті , ВЧФ – на частоті ).

Для збільшення крутизни кривої згасання застосовують каскадне з’єднання кількох ланок k-фільтра.

Другий із наведених недоліків усувають шляхом трансформації поздовжньої або поперечної вітки Г-подібної ланки типу k таким чином, щоб одержалась нова Г-подібна ланка з характеристичним опором, який мало змінюється зі зміною частоти в смузі пропускання.

Другий характеристичний опір нового фільтра, який називають фільтром типу m, повинен дорівнювати характеристичному опору вихідної ланки типу k, яку називають прототипом.

Рівність характеристичних опорів нового фільтра й прототипу дозволяє з’єднувати їх узгоджено й утворювати в такий спосіб комбіновані фільтри, які поєднують у собі переваги фільтрів обох типів. Внаслідок того, що Г-подібний прототип має два характеристичні опори, можливі наступні два варіанти утворення m-фільтра.

1. Однаковими залишаються характеристичні опори . Одержану при цьому ланку m-типу називають послідовно-похідною.

2. Однаковими залишаються характеристичні опори . У цьому випадку одержану ланку m-типу називають паралельно-похідною.

Розглянемо перший варіант (рис. ІІ.2.6).

37

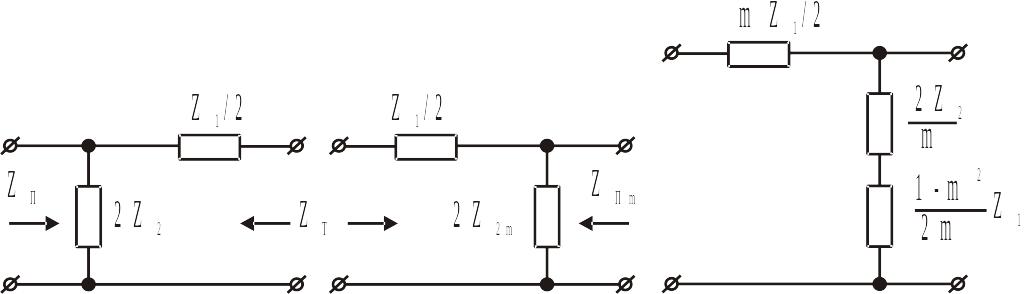
а б в

Рис. ІІ.2.6.Утворення послідовно-похідної ланки типу m.

З умови рівності характеристичних опорів ланок (рис.ІІ.2.6 а і б) випливає:

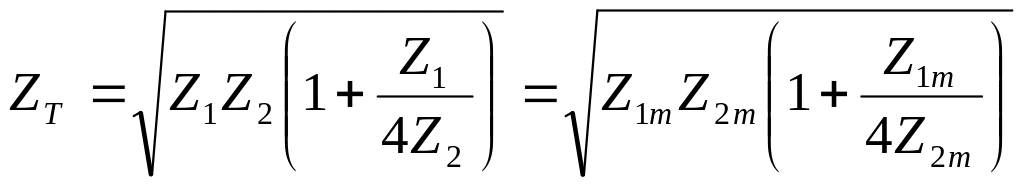. (ІІ.2.30)

Нехай

, (ІІ.2.31)

де

. (ІІ.2.32)

Підстановка (31) в (30) і розв’язання одержаного рівняння відносно дає

. (ІІ.2.33)

З цього виразу видно, що поперечне плече послідовно-похідної Г-подібної ланки типу m складається з двох послідовно з’єднаних опорів і (рис. ІІ.2.6, в).

38

Розглянемо другий варіант утворення Г-подібної ланки типу m (рис. ІІ.2.7).

а б в

Рис. ІІ.2.7. Утворення паралельно-похідної ланки типу m

Виходячи з умови рівності характеристичних опорів, для рис. ІІ.2.7 а і б одержуємо:

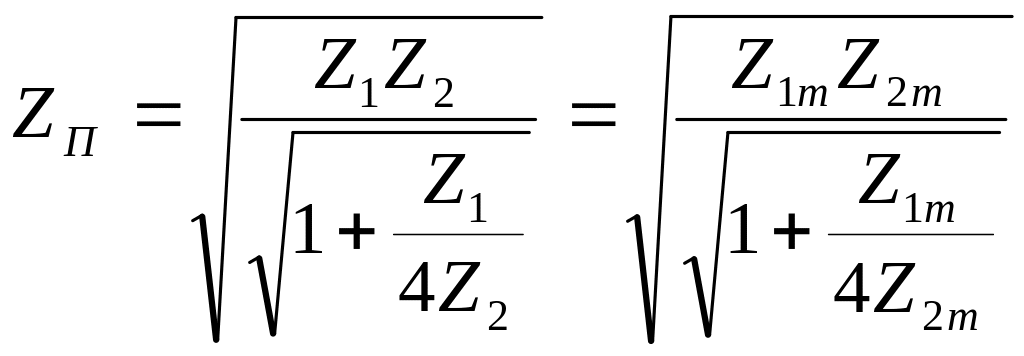. (ІІ.2.34)

Нехай

, . (ІІ.2.35)

Підставляючи (ІІ.2.35) в (ІІ.2.34) і розв’язуючи одержане рівняння відносно , одержимо:

. (ІІ.2.36)

Зі співвідношення провідностей (ІІ.2.36) випливає, що поздовжнє плече Г-подібної ланки типу m складається з опорів і , з’єднаних паралельно (рис. ІІ.2.7, в).

39

Враховуючи (ІІ.2.33) і (ІІ.2.36), для характеристичних опорів (рис. ІІ.2.7) і (рис.ІІ.2.6) одержимо:

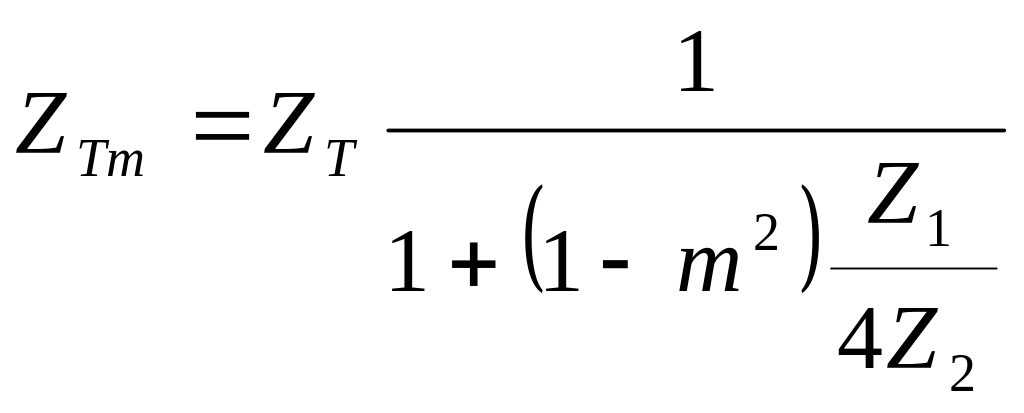; (ІІ.2.37)

. (ІІ.2.38)

Безпосередньо можна перевірити, що

. (ІІ.2.39)

Смуги пропускання фільтрів обох типів також збігаються. Дійсно, на основі (ІІ.2.31) і (ІІ.2.33) або (ІІ.2.35) і (ІІ.2.36) можна одержати наступне співвідношення:

. (ІІ.2.40)

Підставляючи в (ІІ.2.40) умови (ІІ.2.5) для визначення граничних частот (частот зрізу) смуги пропускання, одержимо:

. (ІІ.2.41)

Ці умови відповідають граничним частотам фільтра типу m та ідентичні умовам (ІІ.2.5). Тобто частоти зрізу обох фільтрів дійсно збігаються.

40

ІІ.2.4.1 Низькочастотні фільтри типу m

Конструювання та функціонування фільтрів типу m розглянемо на прикладі низькочастотного фільтра, сформованого за принципом послідовно-похідної ланки (рис. ІІ.2.8).

а б

Рис. ІІ.2.8.Фільтр нижніх частот типу m.

Враховуючи, що

; (ІІ.2.42)

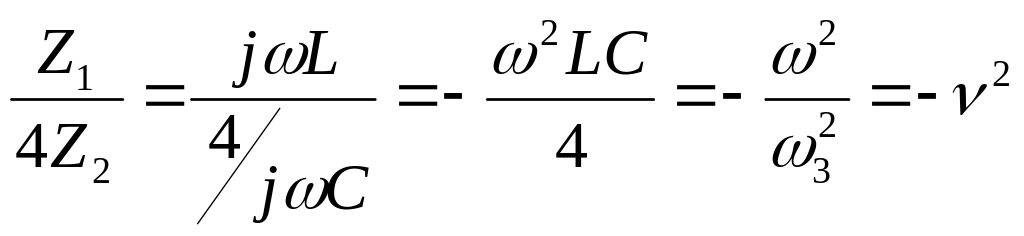; (ІІ.2.43)

; (ІІ.2.44)

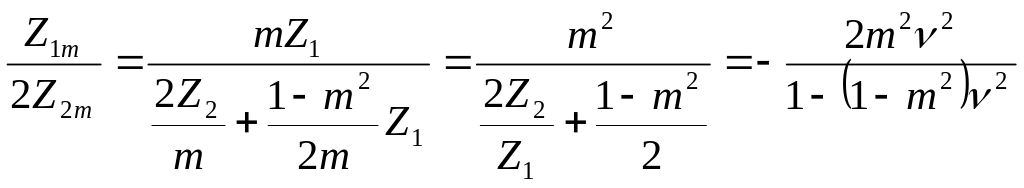;(ІІ.2.45)

для характеристичного опору і коефіцієнта згасання в зоні

41

згасання одержимо наступні співвідношення:

; (ІІ.2.46)

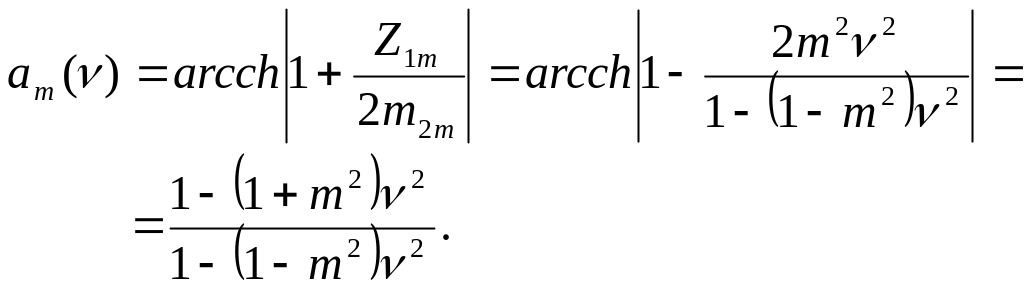(ІІ.2.47)

Частота безмежно великого згасання визначається з умови

, (ІІ.2.48)

звідки одержуємо

(ІІ.2.49)

На рис.ІІ.2.9 зображене сімейство кривих залежності відносних характеристичних опорів або ( ) від параметра , який дорівнює для НЧ фільтрів або для ВЧ (на рисунках позначені та відповідно).

На рис. ІІ.2.10 задане аналогічне сімейство залежностей для коефіцієнта згасання.

42

Рис. ІІ.2.9.

43

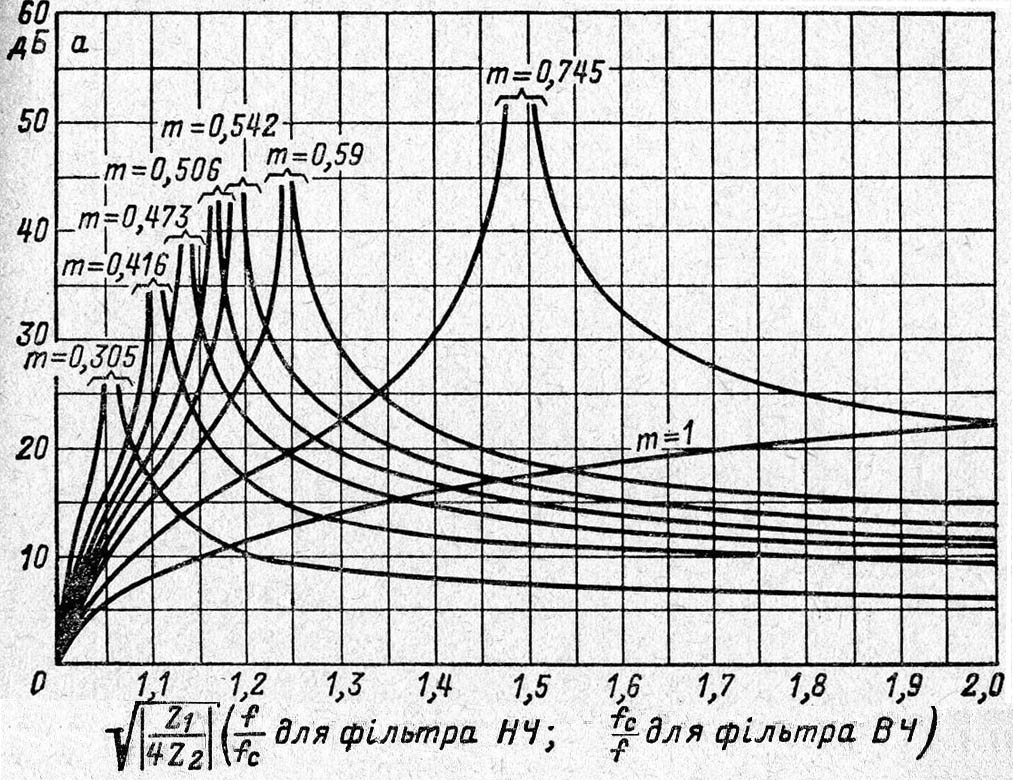
Рис. ІІ.2.10.

ІІ.2.4.2. Фільтри верхніх частот типу m

Утворення ВЧФ типу m з прототипу k і схеми з послідовно-похідною та паралельно-похідною ланками зображено на рисунку ІІ.2.11.

Частота безмежно великого згасання

. (ІІ.2.50)

Частотні характеристики:

; (ІІ.2.51)

44

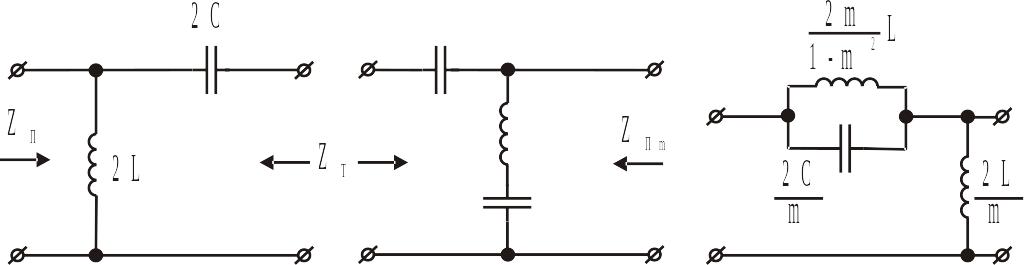
а б в

Рис. ІІ.2.11. Фільтр верхніх частот типу m

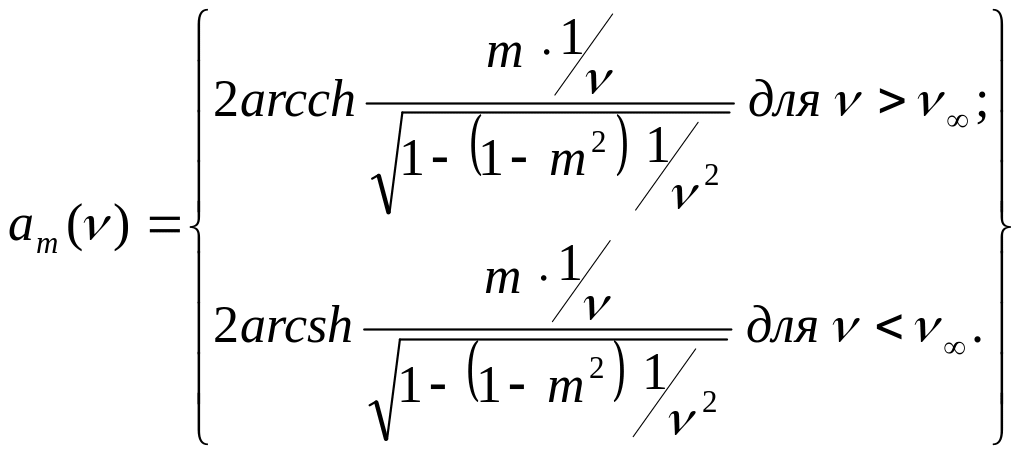(ІІ.2.52)

Частотні характеристики ВЧФ типу m зображено на рисунках ІІ.2.9 і ІІ.2.10.

ІІ.3. Перехідні процеси в лінійних колах із зосередженими ПАРАМЕТРАми

ІІ.3.1. Виникнення перехідних процесів

Усталені процеси в лінійних електричних колах – це процеси, при яких напруги та струми або незмінні в часі (кола постійного струму), або являють собою періодичні функції часу (кола змінного струму).

Встановленню усталеного режиму, відмінного від попереднього, передує, як правило, перехідний процес, при якому напруги та струми змінюються неперіодично.

45

Перехід від одного режиму роботи кола до іншого може бути викликаний зміною параметрів або зміною структури кола. Такі зміни, в загальному випадку, в електротехніці називають комутацією. У схемах комутацію позначають так, як зображено на рис. ІІ.3.1 та рис. ІІ.3.2.

Рис. ІІ.3.1 Рис. ІІ.3.2

Теоретично можна вважати, що комутація в колі здійснюється миттєво. Якщо електричне коло складається тільки з опорів і не містить індуктивностей і ємностей, то перехід від одного усталеного режиму до іншого здійснюється практично миттєво, без витрати часу.

Якщо коло містить хоча б один реактивний елемент (L або С), то новий усталений режим після комутації встановлюється

протягом деякого проміжку часу. Фізично це пояснюється неможливістю миттєвої зміни енергії магнітного поля , що запасається в індуктивному елементі, та енергії електричного поля , що запасається в ємнісному елементі. У протилежному випадку потужність, яка визначається похідною за часом від енергії, в момент комутації досягала би безмежних значень, що фізично неможливо.

В одних випадках перехідні процеси в електричних колах небажані й небезпечні (наприклад при коротких замиканнях в енергетичних системах). В інших випадках перехідний процес являє собою природний нормальний режим роботи кола, як це має місце, наприклад, в радіопередавальних і радіоприймальних колах, системах автоматичного регулювання тощо.

46

Існують різні методи розрахунку перехідних процесів у лінійних електричних колах. Найбільш вживаними є класичний і операторний методи.

ІІ.3.2. Класичний метод

ІІ.3.2.1. Закони комутації та початкові умови

Викладені вище положення про те, що запас енергії магнітного і електричного полів може змінюватись тільки плавно, без стрибків, виражають принцип неперервності в часі потокозчеплення індуктивності й електричного заряду ємності й називаються законами комутації.

Неможливість стрибкоподібної зміни потокозчеплення випливає з того, що інакше на індуктивності з’явилась би безмежно велика напруга , що позбавлено фізичного змісту. Завдяки рівності принцип неперервності потокозчеплення означає: при незмінній L струм і не може змінитися стрибком. Отже, у початковий момент після комутації струм в індуктивності залишається таким самим, яким він був безпосередньо перед комутацією, а потім плавно змінюється.

Аналогічно неможливість стрибкоподібної зміни електричного заряду q випливає з того, що інакше через ємність протікав би безмежно великий струм , що також позбавлено фізичного змісту. Завдяки рівності принцип неперервності електричного заряду означає: при незмінній С напруга не може змінитися стрибком.

Як правило, вважають, що комутація відбувається в момент часу t=0. Тоді струм в індуктивності й напруга на ємності в момент часу безпосередньо перед комутацією позначаються

47

та відповідно, а в початковий момент після комутації – через та .

Закони комутації тоді можна аналітично записати в наступному вигляді:

(ІІ.3.1)

Значення струму в індуктивності й напруги на ємності в момент комутації називають незалежними початковими умовами.

ІІ.3.2.2. Усталений (вимушений) і вільний режими

У загальному випадку аналіз перехідного процесу в лінійному колі із зосередженими параметрами R, L, C i M зводиться до розв’язання лінійних неоднорідних диференційних рівнянь, які виражають закони Кірхгофа. Ці рівняння являють собою лінійну комбінацію напруг, струмів, їх перших похідних і інтегралів за часом.

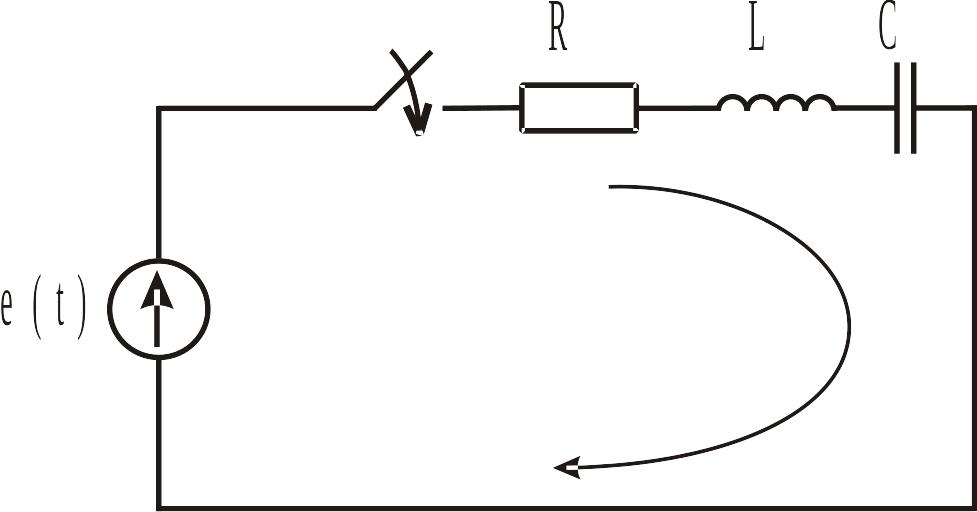
Рис. ІІ.3.3

Для схеми на рис. ІІ.3.3 вираз, записаний за другим законом Кірхгофа, являє собою наступне інтегро-диференційне

48

рівняння:

. (ІІ.3.2)

Це рівняння після диференціювання за часом зводиться до неоднорідного диференційного рівняння другого порядку

. (ІІ.3.3)

Як відомо, загальний розв’язок такого рівняння дорівнює сумі частинного розв’язку неоднорідного рівняння й загального розв’язку однорідного рівняння.

Частинний розв’язок описує зміни в часі струму в усталеному режимі, який встановлюється в колі після комутації й характер якого визначається зовнішнім джерелом. Цей розв’язок називають вимушеною складовою перехідного струму (напруги).

Загальний розв’язок однорідного рівняння фізично визначає поведінку кола при заданих початкових умовах і відсутності джерел електричної енергії. Функції, які визначаються загальним розв’язком, називаються вільними складовими (струмів, напруг).

Для схеми рис. ІІ.3.1 однорідне рівняння має вигляд

; (ІІ.3.4)

йому відповідає наступне характеристичне рівняння:

. (ІІ.3.5)

49

Якщо корені характеристичного рівняння позначити через і , то загальний розв’язок запишеться у вигляді:

, (ІІ.3.6)

де і – константи інтегрування, які визначаються з початкових умов.

Повний перехідний струм у колі дорівнює сумі вимушеної й вільної складових

. (ІІ.3.7)

Розглянутий підхід до визначення перехідних функцій, в основі якого лежить формула (ІІ.3.7), називають класичним методом.

ІІ.3.2.3. Алгоритм розрахунку перехідних процесів класичним методом

1. З докомутаційної схеми визначаємо незалежні початкові умови, тобто струми в індуктивностях і напруги на ємностях безпосередньо до комутації.

2. Перехідні струми (напруги) шукаємо у вигляді суми вимушених і вільних складових, тобто

, (ІІ.3.8)

де k – номер вітки.

3. Вимушені складові знаходимо, розраховуючи післякомутаційну схему в усталеному режимі.

4. Вільні складові шукаємо у вигляді (ІІ.3.9)

50

, (ІІ.3.9)

де n – порядок характеристичного рівняння;

– константи інтегрування;

– корені характеристичного рівняння.

4.1. Характеристичне рівняння знаходимо за наступним формальним алгоритмом:

а) знаходимо комплексний опір для післякомутаційної схеми;

б) формально у виразі замінюємо на , тобто знаходимо вираз для ;

в) прирівнюємо до нуля. Це й буде характеристичне рівняння для даної задачі. Розв’язавши його, знайдемо корені .

4.2. Для знаходження констант інтегрування складаємо систему рівнянь (ІІ.3.10), а знаходимо з розрахунків пункту 3 даного алгоритму.

(ІІ.3.10)

51

Для знаходження складаємо систему рівнянь для післякомутаційної схеми за методом законів Кірхгофа й записуємо цю систему рівнянь для моменту комутації (t=0) з урахуванням незалежних початкових умов, одержаних в пункті 1 алгоритму.

Розв’язавши систему рівнянь (ІІ.3.10), знаходимо константи інтегрування, а значить, і вільні складові перехідних струмів.

5. Записуємо остаточні вирази для перехідних струмів згідно з формулою (ІІ.3.8).

ІІ.3.3. Операторний метод

ІІ.3.3.1. Перетворення Лапласа

Громіздкість процедури знаходження констант інтегрування з початкових умов у ряді випадків суттєво ускладнює розрахунок перехідних процесів класичним методом. З ускладненням електричних схем і відповідним зростанням порядку диференційних рівнянь ці труднощі збільшуються.

Усувається даний недолік застосуванням для розрахунку перехідних процесів так званого операторного методу, ідея якого полягає в тому, що з області функцій дійсної змінної розв’язок переноситься в область функцій комплексної змінної , де операції набувають простішого вигляду, а саме: замість диференційних чи інтегро-диференційних рівнянь одержуються алгебраїчні рівняння. Після розв’язання алгебраїчних рівнянь відбувається зворотний перехід в область функцій дійсної змінної.

В основі операторного методу лежить перетворення Лапласа, яке функції часу ставить у відповідність її операторне зображення за допомогою наступного інтеграла:

52

, (ІІ.3.11)

де – комплексна частота.

Відповідність між операторним зображенням і його оригіналом записують так:

. (ІІ.3.12)

Для однозначної відповідності функція повинна відповідати умовам Дирихле, тобто бути неперервною в області визначення, мати скінченну кількість розривів першого роду й скінченну кількість точок екстремуму. Крім того, необхідно, щоб при t>0 виконувалась нерівність , де А і  - деякі додатні числа. Це означає, що повинна бути забезпечена можливість такого вибору А і , щоб модуль функції зростав повільніше від функції . Усі реальні фізичні величини електричних кіл відповідають таким умовам. І, нарешті, щоб інтеграл Лапласа мав скінченне значення, необхідно припустити, що >.

ІІ.3.3.2. Операторне зображення деяких функцій

1. Операторне зображення похідної

. (ІІ.3.13)

2. Операторне зображення похідної другого порядку

. (ІІ.3.14)

53

3. Операторне зображення похідної n-го порядку

.( ІІ.3.15)

4. Операторне зображення напруги на індуктивному елементі

. (ІІ.3.16)

5. Операторне зображення інтеграла

(ІІ.3.17)

6. Операторне зображення константи

А = const (ІІ.3.18)

7. Операторне зображення напруги на ємності

(ІІ.3.19)

8. Операторні зображення експонент

а) (ІІ.3.20)

54

б) (ІІ.3.21)

в) (ІІ.3.22)

г) (ІІ.3.23)

9. Операторні зображення гармонійних функцій часу

а) (ІІ.3.24)

б) (ІІ.3.25)

ІІ.3.3.3. Закон Ома в операторній формі

Розглянемо перехідний процес у вітці з ненульовими початковими умовами.

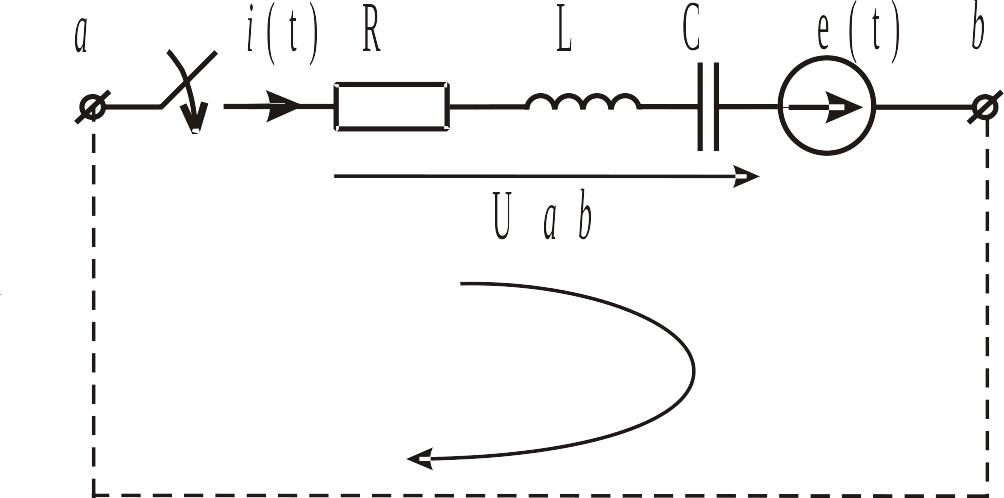
Рис. ІІ.3.4

55

Розглянемо уявний контур (пунктирна лінія) і запишемо другий закон Кірхгофа для нього:

(ІІ.3.26)

З урахуванням співвідношень (ІІ.3.11), (ІІ.3.16) і (ІІ.3.19) це рівняння перепишеться в наступній операторній формі:

. (ІІ.3.27)

Звідки одержуємо

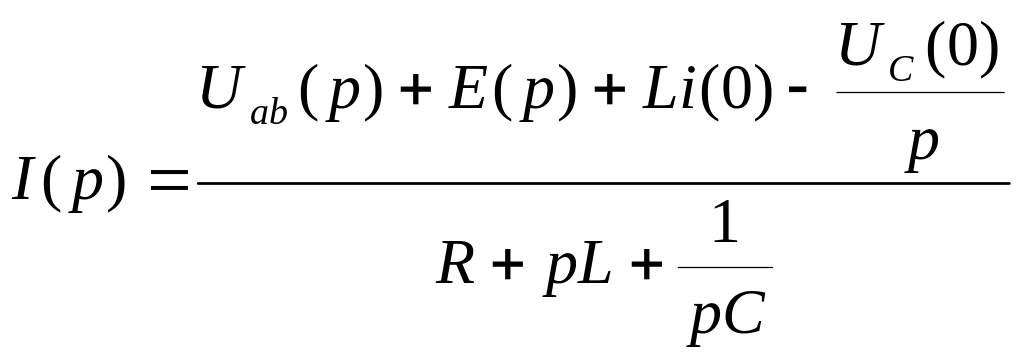, (ІІ.3.28)

, (ІІ.3.29)

де – операторний опір вітки;

– внутрішня операторна ЕРС індуктивності;

– внутрішня операторна ЕРС ємності.

Рівняння (ІІ.3.28) є законом Ома в операторній формі для розглянутої вітки.

Згідно з (ІІ.3.28), операторний струм дорівнює відношенню алгебраїчної суми операторної напруги на вітці, зовнішніх і внутрішніх операторних ЕРС до операторного опору вітки.

56

Операторну схему заміщення вітки, згідно з (ІІ.3.28), можна зобразити в наступному вигляді:

Рис. ІІ.3.5

Напрямок внутрішньої ЕРС завжди збігається з умовно-додатним напрямком операторного струму , напрямок – завжди протилежний.

ІІ.3.3.4. Закони Кірхгофа в операторній формі

а) Перший закон Кірхгофа: алгебраїчна сума операторних струмів у довільному вузлі електричного кола дорівнює нулеві.

. (ІІ.3.30)

Приклад:

Рис. ІІ.3.6

57

Для вузла а (рис.ІІ.3.6) вираз (ІІ.3.30) запишетться у вигляді:

. (ІІ.3.31)

б) Другий закон: алгебраїчна сума операторних напруг на пасивних ділянках довільного контуру електричного кола дорівнює алгебраїчній сумі зовнішніх і внутрішніх ЕРС, що діють у цьому контурі.

Приклад.

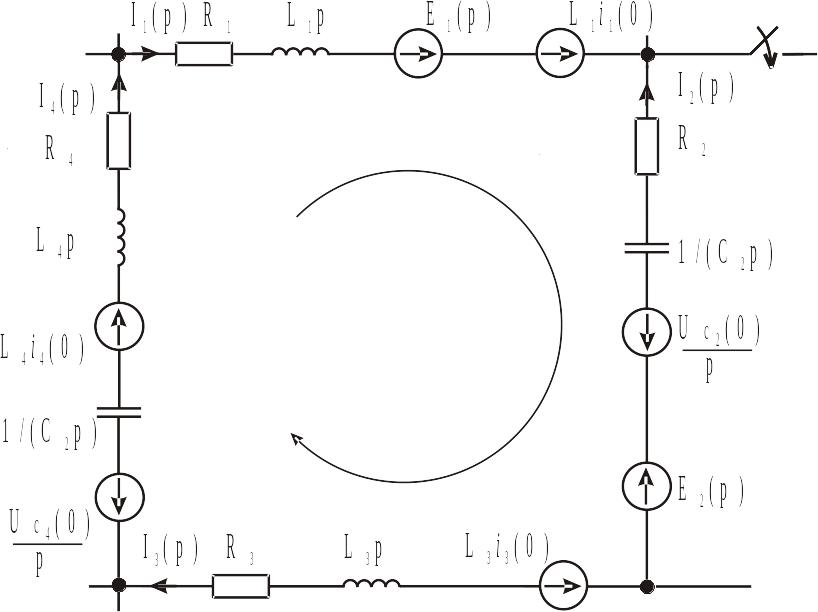
Рис. ІІ.3.7

Розглянемо операторну схему заміщення деякого контуру електричної схеми (рис. ІІ.3.7), в якій має місце перехідний процес із ненульовими початковими умовами.

58

Другий закон Кірхгофа в операторній формі запишеться у вигляді

де

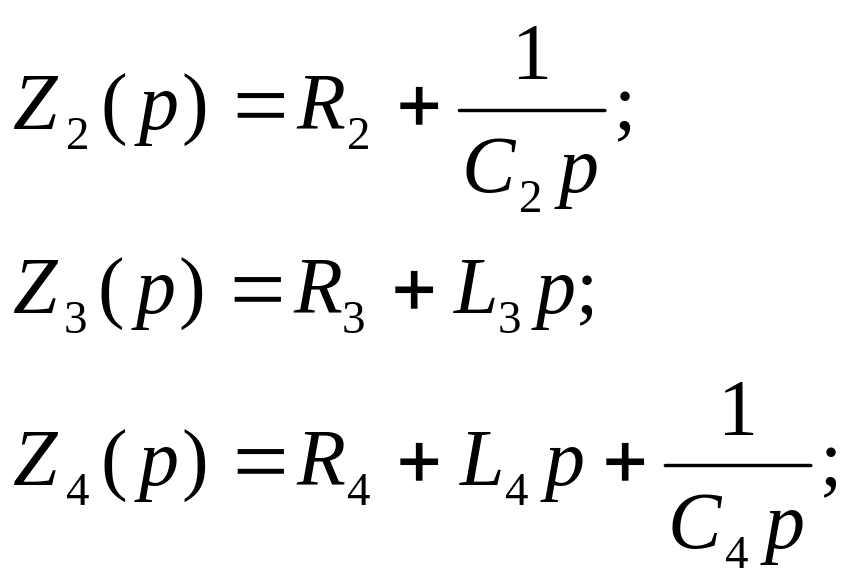
– алгебраїчна сума зовнішніх операторних ЕРС;

– алгебраїчна сума внутрішніх операторних ЕРС.

ІІ.3.3.5. Алгоритм операторного методу розрахунку перехідних процесів

1. З докомутаційної схеми визначаємо незалежні початкові умови, тобто струми на індуктивностях і напруги на ємностях безпосередньо до комутації.

2. Задану післякомутаційну схему замінюємо операторною схемою заміщення. При цьому елементи замінюються на ; а елементи та - на та відповідно.

Ненульовим початковим умовам в операторній схемі заміщення ставляться у відповідність внутрішні джерела.

59

3. Розраховуємо операторну схему одним із методів розрахунку кіл постійного струму. В результаті розрахунку одержуємо операторні струми (напруги), які мають вигляд відношення поліномів за степенями змінної , тобто

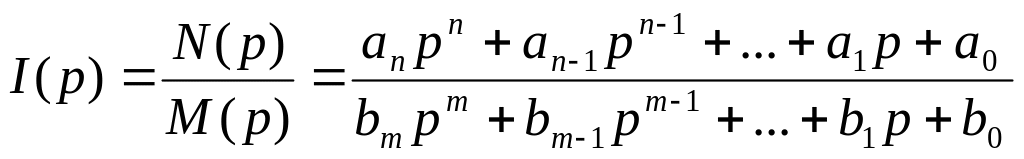. (ІІ.3.33)

4. Операторним струмам (напругам) ставимо у відповідність їхні оригінали або за допомогою таблиць операторних зображень функцій часу, або за допомогою наступної формули розкладу

, (ІІ.3.34)

де – корені рівняння , тобто корені знаменника виразу (ІІ.3.33),

– значення похідної при всіх коренях .

60