
Омский государственный технический университет
Кафедра
«Средства связи»
Лабораторная работа №1-8 по курсу
«Теория электрической связи»
«ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ДЕТЕРМИНИРОВАННЫХ И КВАЗИСЛУЧАЙНЫХ ПРОЦЕССОВ»
1
Выполнил: студент
группы РП-210
Китов Евгений
Проверил: с.н.с., д.т.н.,
доцент Хазан В.Л.
Омск 2002
ЦЕЛЬ РАБОТЫ:
Ознакомление с методом корреляционного анализа и практическое определение корреляционных функций детерминированных сигналов (видеоимпульсов и радиоимпульсов), а также корреляционных функций квазислучайных дельта-корелированных и марковских процессов.
Теоретические сведения.
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ДЕТЕРМИНИРОВАННЫХ И КВАЗИСЛУЧАЙНЫХ ПРОЦЕССОВ
Функция корреляции.
Для определения степени похожести двух процессов u1(t) и u2(t) служит функция корреляции:
![]() (1-8.1)
(1-8.1)
Здесь t -время задержки сигнала u2(t).
Н а
рис. 1-8.1 приведена блок-схема коррелометра,
алгоритм которого соответствует
(1-8.1).
а
рис. 1-8.1 приведена блок-схема коррелометра,
алгоритм которого соответствует
(1-8.1).
Рис. 1-8.1
Здесь ЛЗ - линия задержки. Роль интегратора при практической реализации коррелометра может играть фильтр низких частот (ФНЧ).
Первый вариант входных воздействий (u1(t) - на вход №1, а u2(t - ) - на вход №2 перемножителя) полностью соответствует формуле (1-8.1). Второму варианту входных воздействий (u1(t - ) - на вход №2, а u2(t) - на вход №1 перемножителя) соответствует формула:
![]() (1-8.2)
(1-8.2)
Таким образом функция корреляции существует на всей оси t времени задержки от t = - ∞ до t = + ∞.
Если u1(t) и u2(t) два различных процесса, то функцию корреляции для определенности часто называют взаимокорреляционной функцией (ВКФ).
Если u1(t) = u2(t) = u(t), как в случае, изображенном на рис. 1-8.2, то функцию корреляции называют автокорреляционной функцией (АКФ). АКФ характеризует похожесть функции u(t) и ее копии, задержанной на различное время t. В отличие от предыдущего случая смена местами самой функции и ее копии не придает нового качества результату на выходе интегратора. Поэтому функция автокорреляции в отличие от взаимокорреляционной функции является функцией четной.
Т.е. Вu(t) = Вu(-t), но Bu1u2(t) Bu1u2(-t).

Рис. 1-8.2
Энергетический спектр и АКФ сигнала связаны преобразованием Фурье:
![]() (1-8.3)
(1-8.3)
![]()
![]() (1-8.4)
(1-8.4)
Из (1-8.1) следует, что для t = 0:
![]()
Таким образом максимальное значение АКФ равно энергии сигнала.
Практических примеров использования функций корреляции достаточно много.
Например, коэффициенты ряда Фурье am и bm с точностью до множителя являются не чем иным, как значениями ВКФ при t = 0 разлагаемой в ряд Фурье периодической последовательности и гармонических колебаний (соответственно косинуса и синуса) с частотой m/T.
Другой пример: часто при определении энергетического спектра процесса удобнее вначале измерить АКФ, а затем с помощью преобразования Фурье найти собственно энергетический спектр.
Далее ограничимся рассмотрением только АКФ процессов.
Корреляционные функции детерминированных сигналов.
Р ассмотрим
наиболее простой случай, когда сигнал
- прямоугольный импульс U(t). На рис. 1-8.3
приведено построение корреляционной
функции Bu(t)
(рис. 1-8.3(d)) для одиночного прямоугольного
импульса (рис. 1-8.3(а)). На рис. 1-8.3(b) изображен
задержанный на время t прямоугольный
импульс U(t-t), а на рис. 1-8.3(с) результат
перемножения U(t)U(t-t).
Заштрихованная площадь на рис. 1-8.3(с)
соответствует численному значению
функции корреляции прямоугольного
импульса. Сама функция корреляции
прямоугольного импульса имеет форму
равностороннего треугольника.
ассмотрим
наиболее простой случай, когда сигнал
- прямоугольный импульс U(t). На рис. 1-8.3
приведено построение корреляционной
функции Bu(t)
(рис. 1-8.3(d)) для одиночного прямоугольного
импульса (рис. 1-8.3(а)). На рис. 1-8.3(b) изображен
задержанный на время t прямоугольный
импульс U(t-t), а на рис. 1-8.3(с) результат
перемножения U(t)U(t-t).
Заштрихованная площадь на рис. 1-8.3(с)
соответствует численному значению
функции корреляции прямоугольного
импульса. Сама функция корреляции
прямоугольного импульса имеет форму
равностороннего треугольника.
Рис. 1-8.3
На рис. 1-8.4 показаны функции корреляции для некоторых других видов сигналов:
(а) - гармонического;
(b) - радиоимпульса;
(с) - пачки прямоугольных импульсов.
АКФ гармонического сигнала является также гармонической функцией (косинусом), имеющей такой же период как и сам сигнал. АКФ радиоимпульса имеет период несущей и огибающую, которая по форме является АКФ огибающей радиоимпульса. АКФ пачки прямоугольных импульсов состоит из отдельных компонентов, каждый из которых имеет треугольную форму, соответствующую АКФ одиночного прямоугольного импульса.
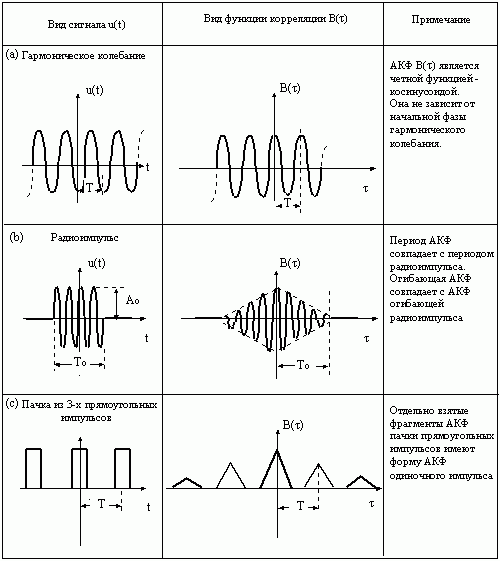
Рис. 1-8.4
Корреляционные функции случайных сигналов.
Если на вход коррелометра, блок-схема которого изображена на рис. 1-8.2 ,подать случайный эргодический процесс u(t) (эргодическим считается случайный процесс, если усреднение по множеству реализаций эквивалентно усреднению по времени), то результатом измерений будет ковариационная функция этого случайного процесса: Ku(t) = M[u(t)u(t - )], где М[x] - математическое ожидание (МО) х. Чтобы измерить корреляционную функцию случайного процесса Ru(t), необходимо в соответствии с алгоритмом:
Ru() = M[(u(t) – M[u])(u(t - ) – M[u])] (1-8.6)
определить МО произведения только случайных составляющих процесса u(t) (без его матожидания M[u]), отсчеты которых взяты с интервалом времени t. Если случайный процесс в достаточной степени высокочастотный, то для получения его функции корреляции достаточно последовательно с входом коррелометра включить емкость, которая пропустит через себя на входы перемножителя и линии задержки только колебательный компонент случайного процесса. На рис. 1-8.5 изображена блок-схема такого рода коррелометра.

Рис. 1-8.5
R(0) по определению является дисперсией процесса, т. е., если u(t)- напряжение, то R(0)- его средняя мощность, выделяемая в сопротивлении 1 Ом.
Часто используют нормированную корреляционную функцию (коэффициент корреляции): r(t) = R(t)/R(0). Очевидно, что всегда модуль r(t) меньше, или равен единице.
Согласно теореме Винера –Хинчина, ковариационная функция случайного процесса Кu(t) и его средняя спектральная плотность мощности Wu() связаны преобразованиями Фурье:
 ;
;
![]() (1-8.7)
(1-8.7)
Для случайного процесса с нулевым средним значением:
![]() ;
;
![]() (1-8.8)
(1-8.8)
Таким образом, чем шире спектр случайного процесса, тем меньше интервал корреляции, и наоборот - чем больше интервал корреляции, тем уже спектр процесса. Для "белого шума" с равномерной средней спектральной плотностью мощности имеем:
![]() (1-8.9)
(1-8.9)
Следовательно корреляционная функция "белого шума" является -функцией. Такого рода процессы называются -коррелированными.
ХОД РАБОТЫ.
