Омский государственный технический университет

Кафедра

«Средства связи»

Лабораторная работа №1-7 по курсу

«Теория электрической связи»

«ФОРМИРОВАНИЕ МАРКОВСКОГО СЛУЧАЙНОГО ПРОЦЕССА С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ»

100000000000000000000000000000000000000000000

Выполнил: студент

группы РП-210

Китов Евгений

Проверил: с.н.с., д.т.н.,

доцент Хазан В.Л.

Омск 2002

ЦЕЛИ РАБОТЫ:

1. Ознакомление с методом формирования марковского нормального случайного процесса с заданными параметрами:

• среднеквадратическим отклонением (СКО);

• математическим ожиданием (МО);

• коэффициентом корреляции R.

2. Изучение методики построения гистограмм случайных процессов.

Теоретические сведения.

ИМИТАЦИОННАЯ МОДЕЛЬ МАРКОВСКОГО НОРМАЛЬНОГО СЛУЧАЙНОГО ПРОЦЕССА

Нормальный (гауссовский) случайный процесс.

Нормальным (гауссовским) законом распределения вероятностей описываются многие случайные (стохастические) явления. Например, последовательность мгновенных значений шума U_ш с математическим ожиданием (МО) U_о и среднеквадратическим отклонением (СКО) S, которая изображена на рис. 1-7.1(a), описывается нормальным законом с плотностью распределения вероятностей p(U_ш):

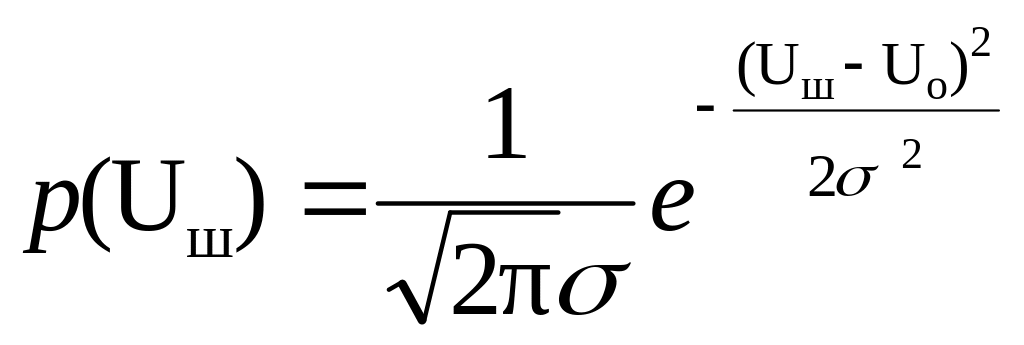(1-7.1)

График плотности распределения вероятностей (1-7.1) изображен (c поворотом на 90^o) на рис. 1-7.1(b).

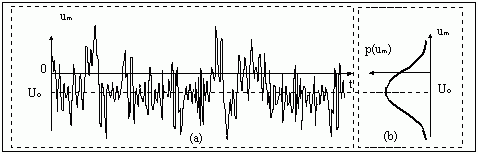
Рис. 1-7.1

Если у случайного процесса МО = 0, то он называется центрированным. Если у процесса СКО = 1, то такой процесс называется нормированным.

Широкополосные случайные процессы имеют очень узкую функцию корреляции и могут приближенно считаться дельта-коррелированными (некоррелированными) процессами. У таких процессов соседние отсчеты не зависят друг от друга и могут отличаться на любую величину в соответствии с имеющими место законами распределения вероятностей. Узкополосные случайные процессы являются коррелированными. Соседние отсчеты у таких процессов отличаются друг от друга тем меньше, чем больше коэффициент корреляции этих процессов. Марковские процессы являются коррелированными процессами.

Имитационная модель марковского процесса.

Случайный процесс U_m(t) называется марковским (процессом без последствия), если для любого момента времени t_i вероятность реализации значения отсчета этого процесса U_m(t_i) зависит только от значения отсчета U_m(t_i - dt), которое было реализовано в предшествующий момент времени t = t_i - dt.

Коэффициент корреляции марковского нормального случайного процесса R зависит следующим образом от времени корреляции T_o и интервала между отсчетами dt:

R(dt) = exp(-dt/T_o) (1-7.2)

В отличие от коррелированных случайных процессов, процессы, у которых коэффициент корреляции равен нулю (например, у "белого" шума) называют дельта-коррелированными. Если отсчеты какого-либо коррелированного случайного процесса брать через интервалы времени dt во много раз превышающими его время корреляции (dt >> To), то последовательность такого рода отсчетов будет представлять собой дельта-коррелированный процесс, так как корреляционная зависимость между этими отсчетами будет отсутствовать.

Если имеется дельта-коррелированный (R = 0), центрированный (МО = 0) и нормированный(СКО = 1) нормальный (гауссовский) процесс U(t), то марковский процесс U_m(t) с заданными параметрами (МО, СКО и R(dt)) может быть легко сформирован с использованием следующего алгоритма:

U_m(t) = [U_m(t – dt) – MO]  R(dt) + CKO  U(t) K + MO (1-7.3)

Н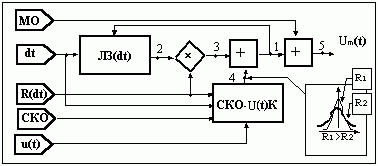 а рис. 1-7.2 приведена блок-схема математической модели, которая соответствует алгоритму (1-7.3).

Рис. 1-7.2

На указанном рисунке дополнительно обозначено: ЛЗ(dt) - линия задержки на время dt; x - умножитель; + - сумматор.

Операция CKOU(t)К для процесса в точке 4 рис. 1-7.2 должна удовлетворять условию сохранения СКО марковского процесса, т. е. на сумматор необходимо подавать долю дельта-коррелированного процесса, которая оставляла бы неизменным мощность (дисперсию) марковского процесса.

Это условие выполняется, если удовлетворяется равенство:

[R(dt)]² + K² = 1 (1-7.4)

Из (1-7.3) следует, что

K = {1 – [R(dt)]²}^1/2 (1-7.5)

На рис. 1-7.2 для точки 4 в виде отдельного фрагмента приведены распределения плотности вероятности дельта-коррелированного процесса, подаваемого на сумматор, в случае больших (тонкая линия) и меньших (толстая линия) значений коэффициента корреляции марковского процесса. Если принять значение коэффициента корреляции R равным нулю (в точке 3 рис. 1-7.2 процесс исчезает), то К = 1 и марковский процесс вырождается в дельта-коррелированный с заданным СКО и МО:

U_m(t) = СКО  U(t) + МО

На рис. 1-7.3 приведены результаты одного цикла последовательности действий в пронумерованных точках блок-схемы, изображенной на рис. 1-7.2.

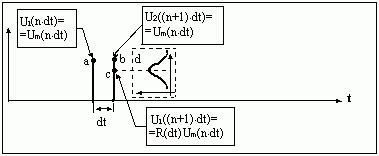
Рис. 1-7.3

Рассмотрим подробнее ход цикла, изображенного на рис. 1-7.3. Точка (a) на этом рисунке соответствует значению отсчета случайного процесса взятого в точке (1) рис. 1-7.2 в некоторый момент времени ndt. Этот отсчет задерживается линией задержки на время dt и точка (b) соответствует значению отсчета в точке (2) рис. 1-7.2 в момент времени (n+1)dt. Точка (с) соответствует значению отсчета процесса на выходе перемножителя в точке (3) рис 1-7.2. Точка (с) всегда будет находиться ниже точки b, так как коэффициент корреляции R меньше единицы. Фрагмент (d) рис. 1-7.3 характеризует закон распределения отсчетов дельта-коррелированного процесса в точке (4) рис.1-7.2, которые поступают на сумматор и прибавляются к уменьшенному в R раз марковскому процессу на выходе перемножителя в точке (3). Так как дельта-коррелированный процесс может принимать как положительные, так и отрицательные значения, то по отношению к точке (с) рис. 1-7.3 следующая точка, которая соответствует точке (1) рис. 1-7.2 и точке (а) рис. 1-7.3 может отклоняться от предыдущего значения как в сторону увеличения, так и в сторону уменьшения. Таким образом изменение значений процесса в точке (1) рис. 1-7.2 могут происходить случайным образом последовательно как в положительной, так и в отрицательной полуплоскости и периодически переходить из одной полуплоскости в другую. Регулярное возвращение к нулевому уровню обусловлено тем, что на каждом рассмотренном цикле происходит умножение задержанного отсчета на коэффициент корреляции, значение которого меньше единицы. Скорость флуктуаций в марковском процессе обусловлена коэффициентом корреляции R и будет тем большей, чем меньше значение R.

Подводя итог вышеизложенному, можно утверждать, что для формирования отсчетов марковского случайного процесса U_m(ndt), взятых с дискретностью dt необходимо иметь дельта-коррелированный (R = 0), центрированный(МО = 0) и нормированный(СКО = 1) нормальный (гауссовский) процесс U(ndt), а также задавать требуемые значения следующих параметров марковского процесса: МО, СКО, T_o и dt. При этом коэффициент корреляции процесса определяется по формуле (1-7.2).

ИМИТАЦИОННАЯ МОДЕЛЬ ДЕЛЬТА-КОРРЕЛИРОВАННОГО И ЦЕНТРИРОВАННОГО НОРМАЛЬНОГО (ГАУССОВСКОГО) ПРОЦЕССА.

Известно, что если в полярных координатах фаза случайного вектора распределена равномерно в пределах от 0 до 2 радиан, а модуль этого вектора распределен по закону Релея, то в декартовых координатах проекции этого вектора распределены по нормальному закону.

Н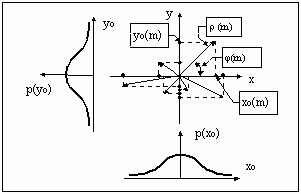 а рис. 1-7.4 показано семейство случайных векторов и распределения их проекций x_o(n) и y_o(n) соответственно на оси абсцисс и ординат.

Рис. 1-7.4

Получение семейства такого рода случайных векторов в любом требуемом количестве не представляет каких-либо проблем.

Для определения фазы каждого случайного вектора и для определения его модуля требуется по одному случайному числу, которые поступают от генератора случайных чисел (ГСЧ) и имеют равномерное распределение от 0 до 1. Примем, что нечетные номера случайных чисел используются для получения фаз, а четные номера - для получения модулей случайных векторов.

Алгоритм определения фазы j(m) m-го вектора при наличии случайного числа z(2n-1), очевиден:

(m) = 2  z(2n - 1) (1-7.6)

Что касается алгоритма определения распределенного по закону Релея модуля вектора r(m), то он требует нелинейных функциональных преобразований случайного числа z(2n). Действительно, числа z(2n) имеют равномерное распределение p(z) = 1 при 0<z<1 и p(z) = 0 при остальных значениях z. Поставим задачу получения числа r(m), имеющим распределение Релея, при наличии равномерно-распределенного числа z(2n).

Закон Релея описывается выражением:

p() = (/²)exp(²/2²) (1-7.7)

При нелинейном преобразовании случайных чисел z(2n) должно выполняться следующее условие: - p(z)dz = p(r) dr (минус перед левой частью равенства не играет какой-либо существенной роли, т. к. говорит лишь о знаке приращения dz). Интегрируя это уравнение, при S = 1 имеем:

z = exp(-²/2) (1-7.8)

Из (1-7.7) следует алгоритм получения чисел r(2n), распределенных по закону Релея:

p(2n) = {-2 ln[z(2n)]}^1/2 (1-7.9)

На рис. 1-7.5 в виде графика показано такого рода нелинейное преобразование случайных чисел z с равномерным распределением значений в пределах от 0 до 1, в результате которого получено релеевское распределение плотности вероятности модуля вектора r.

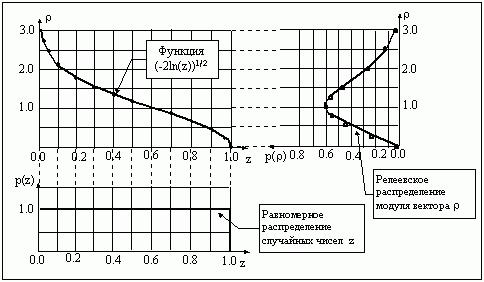
Рис. 1-7.5

Зная модуль r(2n) и фазу j(2n-1) 2n-го случайного вектора можно определить распределенные нормально проекции этого вектора на оси декартовой системы координат:

x_o(2n) = p(2n)cos(2n-1)

y_o(2n-1) = p(2n)sin(2n-1) (1-7.10)

Для формирования дельта-кррелированного нормированного и центрированного нормально распределенного процесса используются поочередно как числа xo(2n) так и числа yo(2n-1). Таким образом, каждому случайному числу z(n) с равномерным распределением будет соответствовать одна выборка u(n) дельта-коррелированного нормального процесса.

Н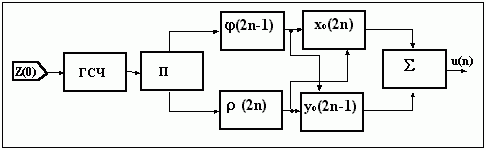 а рис. 1-7.6 представлена блок-схема программы для получения дельта-коррелированного нормированного и центрированного нормального процесса.

Рис. 1-7.6

На рисунке обозначено:

Z(0) - начальное случайное число;

ГСЧ - генератор случайных чисел с равномерным законом распределения;

П - переключатель случайных чисел с нечетными и четными номерами;

S - формирователь общего дельта-коррелированного (нормированного и центрированного) нормального процесса u(n) из двух однородных процессов x_o(2n) и y_o(2n-1).

Оценка математического ожидания МО* случайного процесса S(t) производится по алгоритму [10]:

(1-7.11)

а оценка дисперсии D*, соответственно, по формуле:

(1-7.12)

ХОД РАБОТЫ:

1. Исходные данные:

Количество выборок (N) = 100

Число для запуска ГСЧ (X_o) = 1

Математическое ожидание (МО) = 0.5

Среднеквадратическое отклонение (СКО) = 0.5

Время корреляции (T_к) = 10

Интервал между отсчетами (dt) = 1

Коэффициент корреляции (R) = 0.90484