
Лекции по молекулярной физике / Лекция 5
.doc3.5 Распределение Максвелла
Существуют и
другие распределения, используемые в
физике, кроме рассмотренных выше.
Распределение большого числа молекул
идеального газа (не квантовых частиц),
находящегося в состоянии термодинамического
равновесия, по модулям скоростей
подчиняется закону распределения
Максвелла.
Для получения дифференциального
распределения Максвелла (см.[1,2]) будем
искать число частиц, скорости которых
лежат в очень малом интервале d![]() вблизи
некоторой скорости
вблизи
некоторой скорости
![]() Пусть
dn
– число частиц в единице объёма, скорости
которых лежат в интервале от
Пусть
dn
– число частиц в единице объёма, скорости
которых лежат в интервале от
![]() до
до
![]()
d
d![]() Это
число пропорционально интервалу
скоростей d
Это
число пропорционально интервалу
скоростей d![]() ,
а также пропорционально числу частиц
в единице объёма. Можно записать так:
,
а также пропорционально числу частиц
в единице объёма. Можно записать так:
![]() ,
(3.18)
,
(3.18)
где
![]() -
плотность вероятности скорости, которая
означает долю частиц в единице объёма,
скорости которых лежат в единичном
интервале скоростей вблизи скорости
-
плотность вероятности скорости, которая
означает долю частиц в единице объёма,
скорости которых лежат в единичном
интервале скоростей вблизи скорости![]()
Тогда доля частиц, скорости которых
лежат в интервале от
Тогда доля частиц, скорости которых
лежат в интервале от
![]() до
до
![]()
d
d![]() может
быть найдена как
может
быть найдена как
![]() (3.19)
(3.19)
Поскольку число
частиц, даже в малых объёмах вещества,
очень велико, то
![]() имеет смысл вероятности того, что любая
частица идеального газа в единице объёма
имеет скорость, лежащую в интервале
скоростей от
имеет смысл вероятности того, что любая
частица идеального газа в единице объёма
имеет скорость, лежащую в интервале
скоростей от
![]() до
до![]()
d
d![]() Распределение
Максвелла в дифференциальной форме,
как показано в [1-3], имеет вид:
Распределение
Максвелла в дифференциальной форме,
как показано в [1-3], имеет вид:
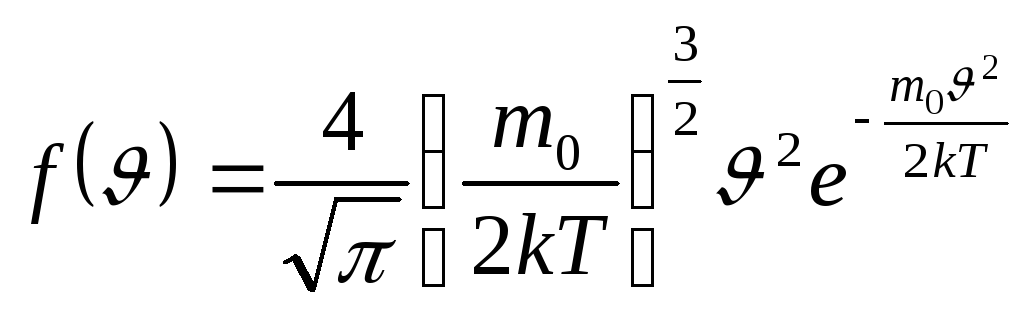 (3.20)
(3.20)
Вид дифференциального
распределения Максвелла при разных
значениях температуры представлен на
рисунке 3.10. Площадь заштрихованной
криволинейной трапеции на рис.3.10 численно
равна доле частиц, скорости которых
лежат в интервале от
![]() до
до
![]()
d
d![]() Скорость
Скорость
![]() ,
соответствующая максимуму плотности
вероятности
,
соответствующая максимуму плотности
вероятности
![]() ,
называется наиболее
вероятной скоростью.
При
,
называется наиболее
вероятной скоростью.
При
![]() выполняется равенство
выполняется равенство
![]() .
Отсюда получаем, что наиболее вероятная
скорость равна:
.
Отсюда получаем, что наиболее вероятная
скорость равна:
![]() или
или
![]() (3.21)
(3.21)

В отличие от
распределения Гаусса, распределение
Максвелла не симметрично относительно
абсциссы максимума функции распределения.
Это обусловлено наличием в формуле
(3.20) квадрата модуля скорости, кроме
экспоненты. При малых скоростях
![]()
![]() преобладает вклад
преобладает вклад
![]() ,
поэтому при этих скоростях вид кривой
дифференциального распределения
(рис.3.10) близок к параболе, при
,
поэтому при этих скоростях вид кривой
дифференциального распределения
(рис.3.10) близок к параболе, при
![]() основной
вклад вносит экспонента, которая убывает
гораздо быстрее, чем растёт парабола.
Площадь фигуры под кривой (
основной
вклад вносит экспонента, которая убывает
гораздо быстрее, чем растёт парабола.
Площадь фигуры под кривой (![]() )
на рис.3.10 равна единице (условие
нормировки) и выражает факт существования
молекулы. При возрастании температуры
увеличивается наиболее вероятная
скорость, а плотность вероятности,
соответствующая этой скорости,
уменьшается, но площадь фигуры под
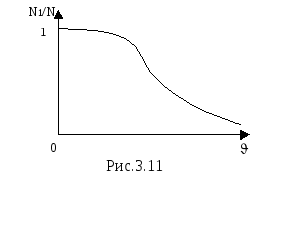
кривой остаётся неизменной. Интегральное
распределение Максвелла показано на
рисунке 3.11. Здесь N1/N
– доля частиц, скорости которых превышают
скорость
)
на рис.3.10 равна единице (условие
нормировки) и выражает факт существования
молекулы. При возрастании температуры
увеличивается наиболее вероятная
скорость, а плотность вероятности,
соответствующая этой скорости,
уменьшается, но площадь фигуры под
кривой остаётся неизменной. Интегральное
распределение Максвелла показано на
рисунке 3.11. Здесь N1/N
– доля частиц, скорости которых превышают
скорость![]() .
.
Таким образом, распределение Максвелла – это равновесное распределение идеального газа. Оно устанавливается благодаря столкновениям молекул, которые приводят систему к тепловому равновесию.
3.6. Распределение Максвелла для относительных (приведённых) скоростей
Для решения задач
удобно использовать формулу Максвелла
в форме, где скорости молекул выражены
в относительных единицах, приняв за
единицу скорости наивероятнейшую
скорость молекул. Обозначим относительную
(или приведённую) скорость через
![]() .
Распределение Максвелла в дифференциальной
форме будет иметь вид:
.
Распределение Максвелла в дифференциальной
форме будет иметь вид:
![]()
![]() ,
или
,
или![]() ,
здесь
,
здесь
![]() ,
а
,
а
![]()
![]() .
Графическое изображение f(U)
приведено
на рисунке 3.12. Для быстрого определения
f(U)
можно использовать таблицы, приведённые,
например, в [1] .
.
Графическое изображение f(U)
приведено
на рисунке 3.12. Для быстрого определения
f(U)
можно использовать таблицы, приведённые,
например, в [1] .
П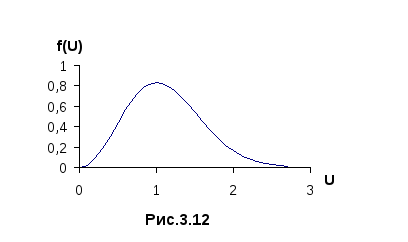 ри
решении задач на распределение Максвелла
необходимо сначала определить интервал
скоростей
ри
решении задач на распределение Максвелла
необходимо сначала определить интервал
скоростей
![]() и сравнить его со скоростями U1
и U2
- границами интервала. Если интервал
скоростей мал по сравнению со скоростями,
можно использовать дифференциальное
распределение Максвелла. Если интервал
скоростей велик, то нужно использовать
интегральное
распределение Максвелла.
Предположим, что нужно найти долю
молекул, относительные скорости которых
лежат в большом интервале от U1
до
U2.
В этом случае, чтобы избежать излишних
математических трудностей, нужно найти
сначала долю частиц, скорости которых
превышают скорость U1
:
и сравнить его со скоростями U1
и U2
- границами интервала. Если интервал
скоростей мал по сравнению со скоростями,
можно использовать дифференциальное
распределение Максвелла. Если интервал
скоростей велик, то нужно использовать
интегральное
распределение Максвелла.
Предположим, что нужно найти долю
молекул, относительные скорости которых
лежат в большом интервале от U1
до
U2.
В этом случае, чтобы избежать излишних
математических трудностей, нужно найти
сначала долю частиц, скорости которых
превышают скорость U1
:
 .
.
Затем нужно найти
долю частиц, скорости которых превышают
скорость U2
:
![]() .
.
После этого можно
найти долю частиц, скорости которых
лежат в большом интервале от U1
до
U2:
![]() .
.
Для определения
доли частиц, скорости которых не
превышают, например, скорость U1,
необходимо учесть условие нормировки,
выражающее факт существования частицы:
![]() .
Тогда долю частиц, скорости которых не
превышают скорость
U1
, находим
как:
.
Тогда долю частиц, скорости которых не
превышают скорость
U1
, находим
как:
![]() .
.
3.7 Средние скорости молекул
Распределение Максвелла позволяет определить несколько средних скоростей: наиболее вероятную скорость, среднюю арифметическую скорость и среднюю квадратичную скорость.
Скорость
![]() ,
соответствующая максимуму плотности
вероятности
,
соответствующая максимуму плотности
вероятности
![]() ,
называют наиболее
вероятной скоростью.
Для идеального газа, находящегося в
состоянии термодинамического равновесия
при температуре Т, она определяется из
условия
,
называют наиболее
вероятной скоростью.
Для идеального газа, находящегося в
состоянии термодинамического равновесия
при температуре Т, она определяется из
условия
![]() и
равна
и
равна
![]() или
или
![]() .
.
Средняя
квадратичная скорость
определяется как квадратный корень из
среднего квадрата скорости
![]() и
связана со средней кинетической энергией
поступательного движения молекул. Чтобы
найти её с помощью распределения
Максвелла, нужно определить отношение
суммы квадратов скоростей молекул,
содержащихся в единице объёма, к числу
молекул в этом объёме:
и
связана со средней кинетической энергией
поступательного движения молекул. Чтобы
найти её с помощью распределения
Максвелла, нужно определить отношение
суммы квадратов скоростей молекул,
содержащихся в единице объёма, к числу
молекул в этом объёме:![]() .
.
Для идеального газа, находящегося в состоянии термодинамического равновесия при температуре Т, она равна
![]() или
или
![]() (3.22)
(3.22)
Среднюю
арифметическую скорость
![]() определяют как отношение суммы всех
скоростей всех молекул в единице объёма
к числу молекул в единице объёма:
определяют как отношение суммы всех
скоростей всех молекул в единице объёма
к числу молекул в единице объёма:![]()
![]() .
.
Для идеального газа, находящегося в состоянии термодинамического равновесия при температуре Т , она равна :
![]() .
. (3.23)
.
. (3.23)
Эти
скорости мало отличаются друг от друга
по своим численным значениям :
![]() .
.
Экспериментально равновесное распределение частиц по скоростям было обнаружено Штерном, Истерманом и Симпсоном в 1947 году. Описание экспериментов см. в [1-3].
