Вопрос 6. Дискретно-событийные системы и модели. Схема алгоритма моделирования стохастических дискретно-событийных систем.

Дискретно-событийное моделирование — это вид имитационного моделирования. В дискретно-событийном моделировании функционирование системы представляется как хронологическая последовательность событий. Событие происходит в определенный момент времени и знаменует собой изменение состояния системы.

Компоненты дискретно-событийного моделирования:

Часы. Основной компонент системы, синхронизирующий изменения системы, т.е. возникновение событий.

Список событий. Система моделирования поддерживает по крайней мере один список событий моделирования. Однопоточные системы моделирования, основанные на мгновенных событиях, имеют только одно текущее событие. В то время как многопоточные системы моделирования и системы моделирования, поддерживающие интервальные события, могут иметь несколько текущих событий. В обоих случаях имеются серьезные проблемы с синхронизацией между текущими событиями.

Генераторы случайных чисел. Дискретно-событийные модели делятся на детерминированные и стохастические, в зависимости от того, каким образом генерируются события и основные характеристики очередей: время наступления событий, длительность обслуживания, количество клиентов, поступающих в очередь в единицу времени. Стохастические дискретно-событийные модели отличаются от моделей Монте-Карло наличием часов.

Статистика. Основные данные, которые собираются в системах дискретно-событийного моделирования:

• Средняя занятость (доступность) ресурсов

• Среднее количество клиентов в очереди

• Среднее время ожидания в очереди

Условие завершения. Условием завершения могут выступать:

• Возникновение заданного события (например, достижение 10мин времени ожидания в очереди)

• Прохождение заданного числа циклов по часам системы моделирования

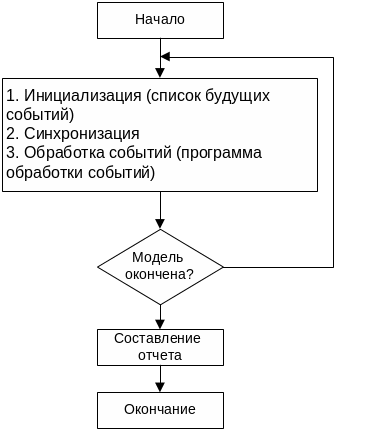
Схему моделирования дискретно-событийной системы можно представить в следующем виде: 1) Управляющий алгоритм циклически просматривает список событий S и находит очередное событие, которое должно быть реализовано в модели. В этом случае управляющий алгоритм вызывает специальный алгоритм (подпрограмму), с помощью которого выполняется или моделируется реализация события в системе. 

2) Алгоритмы обработки событий. Обычно рассматриваются события нескольких типов, причем действия, связанные в реализацией событий различных типов, могут отличаться друг от друга. 3) Помимо этого в схемы моделирования могут входить переменные и алгоритмы, предназначенные для сбора статистической информации.

Основной управляющий алгоритм имитационного моделирования стохастических дискретно-событийных систем.

Вопрос 7. Основные математические схемы моделирования систем и процессов (d,f,p,q – схемы).

при моделировании систем удобно пользоваться разработанными математическими схемами. Наиболее часто используются следующие схемы: непрерывно-детерминированные (D-схемы); дискретно-детерминированные (F-схемы); дискретно-стохастические (P-схемы); непрерывно-стохастические (Q-схемы).

К D-схемам относятся модели, описываемые системами дифференциальных уравнений или уравнений частных производных. В качестве независимой переменной, от которой зависит искомая функция, обычно служит время. Вектор–функция искомых переменных в этом случае является непрерывным.

Математическая схема такого вида отражает динамику изучаемой системы и поэтому называется D-схема (dynamic).

К F-схемам или дискретно-детерминированным моделям относится так называемый конечный автомат. Автомат можно представить, как некоторое устройство, на вход которого подаются входные сигналы и снимаются выходные сигналы и которое может иметь некоторое внутреннее состояние (память). У конечного автомата множество входных (выходных) сигналов и множество состояний являются конечными.

Автоматы широко используются в компиляторах, работают на допуск.

Конечные автоматы описываются 2-умя функциями:

Функции , задаются с помощью таблиц с двумя входами:

	Q1	Q2	…	Qm
A1
A2
…
An

Автомат задается в виде диаграмм перехода:

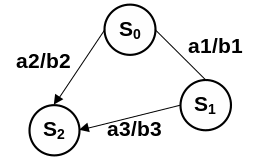
К P-схемам или дискретно-стохастическим моделям относятся вероятностные (стохастические) автоматы. Стохастические автоматы отличаются от обычных тем, что переход в новое состояние определяется не детерминировано, а с использованием вероятностной схемы, т.е. для каждого состояния и входного символа задается множество состояний, в которое автомат может перейти на данном такте в соответствии с заданным законом вероятности.

В общем виде вероятностный автомат можно определить как дискретный потактовый преобразователь информации с памятью, функционирование которого в каждом такте стохастически зависит от текущего входного символа и текущего состояния памяти.

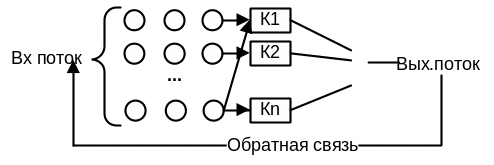
Q-схемы. Примером типовой схемы непрерывно-стохастического типа может служить система массового обслуживания.

В качестве процесса обслуживания в СМО могут быть представлены различные по физической природе процессы функционирования экономических, производственных и других систем.

В качестве входных потоков могут рассматриваться потоки товаров, клиентов, деталей и т.д. Для СМО характерно наличие следующих трех составляющих:

• Объектов, у которых возникает потребность в удовлетворении некоторых заявок, потребность в обслуживании.

• Агрегатов (каналов), предназначенных для удовлетворения заявок на обслуживание.

• Специальная организация приема заявок на обслуживание и их обслуживание.