6.3. Импульсные звенья

6.3.1. Квантование непрерывных сигналов. Процесс преобразования непрерывных функций в дискретные последовательности импульсов называется квантованием.

В цифровых САУ используется квантование по времени – это операция по преобразованию непрерывного сигнала в последовательность импульсов с фиксированным периодом дискретности. Квантование по времени достигается тем или иным видом модуляции: амплитудно-импульсная (АИМ) и широтно-импульсная (ШИМ).

При амплитудно-импульсной модуляции высота импульсов изменяется пропорционально значениям подаваемого на вход импульсного звена (ИЗ) непрерывного сигнала в дискретные, равностоящие моменты времени, как это показано на рис. 6.8, где – входная величина ИЗ (непрерывная); – выходная величина ИЗ (дискретная).

Период повторения Т и длительность импульсов остаются постоянными, следовательно, постоянна и скважность , представляющая собой отношение длительности импульса к периоду повторения .

В течение времени действия импульсов высота их может изменяться, либо оставаться постоянной.

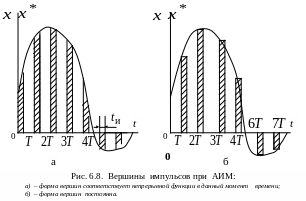
При широтно-импульсной модуляции высота импульсов остается постоянной, а их длительность или скважность находится в зависимости от значения непрерывной величины, подаваемой на вход ИЗ в моменты времени, равные периоду повторения, рис. 6.9. Большим значениям непрерывной функции соответствует меньшая скважность: если , то и .

САУ, в которых реализовано квантование по времени, называются импульсными САУ. Импульсные САУ с АИМ включают в себя класс цифровых САУ. В этих САУ амплитуда импульсов на выходе импульсного звена, фиксируемая через равностоящие промежутки времени, округляется до ближайшего большего или до ближайшего меньшего целого. САУ этого вида являются наиболее изученными и важными с точки зрения использования ЦВМ в контуре управления. При этом по теории Котельникова непрерывный сигнал с ограниченным частотным спектром в пределах от 0 до полностью определяется последовательностью своих дискретных значений, следующих через интервал прерывания (или частоту прерываний ).

6.3.2. Математическое описание импульсных звеньев и систем.

В общем случае импульсная САУ может быть представлена в виде сочетания импульсного звена (ИЗ) и непрерывной части (НЧ), чему соответствует схема на рис. 6.10. Форма вершин импульсов может быть самой разнообразной в зависимости от формы непрерывного сигнала.

Для облегчения задачи исследования импульсное звено представляют состоящим из двух частей: импульсного элемента (ИЭ), обеспечивающего на своем выходе сигнал в виде , и формирующего элемента (фэ), как это показано на рис. 6.11 а. Амплитуда импульсов при этом будет пропорциональна величине сигнала в момент замыкания ключа, рис. 6.11 б.

Формирующий элемент преобразовывает мгновенные импульсы на его входе в реальные импульсы следующим образом. Передаточная функция формирующего элемента подбирается таким образом, чтобы импульсная переходная характеристика ФЭ соответствовала форме непрерывного сигнала в течение времени, равного длительности реального импульса, рис. 6.11 б. Формирующий элемент реализуется путем подбора соответствующих типовых непрерывных звеньев, поэтому его также относят к непрерывной части системы. ФЭ и НЧ образуют приведенную непрерывную часть (ПНЧ) импульсной САУ.

Последовательность мгновенных, равноотстоящих импульсов на выходе ИЭ может быть представлена в виде дискретной функции (решетчатой функции), как это показано на рис. 6.12.

Дискретная функция определяется как числовая последовательность импульсов

(6.1)

Дискретная функция связана с непрерывной и, если интервал дискретности задан, может быть по ней определена однозначно:

при . (6.2)

Например:

; (6.3)

. (6.4)

Обратное утверждение несправедливо, так как одному значению дискретной функции может соответствовать множество различных непрерывных функций, рис. 6.12.

Если вместо указанной выше подстановки произвести подстановку , где – некоторая фиксированная величина в интервале времени от 0 до Т, то получим новую дискретную функцию , которая называется смещенной дискретной функцией.

Смещение может быть выражено в долях от интервала дискретности , где   1.

Тогда смещенная дискретная функция запишется так:

. (6.5)

При , смещенная функция превращается в несмещенную .

В дальнейшем несмещенную дискретную функцию будем обозначать , а смещенную – .

В отличие от непрерывных функций для исследования дискретных не существует производных и интегралов, однако есть их аналоги: конечные разности, конечные суммы и разностные уравнения.

Конечные разности – аналоги производных непрерывных функций – обозначаются символом  и определяются следующим образом.

Конечная разность первого порядка

Первая производная

(6.6)

Вторая производная

.

Пример. Дифференциальное управление первого порядка имеет вид:

Заменяя дифференциал конечной разностью первого порядка, полученной при такте квантования , имеем выражение

Конечная разность второго порядка

(6.7)

Конечная разность к- ого порядка определяется по формуле:

(6.8)

Рассмотрим определение конечных разностей для некоторых дискретных функций:

1. .

Первая разность (6.9)

Вторая и высшие разности равны нулю.

2.

Первая разность (6.10)

Конечные разности различных порядков характеризуют дискретную функцию в отдельных ее точках, рис. 6.13.

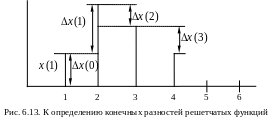
Конечные суммы – аналоги интегралов непрерывных функций. Определяются по формуле:

(6.11)

Уравнения в конечных разностях (разностные уравнения) – аналоги дифференциальных уравнений непрерывных функций – устанавливают соотношение между дискретной функцией и ее разностями. В общем случае линейное однородное разностное уравнение с постоянными коэффициентами может быть записано так:

(6.12)

где – искомая функция, – постоянные коэффициенты.

Учитывая связь конечных разностей с дискретами решетчатых функций, запишем уравнение следующим образом:

(6.13)

Рассмотрим это преобразование на примере уравнения 4-го порядка:

(6.14)

Определим конечные разности

(6.15)

Подставив значения конечных разностей в исходное уравнение и приведя подобные члены, получим:

(6.16)

Для решения разностных уравнений необходимо задание начальных условий в виде ординат искомой дискретной функции в точках .

Решение разностного уравнения, т.е. вид функции , позволяет судить об устойчивости импульсной САУ, которая описывается этим уравнением, и о некоторых показателях качества переходного процесса.

Однако непосредственное решение разностных уравнений представляет трудоемкий процесс, поэтому в теории импульсных систем разработаны методы, позволяющие оценить устойчивость и качество без решения разностного уравнения.

Для этой цели широко используется дискретное [D] и [Z] преобразования Лапласа.