Глава 3. Методы синтеза линейных сау

3.1. Коррекция сау

Под синтезом систем автоматического управления и регулирования понимается задача выбора и расчета параметров специальных корректирующих устройств, обеспечивающих заданные статические и динамические характеристики. При этом предполагается, что основные функциональные элемен­ты (исполнительные, усилительные и измерительные) уже выбраны и представляют собой неизменяемую часть CAP.

Особенностью CAУ корабельными техническими средствами является:

• четкое разделение системы на две части: объект регулирования и регулятор, причем инерционностью отдельных функциональных частей регулятора можно пренебречь по сравнению с инерционностью самого объекта регули­рования;

• использование типовых регуляторов. Поэтому общая задача синтеза для таких систем сводится к выбору типового регулятора, обеспечивающего требуемый закон ре­гулирования, и настройке его параметров в соответствии с динамическими характеристиками объекта.

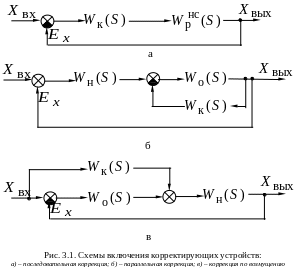
На рис. 3.1 показаны наиболее распространенные структурные схемы включения корректирующих устройств. При наиболее простой последовательной коррекции (рис.3.1 а) корректирующее устройство включается непосредственно в контур регулирования. Передаточная функция разомкнутой скорректированной CAP будет иметь вид:

(3.1)

где – передаточная функция разомкнутой нескорректированной системы;

– передаточная функция корректирующего устройства.

При параллельной схеме корректирующее устройство включается в цепь специальной обратной связи (рис. 3.1 б). Передаточная функция такой системы в разомкнутом виде

(3.2)

где – передаточная функция части CAP, охваченной корректирующей связью;

– передаточная функция части CAP, не охваченной корректирующей связью.

Формально всегда можно подобрать параллельную коррекцию так, чтобы получить тот же результат, что и при последовательной коррекции и наоборот.

В действительности выбор той или другой схемы коррекции зависит от особенностей технических и эксплуатационных характеристик применяемых функциональных элементов. Следует отметить, что применение параллельной коррекции повышает стабильность характеристик CAP. На третьей структурной схеме (рис. 3.1 в) показана коррекция по возмущению. Корректирующее устройство включается в дополнительную прямую связь, по которой измеряемое возмущение вводится в систему. По принципу действия такая коррекция существенно отличается от рассмотренных выше. Она не может влиять на свободные колебания и устойчивость замкнутой CAP; она улучшает качество CAP за счет уменьшения динамических ошибок по компенсируемому возмущению. В качестве корректирующих связей используются жесткие и гибкие связи. Жесткие связи описываются звеньями, имеющими статический коэффициент усиления. Они действуют постоянно. Гибкая связь действует только в переходном процессе и содержит дифференцирующее звено. Существуют, кроме того, интегрирующие связи, которые содержат в своей структуре интегрирующее звено. Рассмотрим влияние различных корректирующих связей на показатели устойчивости и качества CAP.

3.1.1. Гибкая параллельная корректирующая связь. Применяется для придания системе устойчивости и повышения её быстродействия. Место включения связи определяется конструктивными соображениями по наиболее простому формированию продифференцированного сигнала. Гибкая связь представляет собой дифференцирующее звено с передаточной функцией . Покажем влияние этого вида связи на примере CAP, cтpyктурная схема которой представлена на рис. 3.2.

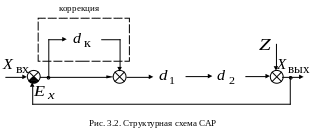
Пусть под действием приложенного возмущения Z в нескорректированной CAP произойдет переходный процесс с графиком ошибки регулирования , показанный на рис. 3.3 а. В этом случае регулирующее воздействие (см. выражение 1.24) M(t) равно самой ошибке регулирования .

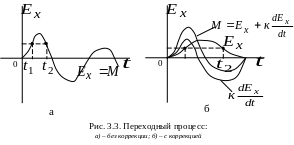
В моменты времени и ошибки и равны, но при ошибка возрастает, а при – убывает. CAP без коррекции на указанные особенности сигнала ошибки не реагирует. Вследствие этого переходный процесс получается длительным и имеет колебательный характер.

С целью улучшения качества регулирования надо иметь прямую зависимость регулирующего воздействия и величины ошибки : при возрастании – мощное воздействие, при убывании – слабое. Такой закон регулирования получается введением производной от ошибки. У скор­ректированной системы регулирующее воздействие выражается суммой двух слагаемых

Как видно из рис. 3.3 б, при равных значениях ошибки в моменты времени и регулирующие воздействия и будут различными. При убывающей ошибке принимает отрицательное значение. Это означает, что система осуществляет «одержание» объекта, создавая с помощью регулирующего органа силу, гасящую инер­цию объекта регулирования. Наличие производной в законе регулирования придает CAP свойство прогнозирования. Переходный процесс при этом оказывается не колебательным, а монотонным. Рассмотрим влияние гибкой корректирующей связи на устойчивость CAP с помощью критерия Найквиста. Пусть у нескорректированной CAP регулятор описывается апериодическим звеном 2-го порядка

а объект регулирования представлен апериодическим звеном

Передаточная функция разомкнутой CAP будет иметь вид

(3.3)

– коэффициент усиления CAP в разомкнутом состоянии.

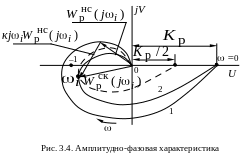
Выполнив замену S = j, получим комплексную передаточную функцию, по которой построим АФХ нескорректированной CAP. Амплитудно-фазовая характеристика показана на рис. 3.4, кривая 1.

Согласно критерию Найквиста CAP является неустойчивой, т.к. АФХ охватывает точку с координатами (–1, j0). Придать системе устойчивость можно за счет уменьшения коэффициента усиления регулятора , т.е. за счет уменьшения . При снижении в два раза точка (–1, j0) не будет охватываться AФX (пунктир на рис. 3.4), т.к. модули АФХ для всех  уменьшаются также в два раза. Проведем далее исследование, как это отразится на величине статической ошибки CAP.

Ошибка регулирования через передаточную функцию ошиб­ки будет

По теореме о конечном значении находим выражение стати­ческой ошибки

(3.4)

Уменьшение в два раза увеличивает статическую ошибку CAP почти в два раза. Это может нарушить требования системе по точности. Кроме того, уменьшение коэффициента снижает быстродействие CAP. Оценим влияние на устойчивость CAP гибкой связи при сохранении коэффициента усиления. Передаточная функция скорректированной системы будет иметь вид

Комплексная передаточная функция:

АФХ скорректированного контура получается путем сложения двух взаимно перпендикулярных векторов: – нескорректированная CAP и для каждого .

Из построения (рис. 3.4, кривая 2) видно, что введение в закон регулирования первой производной разворачивает АФХ скорректированной системы против часовой стрелки. При соответствующем подборе коэффициента дифференцирования CAP будет устойчивой. Оценим влияние гибкой связи на статическую погрешность. Имеем для скорректированной CAP

В установившемся режиме (при S = 0) ошибка определяется зависимостью (3.4). Это значит, что введение гибкой корректирующей связи улучшает условия устойчивости, но не влияет на величину статической погрешности.

3.1.2. Интегрирующая параллельная корректирующая связь. Введение в закон регулирования интегрирующего звена предназначается для придания CAP астатических свойств (уменьшение статической ошибки). Пусть корректирующая связь . Тогда передаточная функция скорректированной CAP в разомкнутом виде будет

Статическая ошибка в этом случае будет равна нулю

Введение в закон регулирования интеграла улучшает статическую точность CAP, но может привести к утрате устойчивости. Интегрирующее звено разворачивает АФХ по часовой стрелке. Это видно из выражения комплексной пе­редаточной функции

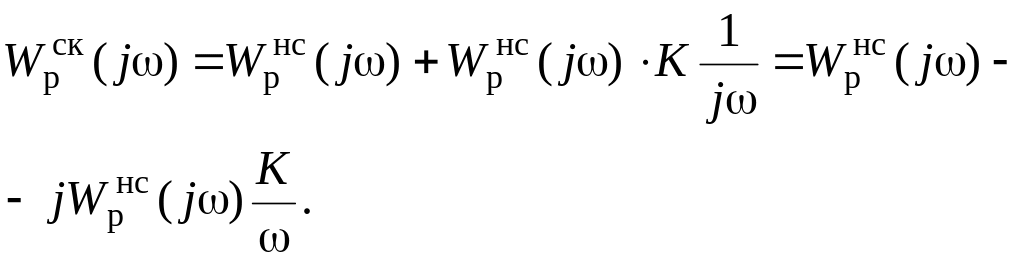
3.1.3. Корректирующие обратные связи. Для коррекции в CAP применяют главным образом отри­цательные обратные связи. Положительные обратные связи используют лишь для увеличения коэффициента усиления или уменьшения постоянной времени. Рассмотрим изменение ха­рактеристик ряда звеньев, охваченных различными обрат­ными связями.

1. Охват апериодического звена жесткой обратной связью (ЖОС)

С выхода апериодического звена снимается часть (-ая) сигнала и подается на его вход. Передаточная функция скорректированного звена будет иметь вид:

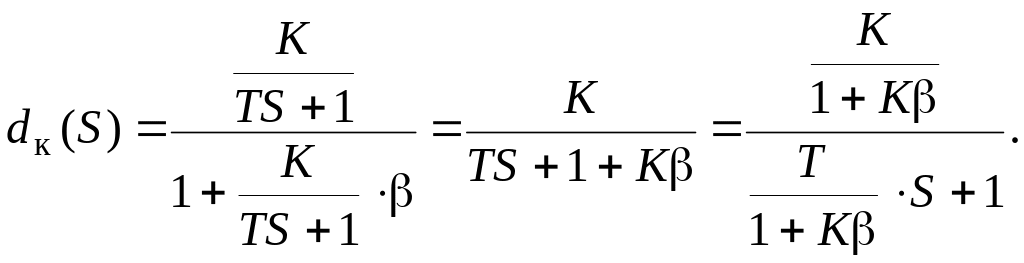(3.5)

Коэффициент передачи  цепи обратной связи определя­ет "жесткость" обратной связи или её глубину. С увеличением  обратная связь становится более глубокой, а при  = 1 сигнал с выхода (с отрицательным знаком) подает­ся на вход. Путем ввода ЖОС уменьшается постоянная време­ни Т звена в (1 +  K) раз.

Охват ЖОС позволяет уменьшить инерционные свойства зве­на, его запаздывание, а значит, повысить стабилизирующие свойства CAP. При этом наблюдается уменьшение коэффициента усиления, которое должно быть компенсировано за счет других звеньев CAP.

2. Охват интегрирующего звена ЖОС

В этом случае передаточная функция звена будет иметь вид:

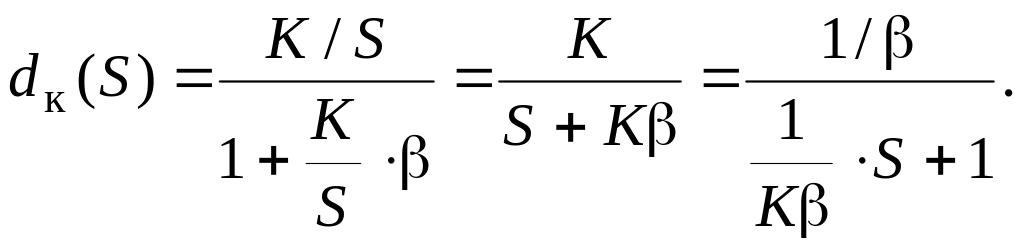(3.6)

Обозначим Т=1/К. Тогда получим из (3.6) переда­точную функцию апериодического звена, а при пренебрежимо малом Т – пропорциональное звено. Охват интегрирующего звена ЖОС уменьшает астатизм и запаздывающие свойства CAP.

Случаи 1 и 2 показывают, что применение ЖОС снижает коэффициент усиления звена. В некоторых случаях это снижение не может быть компенсировано за счет других элементов. Уменьшение коэффициента ведет к снижению точности и быстродействия CAP и является основным недостатком ЖОС.

3. Охват апериодического звена гибкой обратной связью (ГОС)

ГОС улучшает переходные характеристики звеньев, не уменьшая их статической точности. В качестве примера возьмем ГОС в виде изодромного звена с передаточной функцией

.

Тогда передаточная функция звена, охваченного изодромным звеном, будет иметь вид

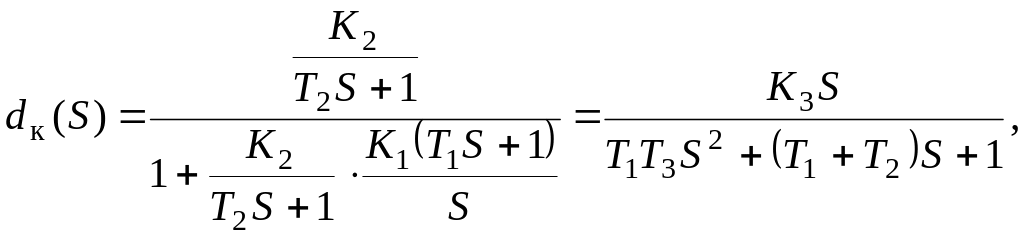(3.7)

где .

В результате охвата получено звено с дифференцирующими свойствами и изменившимся коэффициентом усиления.