Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

_____________________________________________________

И. А. Дроздова, Г. Б. Тодер

ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ

(ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ)

Утверждено редакционно-издательским советом университета

в качестве методических указаний для самостоятельной работы студентов

при решении задач по физике

Омск 2009

УДК 530.1(075.8)

ББК 22.3

Д75

Законы сохранения в механике (примеры решения задач): Методичес-кие указания к решению задач по физике / И. А. Дроздова, Г. Б. Тодер; Омский гос. ун-т путей сообщения. Омск, 2009. 38 с.

Приведены краткие теоретические сведения по теме «Законы сохранения в механике», примеры решения типовых задач на применение законов сохранения импульса, момента импульса и энергии в механике материальной точки и абсолютно твердого тела, которые должны уметь решать студенты согласно требованиям учебной программы.

Предназначены для студентов первого курса технических вузов дневной и заочной форм обучения.

Библиогр.: 6 назв. Табл. 1. Рис. 14.

Рецензенты: доктор техн. наук, профессор В. А. Нехаев;

канд. физ.-мат. наук, старший преподаватель А. А. Печерицын.

__________________________

© Омский гос. университет

п утей сообщения, 2009

Оглавление

Введение 1 1 5

1. Краткие теоретические сведения 11 6

2. Примеры решения задач 1 11

2.1. Работа. Энергия. Закон сохранения энергии 1 11

2.2. Закон сохранения импульса 1 15

2.3. Закон сохранения момента импульса 29

Библиографический список 1 38

Введение

При изучении курса физики решение задач имеет большое значение, поз-воляет лучше понять и запомнить основные законы физики, развивает навыки в применении теоретических знаний для решения конкретных практических воп-росов.

Цель настоящих методических указаний – оказать помощь студентам в освоении методики решения типовых задач по теме «Законы сохранения в механике».

Такие величины, как работа, энергия, импульс, момент импульса, и соот-ветствующие законы сохранения в механике играют важную роль в физике, так как связаны с симметриями пространства – времени. В задачах, решения которых представлены в данном издании, эти величины определяются, а законы применяются при вычислениях в рамках механики материальной точки и абсолютно твердого тела. Краткие теоретические сведения, необходимые для решения задач, приведены в настоящих указаниях, а теоретические сведения в полном объеме содержатся в книгах [1 – 6].

При решении задач с применением законов сохранения рекомендуется следующий порядок действий: 1) определить, какие состояния механической системы необходимо рассмотреть в данной задаче, и для каждого состояния сделать рисунок; 2) определить, какие законы сохранения являются существенными при переходе системы из одного состояния в другое по условиям задачи, и записать эти законы; 3) решить полученную систему уравнений, используя данные задачи.

Все задачи следует (по возможности) решать в общем виде. Это означает, что сначала выводится формула для расчета искомой величины, а затем в нее подставляются численные данные. Такой подход позволяет при анализе полученных формул увидеть общие закономерности. Прежде чем приступить к решению, следует внимательно прочитать, обдумать и записать условия задачи, перевести единицы измерения всех величин в основные единицы СИ, сделать схематический рисунок, отражающий условия задачи, выбрать подходящую систему отсчета. При вычислениях рекомендуется применять формулы приб-лижения, позволяющие упростить расчеты.

1. Краткие теоретические сведения

Для решения задач механики важнейшими характеристиками движения механических систем являются кинетическая энергия импульс момент импульса (момент количества движения, кинетический момент) а мерами действия силы – импульс силы работа и момент силы

Материальная точка массой движущаяся относительно инерциальной системы отсчета со скоростью имеет кинетическую энергию

, (1.1)

импульс момент количества движения где – радиус-вектор точки.

Полная механическая энергия системы равна алгебраической сумме механических энергий материальных точек, входящих в нее:

(1.2)

Полный импульс системы равен векторной сумме импульсов материальных точек, входящих в нее:

(1.3)

Полный момент количества движения системы равен векторной сумме моментов импульса материальных точек, входящих в нее:

, (1.4)

Абсолютно твердое тело, вращающееся вокруг неподвижной оси с угловой скоростью имеет кинетическую энергию

(1.5)

и момент импульса относительно оси вращения

(1.6)

где и – момент инерции тела относительно оси и проекция угловой скорости тела на ось соответственно.

Моменты инерции I_C однородных тел правильной геометрической формы массой m относительно оси, проходящей через центр масс, определяются по формулам, указанным в таблице.

Формулы моментов инерции I_C однородных тел правильной геометрической формы массой m относительно оси, проходящей через центр масс

Тело	Ось	Формула
Материальная точка массой m	Проходит на расстоянии R от точки	I = mR2
Тонкий однородный стержень длиной l	Перпендикулярна к стержню и проходит через его центр
Тонкий однородный стержень длиной l	Совпадает со стержнем
Шар радиусом R	Проходит через центр шара
Диск (цилиндр) радиусом R	Перпендикулярна к плоскости диска (основаниям цилиндра) и проходит через его центр
Кольцо (обруч) радиусом R	Перпендикулярна к плоскости кольца (обруча) и проходит через его центр	IC = mR2

Если ось не проходит через центр масс, то момент инерции тела относительно этой оси определяется по теореме Гюйгенса-Штейнера:

I_z = I_C + mb², (1.7)

где I_C – момент инерции тела относительно оси, параллельной оси и проходящей через его центр масс;

b – расстояние между осями.

Простейшим случаем движения абсолютно твердого тела, ось вращения которого не закреплена, является плоское движение, т. е. движение, при котором все точки тела движутся параллельно одной заданной неподвижной плоскости. Примером плоского движения может служить качение симметричного (относительно оси вращения) тела (например, цилиндра).

Плоское движение абсолютно твердого тела можно разложить на два составляющих движения: поступательное и вращательное относительно мгновенной оси (например, относительно мгновенной оси, проходящей через центр масс тела). Угловая скорость вращательного движения не зависит от выбора точки, через которую проходит мгновенная ось вращения, и во всех случаях она имеет одинаковое значение. Скорость поступательного движения всех точек тела одинакова и равна скорости поступательного движения его центра масс. Кинетическая энергия движущегося поступательно со скоростью тела массой определяется по формуле (1.1). Кинетическая энергия абсолютно твердого тела (АТТ) складывается из кинетической энергии поступательного и вращательного движения относительно мгновенной оси:

, (1.8)

где – момент инерции тела относительно этой оси.

Механическая энергия системы равна сумме ее кинетической и потенциальной энергий: .

Потенциальная энергия тела характеризует его взаимодействие с другими телами и полями, она зависит от взаимного положения тел и их положения во внешнем поле [3]. В частности, в поле силы тяжести Земли, вблизи поверхности Земли потенциальная энергия тела массой , центр тяжести которого находится на высоте от некоторого произвольно выбранного начала отсчета, рассчитывается по уравнению

(1.9)

при условии, что у поверхности Земли потенциальная энергия тела принимается равной нулю, и зависимость ускорения свободно падающего тела вблизи поверхности Земли от высоты не учитывается.

Потенциальная энергия упруго деформированного вдоль некоторой оси OX тела жесткостью k (в поле силы упругости при малой линейной деформации)

(1.10)

при условии, что в недеформированном состоянии потенциальная энергия тела принимается равной нулю.

В общем случае работа , совершаемая силой при перемещении материальной точки из точки M₁ в точку M₂, определяется по формуле:

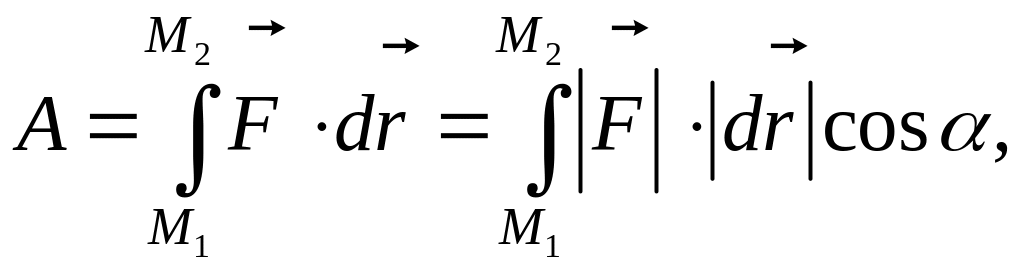(1.11)

где – скалярное произведение векторов силы и перемещения ;

– угол между этими векторами.

Из формулы (1.11) получаем выражение для работы, которая совершается силой, не зависящей от положения материальной точки:

. (1.12)

При движении материальной точки в поле консервативных сил это поле совершает работу, не зависящую от пути, по которому движется точка. При перемещении материальной точки из положения, определяемого радиусом-векто-ром , в положение, определяемое радиусом-вектором , работа консервативной силы равна убыли потенциальной энергии точки:

. (1.13)

Например,

; (1.14)

. (1.15)

При вращении абсолютно твердого тела вокруг неподвижной оси внешняя сила, создающая момент совершает работу:

, (1.16)

где – проекция вектора на направление угловой скорости.

Знак работы зависит от знака

Связь между характеристиками движения и мерами действия силы отражается в общих теоремах динамики [4, 6] об изменении импульса, момента импульса и кинетической энергии. Из этих теорем выводятся законы сохранения импульса, момента импульса и механической энергии соответственно. Эти законы описывают свойства движения и взаимодействия любой системы материальных точек.

Теорема об изменении кинетической энергии: изменение кинетической энергии системы при ее переходе из состояния 1 в состояние 2 происходит под действием сил, приложенных к точкам системы, и равно сумме работ этих сил при данном переходе:

(1.17)

С помощью теоремы об изменении кинетической энергии решаются многие задачи механики.

Сила называется диссипативной, если ее действие приводит к диссипации механической энергии – переходу механической энергии в тепловую. Все силы сопротивления движению (например, сила трения) являются диссипативными.

Закон сохранения механической энергии: при отсутствии диссипативных сил механическая энергия системы остается постоянной, она может переходить из кинетической энергии в потенциальную и обратно:

(1.18)

Сила называется консервативной, если ее работа по изменению состояния системы зависит только от начального и конечного состояния системы и не зависит от способа изменения состояния. Консервативные силы не являются диссипативными, поэтому закон сохранения механической энергии выполняется, если на систему и внутри нее действуют только консервативные силы.

При наличии диссипативных сил к системе применим общефизический закон сохранения энергии: энергия в природе ниоткуда не возникает, никуда не исчезает, а при любых взаимодействиях лишь переходит из одной формы в другую, от одного тела к другому.

Закон сохранения импульса: если результирующая внешних сил, действующих на систему, равна нулю, то полный импульс системы не меняется при любых взаимодействиях внутри системы:

(1.19)

Система называется замкнутой, если на нее не действуют внешние силы, поэтому в замкнутых системах закон сохранения импульса выполняется.

В случае, когда результирующая внешних сил не равна нулю, но ее проекция на некоторое направление обращается в нуль, остается постоянной проекция импульса системы на это направление.

Закон сохранения момента импульса: если результирующий момент внешних сил, действующих на систему, равен нулю, то полный момент импульса системы не меняется при любых взаимодействиях внутри системы:

(1.20)

Силы, направленные только к одной точке или от нее, называются цент-ральными, а эта точка – центром. Момент центральной силы равен нулю, поэтому для систем, на которые действуют только центральные силы, также как и для замкнутых систем, справедлив закон сохранения момента импульса.

В случае, когда результирующий момент внешних сил, действующих на систему, не равен нулю, но его проекция на некоторую ось (момент сил относительно оси) равна нулю, момент импульса системы относительно этой оси остается постоянным.

Благодаря применению законов сохранения оказывается возможным решение задач на взаимодействие тел в случаях, когда характер сил взаимодействия неизвестен. Однако прежде чем применять закон сохранения, необходимо убедиться в том, что рассматриваемая система является именно той, в которой данный закон выполняется. Следует обратить внимание также на то, что все характеристики, входящие в уравнения, составленные на основании законов сох-ранения, должны рассчитываться относительно одной и той же инерциальной системы отсчета.