2.5.3 Статистичні характеристики приведеної несучої здатності

При розрахунку надійності сталевих елементів конструкцій постійне навантаження вводиться як поправка до несучої здатності елемента. В результаті цього до розгляду залучається випадкова величина приведеної несучої здатності – для першого граничного стану, із наступними статистичними характеристиками:

, (2.6)

, (2.7)

(2.8)

де – коефіцієнт впливу постійного навантаження.

1. Визначаємо коефіцієнт впливу постійного навантаження. Для даної розрахункової схеми (вільно оперта балка на двох опорах, що завантажена рівномірно розподіленим навантаженням), матимемо:

. (2.9)

Для трьох типів покрівлі коефіцієнт становить:

• Т1: 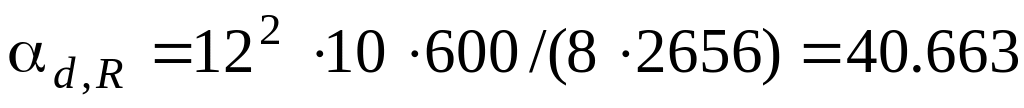МПа/кПа;

• Т2: 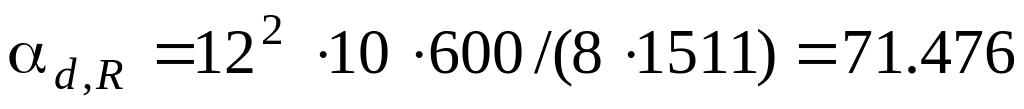МПа/кПа;

• Т3: 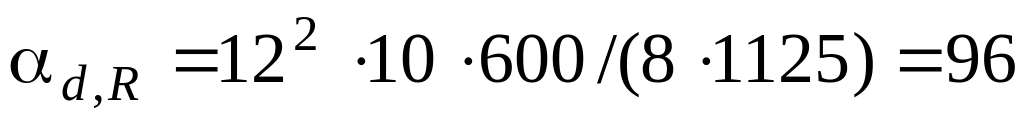МПа/кПа.

2. Визначаємо статистичні характеристики приведеної несучої здатності кроквяної балки. За формулами 2.6 – 2.8 маємо:

• Т1: 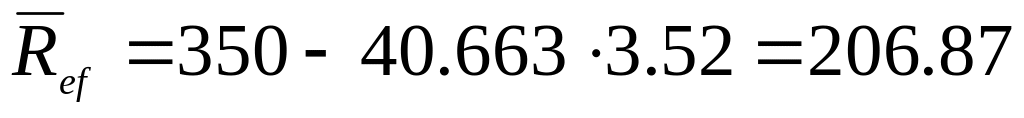МПа;

МПа;

.

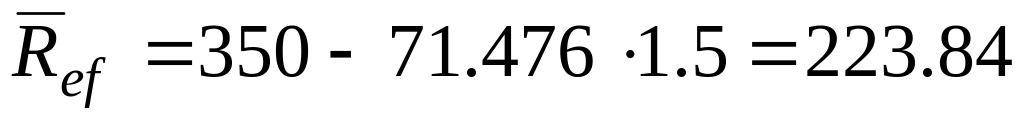• Т2: МПа;

МПа;

.

• Т3: 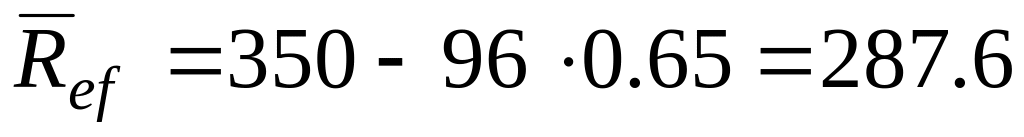МПа;

МПа;

.

2.5.4 Статистичні характеристики снігового навантаження

При розрахунках надійності сталевих елементів конструкцій снігове навантаження подається у формі квазістаціонарного диференційованого випадкового процесу , який однозначно визначається наступними параметрами:

1) нормованою щільністю розподілу ординати випадкового процесу;

2) математичним сподіванням ;

3) ефективною частотою ;

4) коефіцієнтом широкосмуговості ;

5) коефіцієнтом варіації ;

6) коефіцієнтом асиметрії .

Нормована щільність розподілу випадкового процесу снігового навантаження описується поліномо-експоненціальним законом [5, 7]:

, (2.10)

де – нормований ухил від центру розподілу ординати випадкового процесу; , – математичне сподівання і стандарт випадкового процесу снігового навантаження; – коефіцієнти поліномо-експоненціального закону, що є функціями асиметрії та коефіцієнта варіації випадкового процесу снігового навантаження. Параметри визначаються за методом моментів як рішення системи трансцендентних рівнянь:

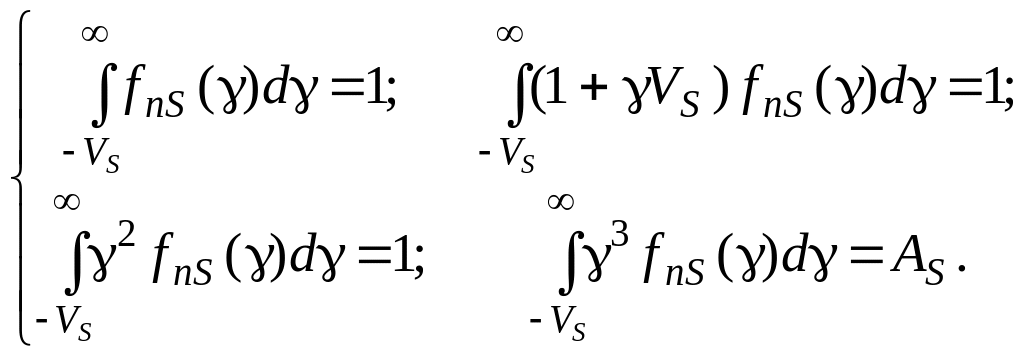(2.11)

1. Значення математичного сподівання, коефіцієнта варіації випадкового процесу снігового навантаження для різних регіонів України [4, 5] можуть визначатися за картами 3, 4 додатка А або табл.3 додатка Б.

Для м. Полтави кПа, .

Стандарт обчислимо за формулою: кПа.

2. Нормований характеристичний максимум та характеристична інтенсивність випадкового процесу снігового навантаження повинні визначатися у вигляді:

• нормований характеристичний максимум:

корінь рівняння: ; (2.12)

• характеристична інтенсивність:

, (2.13)

де – установлений термін експлуатації конструкції, який приймається за технічним завданням, а у випадку його відсутності може бути прийнятий за додатком В ДБН [3]; – коефіцієнт тривалості зимового періоду для території України [6]. Також дозволяється нормований характеристичний максимум і характеристичну інтенсивність випадкового процесу снігового навантаження визначати за асимптотичними формулами:

• нормований характеристичний максимум:

(2.14)

• характеристична інтенсивність:

, (2.15)

де та – безрозмірні коефіцієнти, що регламентуються таблицею 3 додатка Б.

Для м. Полтави з табл.3 додатка Б виписуємо значення коефіцієнтів та :

, , ,

, , .

За формулами (2.15) і (2.16) за заданим строком експлуатації кроквяної балки років визначаємо величини та :

,

.

3. Дальність розрахункового значення снігового навантаження є безрозмірною величиною і визначається як відношення розрахункового значення навантаження до його середнього значення , тобто

, (2.16)

.

4. Частка впливу снігового навантаження для першого граничного стану повинна знаходитися за формулою:

, (2.17)

де – коефіцієнт, що характеризує недонапруження або перенапруження елемента конструкції (значення відповідає випадку, коли елемент конструкції підібраний без запасу).

Визначаємо частку впливу снігового навантаження, враховуючи, що в цьому випадку коефіцієнт впливу снігового навантаження дорівнює коефіцієнта впливу постійного навантаження . У випадку, коли ця обставина не має місця, спочатку необхідно встановити значення коефіцієнта , подібно до того, як це робилось для постійного навантаження:

• Т1: ;

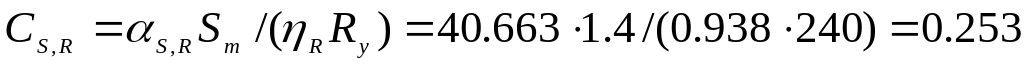• Т2: ;

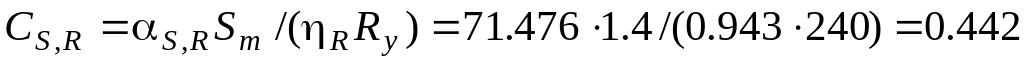• Т3: .

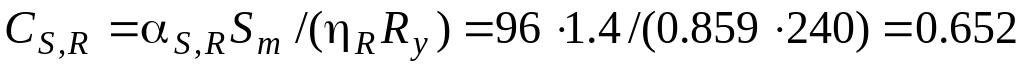5. Стандарт випадкового процесу напружень в елементі від дії снігового навантаження знаходимо за формулою:

. (2.18)

• Т1: 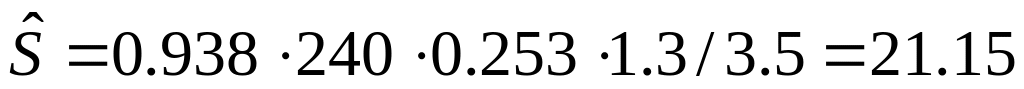МПа;

• Т2: МПа;

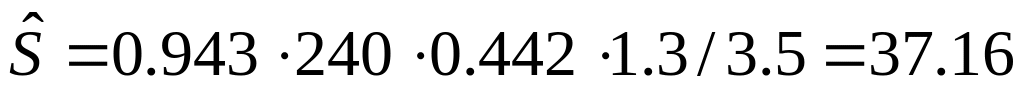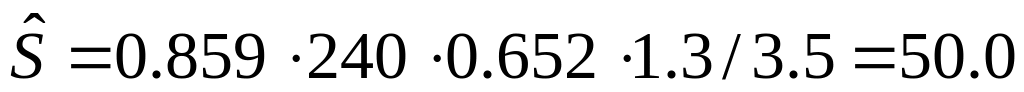• Т3: МПа.