В) Индуктивные сопротивления рассеяния обмоток.

 Определение потокосцеплений рассеяния, а следовательно, и индуктивных сопротивлений рассеяния х₁ и х₂ представляет собой сложную задачу, точное решение которой не представляется возможным. Поэтому при практических расчетах довольствуются приближенными методами, достаточная точность которых подтверждается опытом.

Индуктивное сопротивление может быть представлено в следующем виде:

.          (3-163)

Здесь угловая частота , а индуктивность рассеяния

.          (3-164)

где  — некоторая расчетная проводимость для индукционных трубок поля рассеяния. Из (3-163) и (3-164) получаем:

.          (3-165)

Индукционные линии поля рассеяния, например статора, условно делят на три группы; в соответствии с этим различают три вида рассеяния: пазовое, дифференциальное и лобовых частей обмотки. Если ввести коэффициенты проводимости — пазового рассеяния , дифференциального рассеяния , и рассеяния лобовых частей , отнесенные к единице длины статора или ротора l, то выражение (3-165) после ряда преобразований примет следующий вид, Ом:

,          (3-166)

где

.          (3-167)

Коэффициент проводимости пазового рассеяния  для диаметральных двухслойных обмоток (y = ) и для однослойных обмоток зависит только от геометрических размеров паза. Его определяют по потокосцеплению индукционных линий, проходящих поперек паза, с проводниками, лежащими в пазу (рис. 3-52).

Рис. 3-52. К определению .

При этом пренебрегают магнитным сопротивлением индукционных трубок пазового поля рассеяния вне паза и считают, что сопротивление для них определяется только расстояниями между стенками паза в той части, где лежат проводники, и в части паза над проводниками. Очевидно, что это сопротивление будет тем меньше, чем больше глубина паза (h₁ + h₂ + h₃ + h₄) и чем меньше его ширина b_п.

Для хордовых двухслойных обмоток (y < τ) коэффициент  зависит также и от значения , так как при < 1 в некоторых пазах находятся катушечные стороны, принадлежащие разным фазам (рис. 3-15), вследствие чего общее потокосцепление какой-либо катушечной стороны в этих пазах уменьшается. Следовательно, пазовое рассеяние при y < τ будет меньше, чем при y = τ.

Расчет  производится по формулам:

(для паза по рис. 3-52,а);

(для паза по рис. 3-52,б), где .

Для нормальных машин  = 0,8  2.

Коэффициент проводимости дифференциального рассеяния  в большой степени зависит от числа пазов q₁ (или q₂). шага обмотки. Рассматриваемое рассеяние определяется потокосцеплениями, которые создают высшие гармоники поля, например, статора с его обмоткой. Они наводят в обмотке э.д.с. той же частоты, что и 1-я гармоника поля (§ 3-4,б). Практически они зависят только от тока статора и от проводимости воздушного зазора. Просуммировав указанные э.д.с. и разделив полученную сумму на ток, мы найдем сопротивление х_д, соответствующее дифференциальному рассеянию (или высшим гармоникам поля). От х_д мы можем перейти к коэффициенту . Его значение  = 1  2,5. Оно тем меньше, чем больше число пазов q, длина воздушного зазора и чем ближе у к 0,83.

Для упрощения расчетов иногда составляют эмпирические формулы, рассматривая вместо дифференциального рассеяния поле рассеяния между соседними коронками (внешними поверхностями) зубцов. Индукционные трубки этого поля проходят через воздушные зазоры и частично через коронки зубцов противолежащей части машины. Их магнитная проводимость определяется в основном длиной воздушного зазора .

Коэффициент проводимости рассеяния лобовых частей обмотке  зависит от длины лобовой части. Его значение  = 0,6  1,5.

В относительных единицах измерения

; .          (3-168)

Для нормальных машин  о.е.

При больших скольжениях (s > 0,10), при которых обычно в обмотках имеют место большие токи, х₁ и х₂ несколько уменьшаются, так как уменьшаются  и х_д из-за насыщения тех стальных участков, по которым частично проходят индукционные трубки соответствующих полей рассеяния. Кроме того, х₂ уменьшается из-за неравномерного распределения тока по сечению стержней обмотки ротора, с чем приходится считаться при глубоких пазах и высоких стержнях (§ 3-19,в).

3-17. Круговая диаграмма

Круговая диаграмма асинхронной машины представляет собой геометрическое место концов вектора тока , изменяющегося при изменении скольжения s в пределах от + ∞ до -∞, если при этом напряжение на зажимах статора машины и все ее параметры сохраняют постоянные значения. Ее называют также диаграммой тока. Она дает наглядное представление о важных зависимостях между величинами, характеризующими работу асинхронной машины.

Обратимся к схеме замещения, представленной на рис. 3-49. Введем обозначение:

.          (3-169)

Тогда в соответствии со схемой замещения и уравнениями (3-120) и (3-121) можем написать:

.          (3-170)

Комплексный коэффициент C₁ согласно (3-126) равен:

,          (3-171)

где

          (3-172)

и

.          (3-173)

Подставив в (3-170) значение C₁ по (3-171), будем иметь:

что после преобразований дает:

,          (3-174)

где

;          (3-175)

.          (3-176)

Разделив (3-174) на , получим:

.          (3-177)

Три вектора полученного уравнения токов образуют при токе , соответствующем некоторому скольжению s, прямоугольный треугольник A_cAD, представленный на рис. 3-53, где вектор  направлен по вертикали. В этом треугольнике катеты  и , и гипотенуза  (в соответствии с обычными соотношениями между параметрами асинхронной машины принято, что угол γ₁ имеет отрицательное значение).

Рис. 3-53. Круговая диаграмма асинхронной машины.

При  отрезок . Поэтому конец вектора  (вершина прямого угла А) при изменении скольжения s опишет окружность, имеющую диаметр

.          (3-178)

Прибавив к вектору  постоянный вектор  получим вектор первичного тока . Отсюда следует, что конец вектора тока  при изменении s будет скользить по той же окружности, что и вектор .

Отложим в произвольном масштабе ; тогда в том же масштабе , так как треугольник сопротивлений A_cBR и треугольник токов A_cAD подобны. Отрезок A_cR в масштабе сопротивлений, очевидно, равен . Теперь разделим отрезок  на части:

;

;

.

При уменьшении s точка R. будет скользить вверх по прямой EF; соответствующая точка А будет скользить по окружности влево.

При s = 0 точка R уходит в бесконечность, точка А совпадает с точкой A_с, и мы получаем ток синхронизма .

При увеличении s точка R смещается вниз и точка А скользит вправо; при s = l точка R совпадает с точкой R_к, а точка А — с точкой А_к. Режим работы асинхронной машины при s = 1 по аналогии с трансформатором называется режимом короткого замыкания. Ток  (не показан на рис. 3-5З) — ток короткого замыкания.

Дуга А_cАА_к соответствует работе машины двигателем, так как по ней будет скользить ток  при изменении s от 0 до 1. При дальнейшем увеличении s от 1 до + ∞ точка R перемещается вниз, точка А — вправо и при s = + ∞ точка R попадает в точку R_∞, а точка А — в точку А_∞. Малая дуга А_кА_∞ соответствует изменению s от 1 до + ∞ и, следовательно, работе машины тормозом.

При s = -∞ точка R также совпадает с точкой R_∞, а точка А — с точкой A_∞. При отрицательном s и при его уменьшении по абсолютной величине точка R скользит вниз от R_∞, а точка А — вниз от A_∞. При s = 0, как отмечалось, точка А совпадает с точкой A_с. Дуга A_∞EA_c с соответствует изменению s от - ∞ до 0 и, следовательно, работе машины генератором.

Полученная диаграмма позволяет найти для любого тока I₁ соответствующий ему cosφ₁. Из диаграммы мы можем также получить ряд других величин, характеризующих работу машины.

Проведем через точку А перпендикулярно оси абсцисс отрезок . Пусть при построении круговой диаграммы был выбран масштаб для тока С_I , A/мм. Тогда ; где  измеряется в миллиметрах. Умножив полученный активный ток статора на число фаз m₁ и напряжение U₁, получим электрическую мощность статора:

,          (3-179)

где масштаб для мощности, Вт/мм,

.          (3-180)

Таким образом, перпендикуляр из любой точки диаграммы тока на ось абсцисс, измеренный в масштабе мощности, равен электрической мощности статора. Поэтому ось абсцисс называется линией электрических мощностей P₁.

Из подобия треугольников A_cRR_к и А_сАP'₂ следует:

.

Умножив обе части равенства на масштаб мощности, получим:

или

           ,          (3-181)

так как

 и .

Следовательно, линия A_cA_∞ —линия механических мощностей , развиваемых ротором.

Аналогично из подобия треугольников A_сRR_∞ и A_сAР_эм следует:

.          (3-182)

Следовательно, линия А_cА_∞ — линия электромагнитных мощностей Р_эм; в то же время это есть линия электромагнитных вращающих моментов М, так как М равен мощности Р_эм, деленной на синхронную угловую частоту , Дж,

          (3-183)

или, кг·м,

,

где масштаб для момента., кг·м/мм,

.          (3-184)

Отрезок , измеренный в масштабе мощности, равен электрическим потерям в обмотке ротора:

.          (3-185)

Согласно (3-69) скольжение

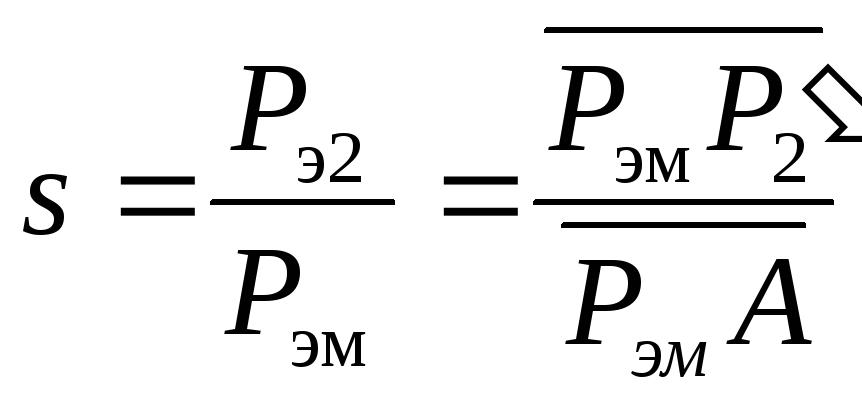.          (3-186)

При небольших токах I₁ (например, при I₁ < ) достаточно точное определение s по (3-186) затруднительно, поэтому для определения s применяют особое построение на диаграмме, рассмотренное в § 3-18,б.

При помощи диаграммы можно определить максимальный момент М_м. Для этого нужно параллельно линии моментов А_сА_∞ провести касательную к окружности и из точки касания А_м — перпендикуляр к диаметру  до пересечения с линией А_cА_∞, тогда получим, кг·м,

.

Обычно асинхронные двигатели рассчитываются таким образом, чтобы cosφ_н при номинальной нагрузке был равен максимальному (или близок к максимальному). В этом случае ток статора  будет совпадать с касательной к окружности (или будет близок к ней). Номинальный момент М_н = . Кратность максимального момента (способность к перегрузке)

.

Методы построения круговой диаграммы по расчетным или опытным данным и определение с ее помощью рабочих кривых двигателя, характеризующих его рабочие свойства, рассматриваются в § 3-18,б.

При построении рассмотренной круговой диаграммы было принято, что параметры асинхронной машины r₁, , x₁, , r₁₂, x₁₂ остаются без изменения, а изменяется только скольжение s. Никаких других допущений не делалось. Поэтому представленная на рис. 3-53 диаграмма называется точной круговой диаграммой.

Для обычных случаев, как отмечалось, комплекс С₁ можно заменить его модулем с₁ и принять, следовательно, γ₁ = 0. Тогда построение круговой диаграммы упрощается: ее диаметр расположится на линии, параллельной оси абсцисс; отрезки прямых, определяющие мощности и вращающие моменты, будут перпендикулярны к оси абсцисс. Такая упрощенная круговая диаграмма и используется при исследовании асинхронных машин, если угол γ₁ не превышает примерно 2  3°.

На практике к точной круговой диаграмме приходится обращаться при исследовании: малых машин, имеющих относительно высокое значение r₁; машин, работающих при низкой частоте тока [когда индуктивные сопротивления уменьшаются, а активные сопротивления практически остаются неизменными, что приводит согласно (3-173) к возрастанию γ₁];

машин, работающих с большим активным сопротивлением, включенным последовательно с обмоткой статора.

3-18. Рабочие характеристики двигателей