4. Рівняння гіперболічного типу

4.1 Рівняння коливань струни

Розглянемо задачу, що приводить до рівняння гіперболічного типу. Нехай маємо струну, у вигляді тонкої гнучкої нитки, жорстко закріпленої з двох кінців. Якщо її відхилити від положення рівноваги та відпустити, то вона почне виконувати поперечні коливання. Позначимо відхилення точок струни від положення рівноваги відносно осі через . Звісно, що є функція координати та часу (рис.4.1).

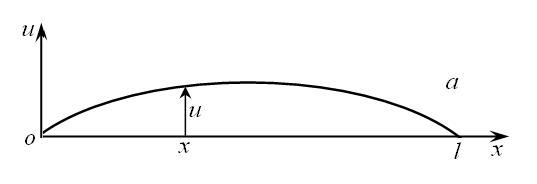
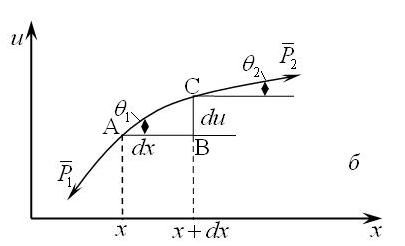
Рисунок 4.1

Задача полягає у знаходженні положення точок струни у будь-який момент часу , а саме – у визначенні функції .

Побудуємо математичну модель процесу коливання струни.

Розглянемо нескінченно малий елемент дуги струни . Замінивши його відрізком прямої із можемо записати . Виконавши граничний перехід та перейшовши до диференціалів, будемо мати

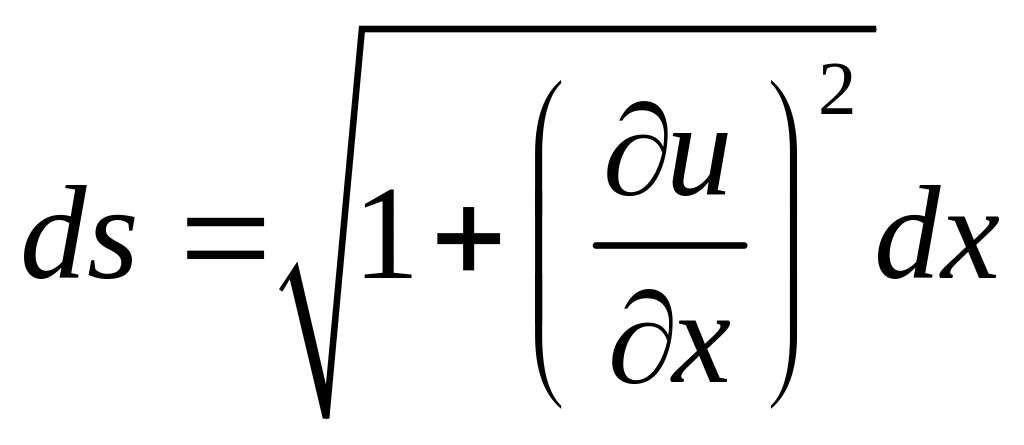(4.1) Якщо то ним, під знаком радикала, можна знехтувати. Тому у першому наближенні можемо записати, що .

Для нерозтяжної струни будемо вважати, що її натяг незмінний за величиною. Застосувавши до елемента струни другий закон Ньютона, ( ) та узявши ( - щільність струни), - прискорення, можемо записати

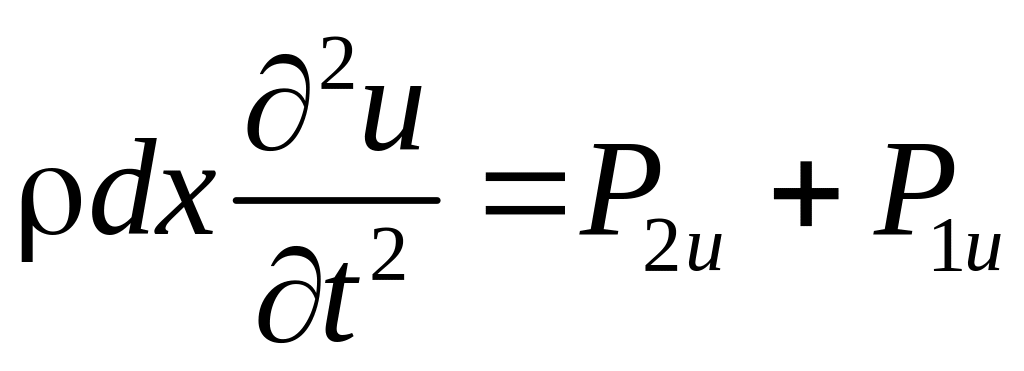, (4.2)

де – проекції векторів та на вісь (Рис.4.1).

Рівняння (4.2) називається рівнянням руху точок струни.

Нехай сили натягу діють з обох боків елемента . Хоча натяг на струні всюди сталий за модулем , у відхиленій струні натяг змінюється за напрямком. З рисунка видно, що проекції векторів та на вісь мають різні знаки .

Для малих кутів можемо записати, що

Підставивши отримані значення до правих частини рівняння (4.2) та урахувавши, що знаки та протилежні отримаємо

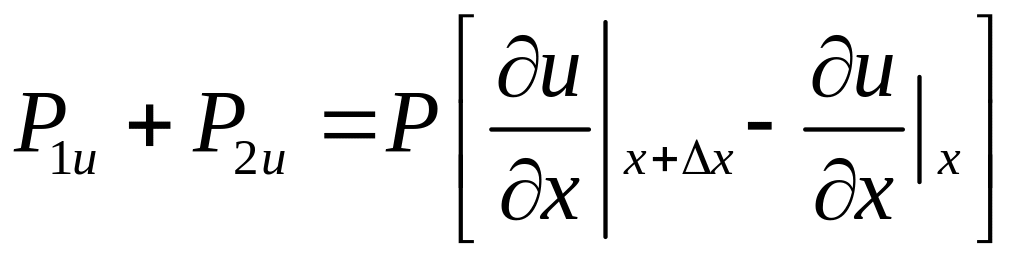
Перейшовши до границі, будемо мати

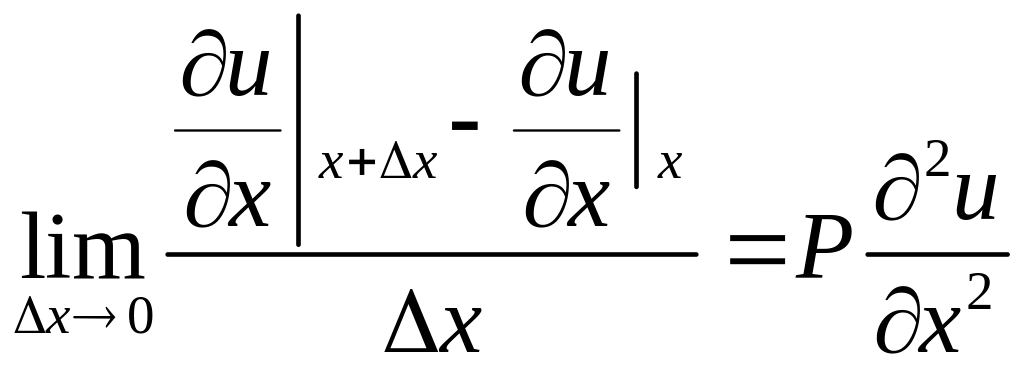(4.3)

З іншого боку, розклавши 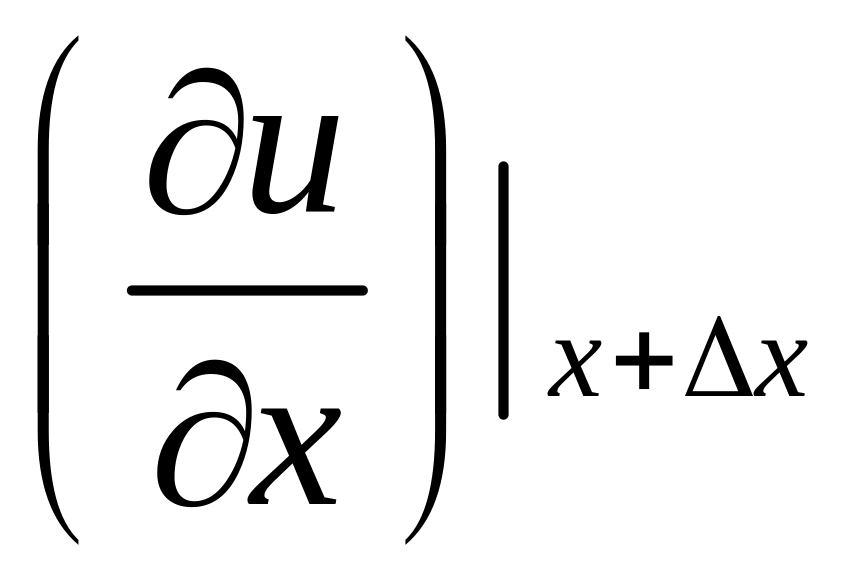у ряд Тейлора , будемо мати

.

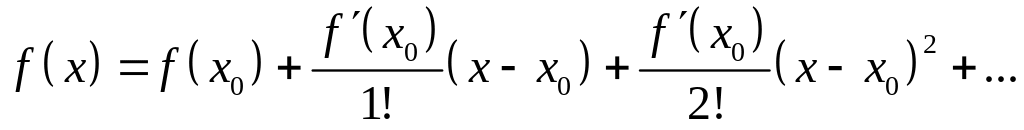
З точністю до нескінченно малих другого порядку, можемо записати

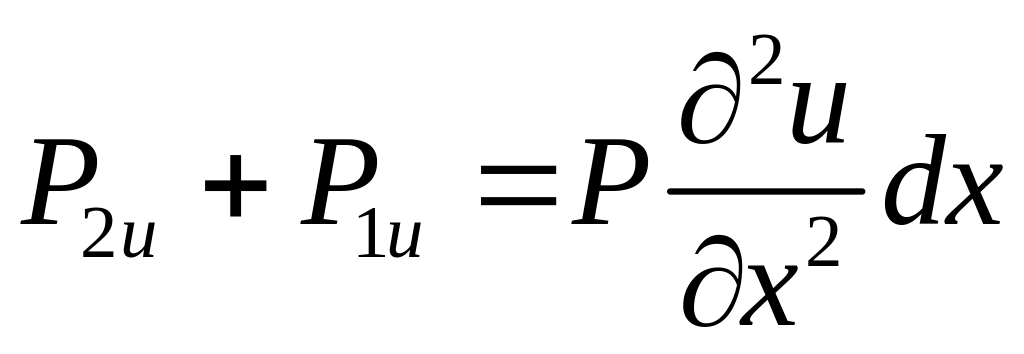
Підставивши (4.3) у (4.2), отримаємо одномірне рівняння коливань струни у вигляді

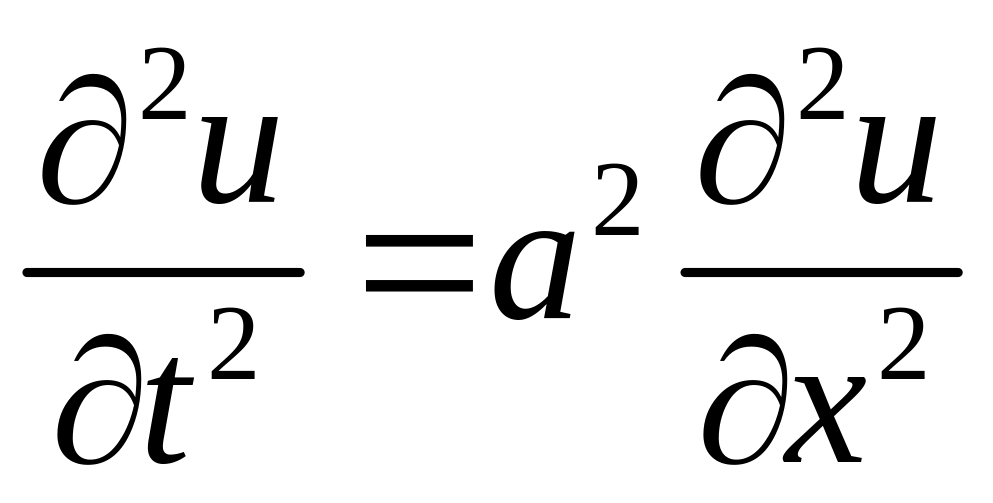, (4.4)

де .

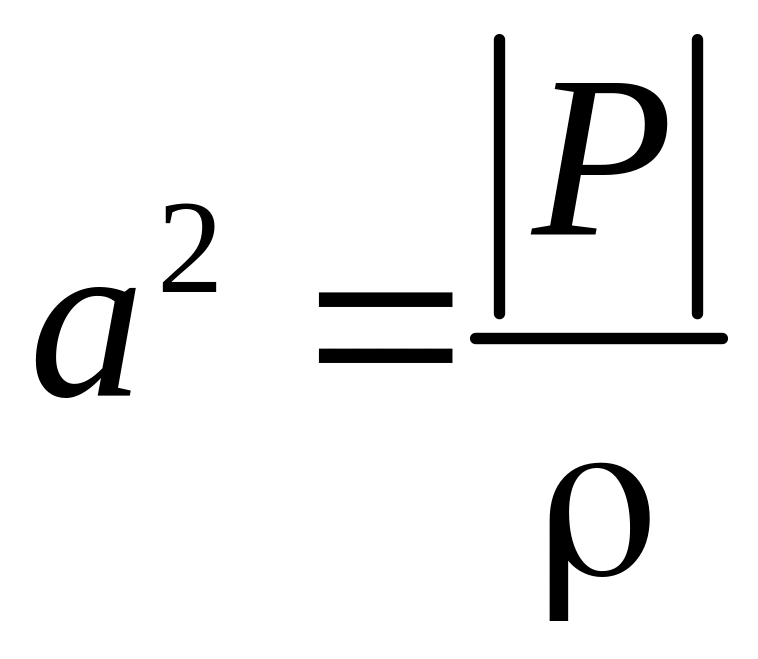Рівняння (4.4) є однорідним рівнянням - найпростішим рівнянням коливань струни або одномірним хвильовим рівнянням. Якщо збурення струни повторюються то у праву частину рівняння необхідно додати функцію , що визначає збурення струни. Тоді рівняння стає неоднорідним

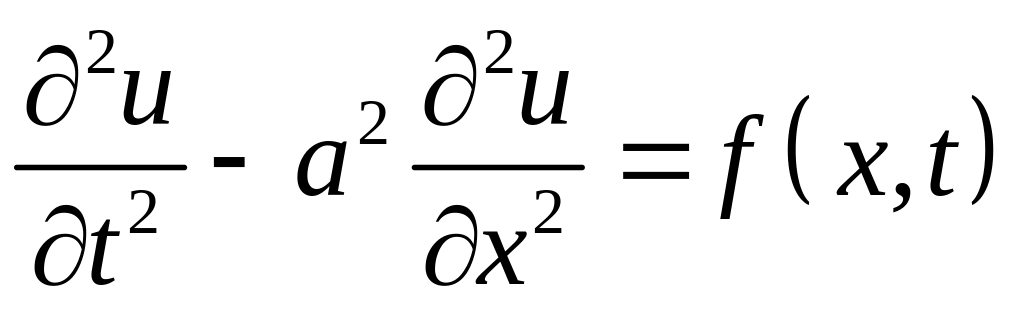
Для визначення форми струни у будь-який момент часу необхідно задати крайові умови, які включають у себе початкові та граничні умови. Початкові умови мають вигляд

; (4.5)

Граничні умови - це умови на кінцях струни. Якщо маємо жорстке закріплення, то граничні умови однорідні

. (4.6)

Якщо коливання виконує пружна плівка (мембрана), то рівняння буде двомірним.

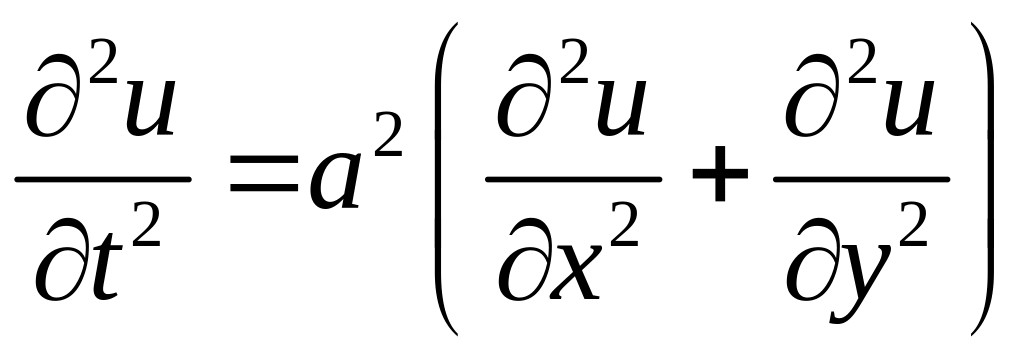. (4.7)

Тут початкові умови ставляться у вигляді

; . (4.8)

Так як мембрана закріплена уздовж лінії, що обмежує її границю , то гранична умова буде мати вигляд

Для поширення акустичних та електромагнітних хвиль за теорією Герца -Максвелла маємо тривимірне хвильове рівняння

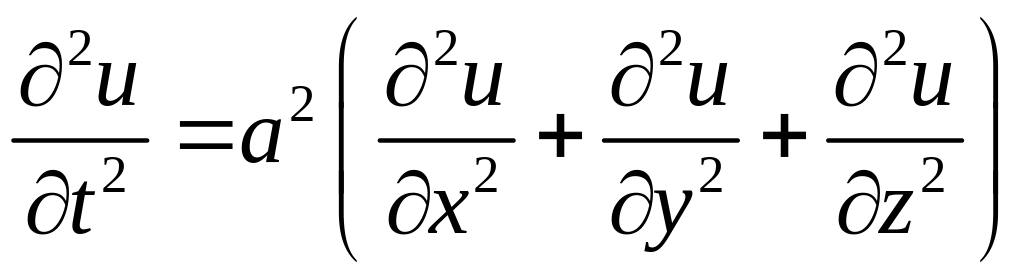, (4.9)

або у скороченому вигляді 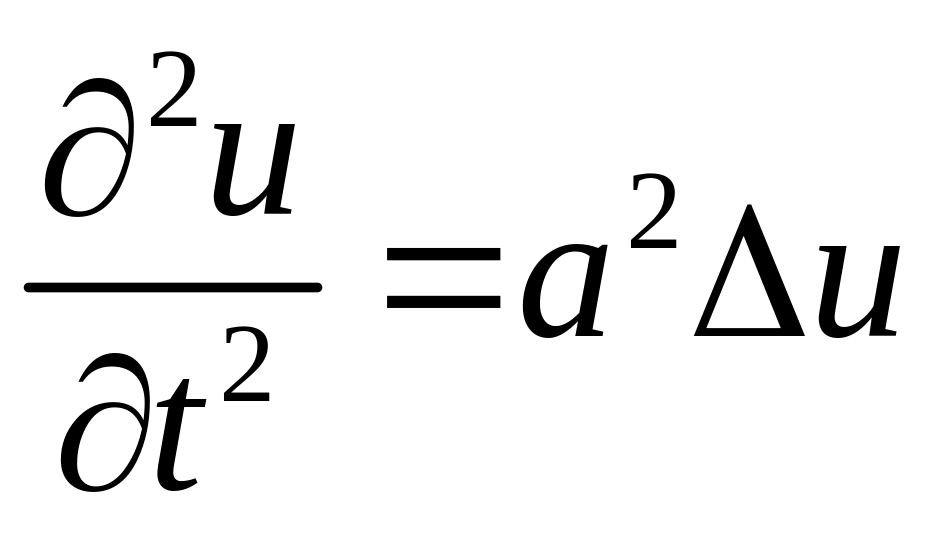, де 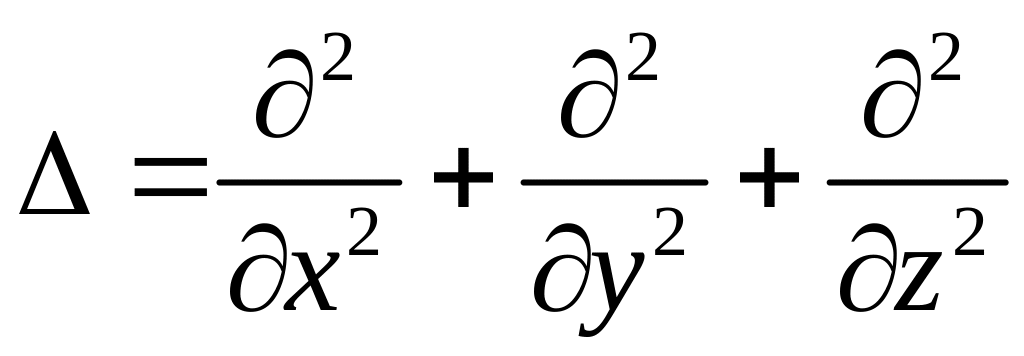– диференціальний оператор Лапласа. Таке ж рівняння описує рух рідини або газу у гідродинаміці. Тут – потенціал швидкостей руху точок, – швидкість поширення хвиль у середовищі. Початкові умови для задачі (4.9) мають вигляд

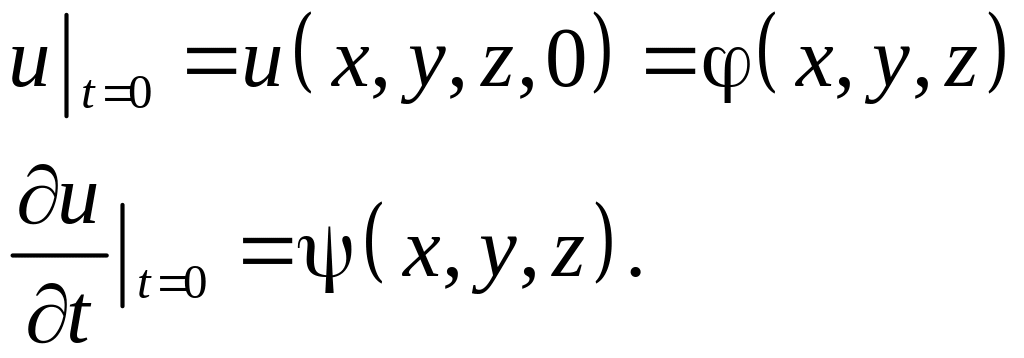(4.10)

Граничні умови визначають умови взаємодії на межі двох середовищ.

Для хвильового рівняння (4.4) мають місце три типи граничних умов. Найпростіші із них для лівого кінця струни мають вигляд.

Умова I роду – на границі задана функція.

Умова II роду – на границі задана похідна.

Умова III роду – на границі задана комбінація похідної та функції.

Аналогічно можуть бути сформульовані граничні умови на правому кінці . Більш складні граничні умови мають місце, наприклад, при пружному закріпленні, не підпорядкованому закону Гука, коли натяг на кінці є нелінійною функцією зміщення , наприклад, – нелінійна умова.

Можливі співвідношення між зміщенням і натягом на різних кінцях струни.

У задачах про коливання кільця, коли та представляють собою одну і ту ж саму фізичну точку, граничні умови набувають вигляду , , тобто зводяться до вимоги неперервності функцій та .

Відповідно граничним умовам формулюється перша друга та третя крайова задачі для рівняння гіперболічного типу.

Перша крайова задача для рівняння (4.4) формулюється так:

знайти функцію , визначену в області , , яка задовольняє рівнянню для , ,

початковим умовам ,

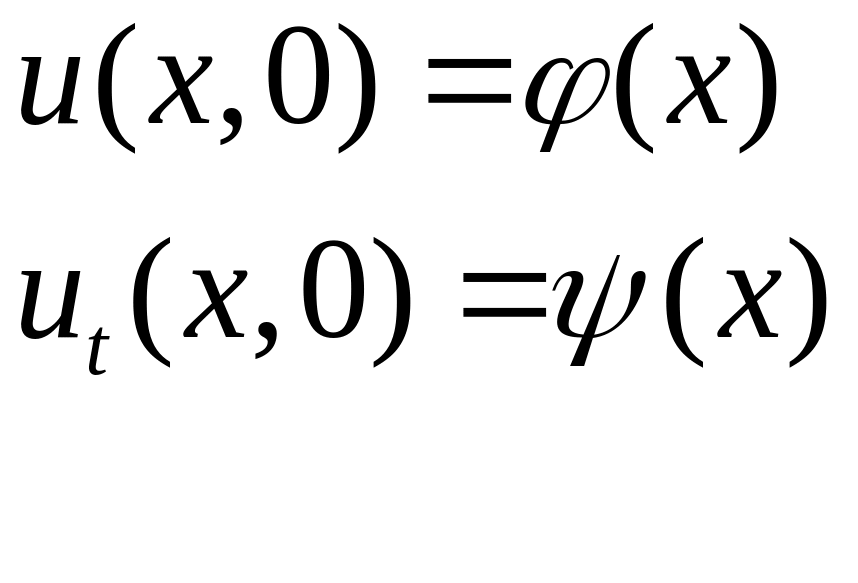та граничним умовам , .

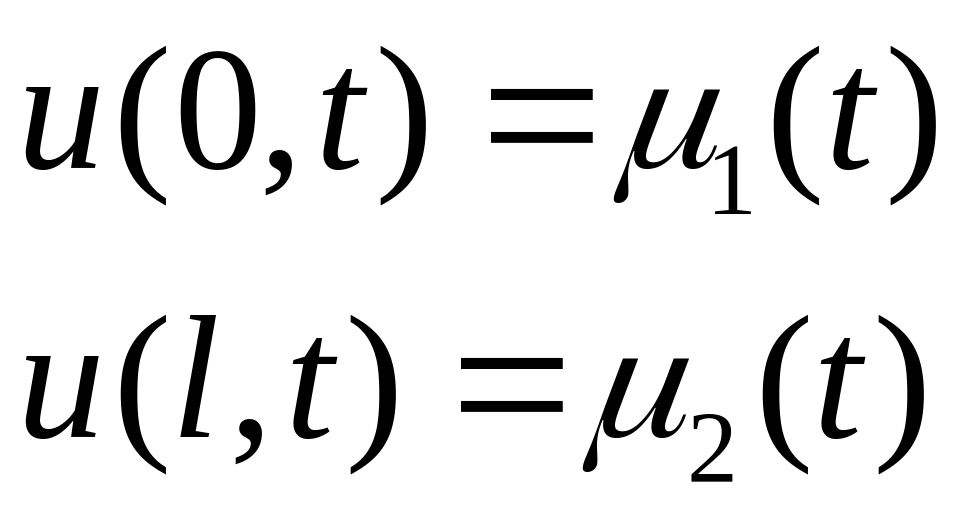Якщо в умові (4.1) доданко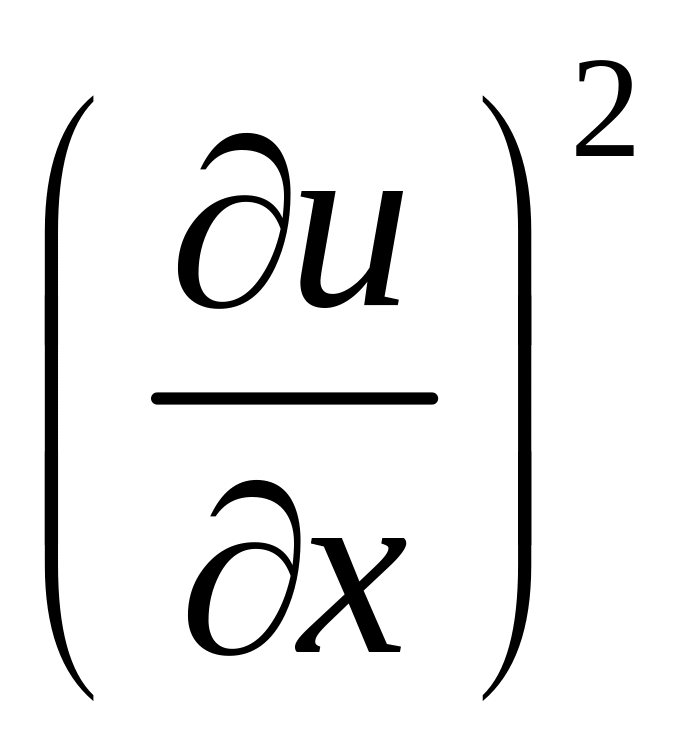м не нехтувати, то рівняння (4.4) буде нелінійним

.
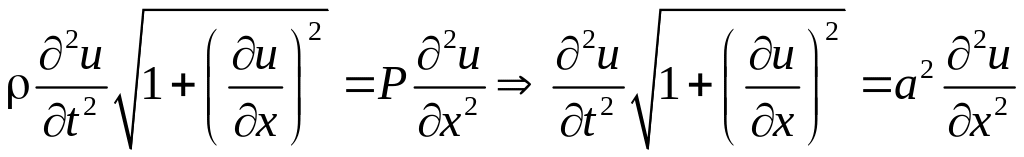