
- •Раздел 1. Электрические цепи с линейными элементами
- •Тема 1.1. Электрические цепи постоянного тока
- •Тема 1.2. Электрические цепи переменного тока
- •Вопросы для самоконтроля и задачи для самостоятельного решения
- •К вопросу «Измерение сопротивлений»
- •1. Делитель напряжения
- •2. Мост Уитстона
- •К вопросам «Измерение токов» и «Измерение напряжений»
- •Схемы с общим эмиттером и с общей базой
Тема 1.2. Электрические цепи переменного тока
Индуктивный и емкостной элементы. Методы расчета электрических цепей однофазного синусоидального тока. Методы расчета трехфазных цепей синусоидального тока. Переходные процессы в электрических цепях с линейными элементами.
Индуктивный элемент
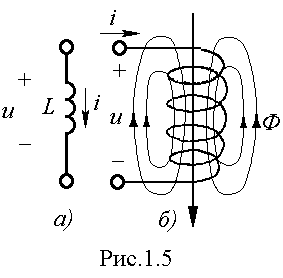
Индуктивным элементом электрической цепи называют такой идеализированный элемент, в котором происходит только запасание магнитной энергии, связанное с протеканием тока; потери и запасание электрической энергии отсутствуют. Условное графическое обозначение индуктивного элемента, основной количественной мерой которого является индуктивность, (или коэффициент самоиндукции) L, показано на рис. 1.5, а. Индуктивностью называют также сам элемент.
![]() , (1.9)
, (1.9)
где N – общее число витков катушки.
Так как согласно закону полного тока напряженность магнитного поля пропорциональна току, то потокосцепление при отсутствии ферромагнитных тел пропорционально величине тока:
![]() (1.10)
(1.10)
Индуктивность является коэффициентом пропорциональности между потокосцеплением и током и равна отношению L = /i. В системе СИ индуктивность измеряется в Генри (Гн). Будем принимать индуктивность постоянной величиной, не зависящей от тока и времени, что также является идеализацией и выполняется лишь приближенно.
Связь между током и напряжением в индуктивном элементе устанавливается на основе закона электромагнитной индукции: при изменении магнитного потока, сцепленного с контуром, в нем наводится электродвижущая сила, равная скорости изменения потокосцепления и направленная так, чтобы ток, вызванный ею, стремился воспрепятствовать изменению наводящего потока. Если ток, протекая в положительном направлении, нарастает так, что di/dt>0 и d/dt>0, то наведенная Э.Д.С. е должна иметь полярность (рис. 1.5, б), которая при отсутствии внешнего источника создавала бы ток, направленный навстречу току i.
Указанной полярности соответствует положительное напряжение пассивного элемента, которым представляется индуктивность. Поэтому интересующая нас связь между током и напряжением элемента согласно закону электромагнитной индукции имеет вид
![]() , (1.11)
, (1.11)
Напряжение на индуктивном элементе определяется скоростью изменения тока. При протекании через индуктивность постоянного тока поток не изменяется, напряжение равно нулю, что равносильно короткому замыканию вывода элемента.
Выражение (1.11) позволяет определить напряжение по заданному току. Если же задано напряжение, то, проинтегрировав обе части выражения (1.11) в пределах от - до t, получим, что ток в любой момент времени
![]() . (1.12)
. (1.12)
Выбор нижнего предела t = - при интегрировании вызван необходимостью суммирования всех изменений напряжения, имевших место до момента t, т. е. необходимостью учета всей предыстории элемента. Значение тока при t = - следует принимать равным нулю. Выражение(1.12) можно переписать в виде
![]() . (1.13)
. (1.13)
Здесь i(0) – начальный ток, т. е. значение тока в момент t = 0, которое учитывает все процессы в элементе до момента t = 0.
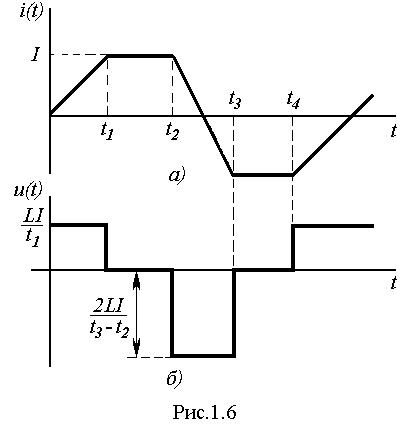
Можно рассматривать обратный случай, когда к индуктивности приложено напряжение в виде прямоугольных импульсов, показанных на рис. 1.6, б. В соответствии с законом электромагнитной индукции ток согласно (1.12) должен иметь трапецеидальную форму (рис. 1.6, а), которая при наличии начального тока будет смещена на величину этого тока.
Из соотношений (1.11) и (1.13) можно установить очень важное условие непрерывности потокосцепления и тока в момент приложения напряжения (t = 0) к индуктивному элементу: если амплитуда напряжения конечна, то потокосцепление должно быть непрерывным и не может меняться скачком: представив, согласно (1.13), потокосцепление в момент t = 0+ через начальное значение в момент t = 0-, имеем:
![]() . (1.14)
. (1.14)
Обозначив через L(+) и L(-) значения индуктивностей до и после переключений в цепи, это условие можно записать в виде
![]() . (1.15)
. (1.15)
Если в процессе коммутации индуктивность не изменяется (L(-) = L(+)), то ток является также непрерывной величиной и не может меняться скачком: I(0–) = I(0+). Если же при коммутации происходит изменение индуктивности, то, согласно (1.15), ток не является непрерывной величиной. Приведенные условия непрерывности потокосцепления и тока используются далее при определении произвольных постоянных интегрирования.
Если в момент коммутации выполняется условие непрерывности тока, то для этого момента (t = 0) индуктивность, очевидно, можно заменять источником тока с током i(0). В случае i(0) = 0 индуктивность для момента t = 0 должна представляться в виде разрыва.
Рассмотрим энергетические характеристики индуктивного элемента. С учетом соотношения (1.11) мощность
![]() . (1.16)
. (1.16)
При совпадении знаков тока и напряжения происходит запасание энергии и мощность положительна, при несовпадении знаков мощность отрицательна, что означает отдачу запасенной в элементе энергии.
Взяв интеграл от мощности в пределах от t = -, где ток следует полагать равным нулю, до t, где ток равен i, получаем энергию, запасенную в индуктивности:
![]() . (1.17)
. (1.17)
Энергия в индуктивности определяется величиной тока в данный момент: она пропорциональна квадрату тока и поэтому не может принимать отрицательных значений.
Емкостный элемент (конденсатор)
Под емкостным элементом электрической цепи понимают такой идеализированный элемент, в котором происходит только запасание электрической энергии, зависящей от напряжения, а потери и запасание магнитной энергии отсутствуют. Близким к этому идеальному устройству является электрический конденсатор с хорошим диэлектриком при относительно невысоких частотах.
В случае приложения к конденсатору напряжения на его обкладках появятся заряды, равные по величине и противоположные по знаку, и в диэлектрике между обкладками образуется связанное с этими зарядами электрическое поле. Так как напряженность электрического поля пропорциональна напряжению между обкладками, заряд на обкладках конденсатора будет пропорционален напряжению:
Для установления связи между током и напряжением в емкостном элементе достаточно продифференцировать выражение (1.18). В результате получим зависимость тока в емкости от напряжения на ней
![]() . (1.18)
. (1.18)
![]() . (1.19)
. (1.19)
Ток в емкостном, элементе определяется скоростью изменения напряжения. В случае приложения постоянного напряжения ток в емкости равен нулю и элемент должен представляться разрывом.
Если задан ток, то, проинтегрировав обе части выражения (1.19) в пределах от - до t, получим для напряжения на емкости
![]() , (1.20)
, (1.20)
где u(0) = q (0)/С – начальное напряжение на емкости (при t = 0), учитывающее все процессы до момент t = 0.
Напряжение емкостного элемента определяется значениями тока при t>0 и напряжения при t = 0; закон изменения тока до момента t = 0 не имеет значения.
Рассмотренный для индуктивного элемента пример можно применить и для емкостного элемента, если заменить на рис. 1.6, а, б ток напряжением, а напряжение током. В случае приложения напряжения трапецеидальной формы ток емкости (зарядный ток) будет иметь вид прямоугольных импульсов, положительных при нарастании напряжения (заряде емкости) и отрицательных при спадании напряжения (разряде емкости).
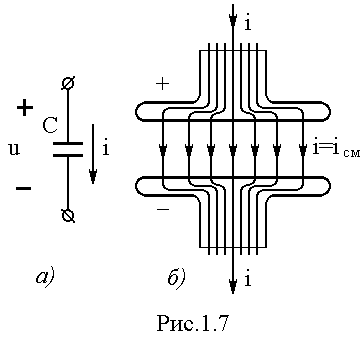
Необходимо отметить, что ток в емкости является током смещения, представляющим изменяющееся во времени электрическое поле; природа его иная, чем у тока проводимости, которого нет в диэлектрике. Лишь часть этого тока можно представлять в виде смещений связанных зарядов поляризованного диэлектрика. Как известно, ток смещения, так же как и ток проводимости, всегда связан с магнитным полем, и его следует рассматривать как выражение общего закона электромагнетизма, утверждающего, что изменяющееся во времени электрическое поле создает магнитное поле, т. е. эквивалентно току. Этот закон является двойственным закону электромагнитной индукции, утверждающему, что изменяющееся во времени магнитное поле создает электрическое поле. Только при введении токов смещения сохраняется замкнутость тока: линии тока смещения в диэлектрике являются .продолжением линий токов проводимости в обеих обкладках конденсатора (рис. 1.7, б).
Выражения (1.19) и (1.20) позволяют установить условие непрерывности заряда в емкостном элементе. При протекании в емкости тока конечной амплитуды заряд должен быть непрерывной функцией и не может меняться скачком: выразив, согласно(1.20), значение заряда в момент t = 0+ через значение в момент t= 0-, имеем
![]() . (1.21)
. (1.21)
Это условие можно записать через напряжение, если обозначить через С(-) и С(+) значения емкостей до и после коммутации:
![]() . (1.22)
. (1.22)
Если в процессе коммутации величина емкости не изменяется, (С(-) = С(+)), то напряжение на емкости также будет непрерывным-: u(0-) = u(0+). Приведенные условия непрерывности заряда и напряжения также используются далее при определении произвольных постоянных интегрирования.
Для момента t=0 емкостный элемент в силу непрерывности его напряжения можно заменять источником напряжения с напряжением u(0) или коротким замыканием, если u(0) = 0.
Мощность емкостного элемента
![]() . (1.23)
. (1.23)
Мощность положительна в интервалах нарастания энергии, когда энергия поступает от источника в элемент, отрицательна в интервалах убывания энергии, когда запасенная энергия отдается обратно источнику.
Интегрирование выражения (1.23) в пределах от - до t позволяет найти в предположении u(-) = 0 энергию, запасенную в емкости:
![]() . (1.24)
. (1.24)
Энергия в емкости определяется мгновенным значением напряжения: она пропорциональна квадрату напряжения и поэтому не может принимать отрицательных значений.
Дуальность элементов и их характеристик
В таблице даны соотношения между напряжениями и токами рассмотренных элементов, которые сокращенно называют вольтамперными характеристиками. Первый столбец дает напряжение элемента в зависимости от тока, второй – ток в зависимости от напряжения; в третьем приведены энергетические характеристики элементов.
Активное сопротивление |
uR=RiR |
iR=GuR |
PR=R(iR)2=G(uR)2 |
Индуктивность |
|
|
|
Емкость |
|
|
|
Соотношения, приведенные в этой таблице, позволяют установить определенную аналогию между ними. Сравнивая, например, выражения для напряжения на индуктивности и тока в емкости или выражения для энергии в этих же элементах, убеждаемся в их одинаковой структуре. Аналогия состоит в следующем. Если в первом выражении заменить напряжение током, ток напряжением и индуктивность емкостью, то оно переходит во второе. Если такую же замену произвести во втором выражении, то оно переходит в первое. Так же переходят друг в друга соотношения для активного сопротивления и активной проводимости при дополнительной взаимной замене R и G.
Два соотношения, обладающие указанным свойством взаимного перехода друг в друга, называются дуальными. При этом взаимно заменяемые величины являются дуальными величинами, а элементы, характеристики которых дуальны, – дуальными элементами. Следовательно, индуктивность и емкость, сопротивление и проводимость, а также источник напряжения и источник тока есть дуальные элементы. Понятие дуальности является взаимным: если элемент L дуален элементу С, то элемент С дуален L.
Взаимно дуальными являются следующие величины:
 . (1.25)
. (1.25)
Дуальность основных элементов приводит к тому, что дуальными могут быть цепи и их уравнения. В дальнейшем часто будет применяться это понятие. Приведем теперь кратко общие соображения о соотношении между реальными устройствами и их моделями в виде схем замещения, составленными из элементов R, L и С.
Введенные элементы пассивных цепей являются идеализированными элементами или математическими моделями. Их не следует смешивать с реальными прообразами – угольным сопротивлением, катушкой, конденсатором или батареей и генератором, которые наряду с главным, определяющим параметром, отображаемым одним из идеализированных элементов, обладают также другими, побочными или «паразитными» параметрами.
Индуктивный и емкостной элементы в цепях синусоидального тока
Тригонометрическая форма представления:
![]() ,
где Im
– амплитуда тока,
,
где Im
– амплитуда тока,
![]() – круговая частота,
– круговая частота,
![]() – фазовый сдвиг. Аналогично представляется
синусоидальное напряжение.
– фазовый сдвиг. Аналогично представляется
синусоидальное напряжение.
Согласно закону электромагнитной
индукции напряжение на индуктивном
элементе
![]() .
Подставляя выражение для тока и
напряжения, получим тригонометрическое
равенство
.
Подставляя выражение для тока и
напряжения, получим тригонометрическое
равенство
![]() . (1.26)
. (1.26)
Сопоставляя левую и правую части равенства (1.26), найдем следующие соотношения;
![]() ;
;
![]() . (1.27)
. (1.27)
Величина xL = L, имеющая размерность сопротивления, называется индуктивным сопротивлением. Из формулы, определяющей хL, следует, что индуктивное сопротивление прямо пропорционально частоте .
Мгновенная мощность р
цепи для случая
![]() ,
т.е.
,
т.е.
![]() имеет вид
имеет вид
![]() .
Активная мощность Р
= 0, реактивная мощность Q
= UI,
полная мощность S
= Q.
С учетом первого
соотношения (1.27) реактивную мощность
перепишем в виде
.
Активная мощность Р
= 0, реактивная мощность Q
= UI,
полная мощность S
= Q.
С учетом первого
соотношения (1.27) реактивную мощность
перепишем в виде
![]() .
.
В силу того что индуктивный элемент в цепи вызывает появление только реактивной мощности, индуктивное сопротивление является реактивным сопротивлением.
Емкостное сопротивление — сопротивление емкостного элемента переменному току. Оно так же, как и индуктивное сопротивление, является реактивным сопротивлением. Выполнив в общем виде расчет для индуктивного элемента, найдем следующие уравнения связи между параметрами напряжения и, приложенного к идеализированному конденсатору, и тока i, протекающего через него:
![]() ;
;
![]() . (1.28)
. (1.28)
Величина хC = 1/(С), имеющая размерность сопротивления, называется емкостным сопротивлением. Как видно из формулы, емкостное сопротивление обратно пропорционально частоте .
Мгновенную и другие мощности
запишем:
![]() ;
Р =
0; Q
= –UI;
S
= |Q|.
Формулу, определяющую
реактивную мощность, перепишем в виде
;
Р =
0; Q
= –UI;
S
= |Q|.
Формулу, определяющую
реактивную мощность, перепишем в виде
![]() .
.
Расчет цепей переменного тока
Комплексы электрических величин. Расчет цепей, состоящих из более чем одного элемента, выполняется, как правило, с использованием математического аппарата комплексных чисел.
Введем комплексные числа
![]() и
и
![]() ,
модули которых будут
равны амплитудам Um
и Im,
а аргументы – начальным фазам
,
модули которых будут
равны амплитудам Um
и Im,
а аргументы – начальным фазам
![]() и
и
![]() напряжения и тока соответственно:
напряжения и тока соответственно:
![]() ;
;
![]() , (1.29)
, (1.29)
где e — основание натурального логарифма.
Комплексные числа
![]() ,
,
![]() называются комплексной
амплитудой соответственно
напряжения и тока. В расчетах чаще всего
используются комплексные
действующие значения напряжения
называются комплексной
амплитудой соответственно
напряжения и тока. В расчетах чаще всего
используются комплексные
действующие значения напряжения
![]() и тока
и тока
![]() ,
которые определяются по формулам:
,
которые определяются по формулам:
![]() ;
;
![]() .
.
В дальнейшем комплексные величины , , , для краткости будем называть комплексами напряжения и тока.
Определим отношение комплекса
напряжения
![]() к комплексу
тока
,
которое обозначим
к комплексу
тока
,
которое обозначим
![]() :
:
![]() . (1.30)
. (1.30)
Здесь Z = U/I, = u – i – модуль и аргумент комплексного числа .
Таким образом, цепь переменного тока в самом общем случае характеризуется активным и реактивным сопротивлениями. Активное сопротивление является параметром резистивного элемента. Реактивным сопротивлением являются индуктивное и емкостное сопротивления – параметры L и С элементов, вызывающих появление в цепи реактивной мощности.
Уточним для случая, когда комплексы и относятся к одному и тому же участку цепи.
Комплексное сопротивление. Комплексное число , равное отношению комплекса напряжения к комплексу тока , принадлежащих одному и тому же участку цепи, называется комплексным сопротивлением этого участка.
На основании формулы (1.30), найдем комплексные сопротивления R, L и С элементов:
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, сопоставление параметров напряжения и тока, относящихся к R, L, С элементам, может быть определено с помощью комплексных чисел, которые мы назвали комплексными сопротивлениями элементов. Полученный результат (см. табл.) свидетельствует о целесообразности использования комплексных чисел при расчетах цепей переменного тока.
Элемент |
Z=U/I |
= u – i |
|
R |
R |
0° |
R |
L |
xL |
90° |
jxL |
С |
xC |
-90° |
-jxC |
Закон Ома в комплексной форме. Перепишем формулу (1.30) в виде
![]() . (1.31)
. (1.31)
Формула (1.31) определяет закон Ома в комплексной форме.
Описание электромагнитного состояния любого пассивного участка цепи, включая участки с L- и С-элементами, с помощью формулы (1.31) позволяет существенным образом упростить расчет цепей переменного тока.
Векторная диаграмма. При анализе установившегося электромагнитного состояния цепи переменного тока широко используется векторная диаграмма.
Векторной диаграммой называется совокупность векторов – комплексов , ( , ) напряжений и токов электрической цепи одной частоты, построенная на комплексной плоскости с учетом фазовых соотношений.
Векторная диаграмма цепи имеет большое практическое значение. Часто предварительное (качественное) построение векторной диаграммы помогает более грамотно подойти к расчету цепи.
Определение мгновенных
напряжений и токов по известным
комплексам. Из
векторной диаграммы следует, что проекции
векторов
![]() и
и
![]() на мнимую ось Оj
определяют мгновенные значения и
и i
для момента времени t
= 0. Пусть
теперь векторы
и
вращаются относительно
неподвижной системы координат 10j
с угловой
скоростью
против направления
движения часовой стрелки. Тогда проекции
вращающихся векторов
и
на ось 0j
в произвольный момент времени t1
определят мгновенные значения и
и i,
соответствующие моменту времени t
= t1.
на мнимую ось Оj
определяют мгновенные значения и
и i
для момента времени t
= 0. Пусть
теперь векторы
и
вращаются относительно
неподвижной системы координат 10j
с угловой
скоростью
против направления
движения часовой стрелки. Тогда проекции
вращающихся векторов
и
на ось 0j
в произвольный момент времени t1
определят мгновенные значения и
и i,
соответствующие моменту времени t
= t1.
Следовательно, между векторами и и функциями и и I существует взаимно однозначное соответствие, которое позволяет найти (определить при известной частоте ) и и i через известные и по формулам:
![]() ;
;
![]() , (1.32)
, (1.32)
где Im[…] – оператор выделения мнимой части комплексной функции, заключенной в квадратных скобках.
В выражениях (1.32) величины
![]() ,
,
![]() называются соответственно
комплексным мгновенным напряжением и
комплексным мгновенным током.
называются соответственно
комплексным мгновенным напряжением и
комплексным мгновенным током.
Законы Кирхгофа в комплексной форме. Запишем законы Кирхгофа в общем виде:
![]() ,
,
![]() . (1.33)
. (1.33)
(Во втором из равенств (1.33) в правую часть вынесены напряжения (ЭДС) источников питания, входящих в рассматриваемый контур)
С учетом формул (1.32) равенства (1.33) перепишем в следующем виде:
![]() ;
;
![]() . (1.34)
. (1.34)
Из векторного анализа известно, что сумма проекций векторов на какую-либо ось равна проекции вектора, равного сумме векторов. Следовательно,
![]() ;
;
![]() ;
;
![]() .
(1.35)
.
(1.35)
Таким образом, с учетом формул (1.35) равенства (1.34) возможны только в том случае, если
![]() ;
;
![]() . (1.36)
. (1.36)
Равенства (1.37) определяют законы Кирхгофа относительно комплексных мгновенных токов, напряжений и ЭДС.
Разделив левую и правую
части равенств (1.36) на
![]() ,
получим законы Кирхгофа относительно
комплексов
,
,
,
получим законы Кирхгофа относительно
комплексов
,
,
![]() :
:
![]() ;
;
![]() . (1.37)
. (1.37)
Если сравнить полученные законы Ома и Кирхгофа в комплексной форме с аналогичными законами для цепи постоянного тока, структурные отличия между ними не обнаружатся. Следовательно, расчет цепи переменного тока относительно комплексов сведется к решению системы алгебраических уравнений, составленных на основании законов Кирхгофа (1.37) и Ома (1.31).
Резонансный RLC-контур
Рис.1.8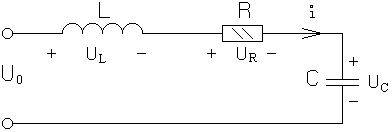
Применяя к последовательному контуру
(см. рис.1.8) закон токов Кирхгофа, приходим
к очевидному выводу о равенстве токов
во всех элементах:
![]() .
.
Применяя к единственному контуру закон
напряжений Кирхгофа, получим:
![]() .
.
Запишем уравнения напряжений для
элементов:
![]() .
.
Для получения уравнения цепи подставим в уравнение баланса напряжений уравнения элементов и заменим токи элементов общим контурным током. В результате получим общее интегро-дифференциальное уравнение с постоянными коэффициентами относительно контурного тока:
![]() .
.
Неизвестная переменная (ток в контуре) входит как под знаком производной, так и интеграла. Если продифференцировать полученное выражение, то получим эквивалентное линейное дифференциальное уравнение второго порядка:
![]() .
.
Рассуждая аналогичным образом для
параллельного контура (в котором будет
одинаковым напряжение на каждом элементе
и выполняется баланс токов), можно
получить уравнение относительно
напряжения
![]() ,
где i0 – ток,
отдаваемый в контур источником.
Продифференцировав данное выражение,
получим линейное дифференциальное
уравнение второго порядка для параллельного
контура (схему и уравнение следует
составить самостоятельно).
,
где i0 – ток,
отдаваемый в контур источником.
Продифференцировав данное выражение,
получим линейное дифференциальное
уравнение второго порядка для параллельного
контура (схему и уравнение следует
составить самостоятельно).
Полученные дифференциальные уравнения одинаковы по структуре, т.е. взаимно дуальны: переходят друг в друга при замене параметров и переменных на дуальные.
Вводя комплексные сопротивления
![]() ,
где j – мнимая единица,
– круговая частота,
равная 2f,
можно получить полное сопротивление
(комплексное!) Z,
например, параллельного контура:
,
где j – мнимая единица,
– круговая частота,
равная 2f,
можно получить полное сопротивление
(комплексное!) Z,
например, параллельного контура:
 (требуется получить самостоятельно).
Отсюда получим параметры резонансного
контура:
(требуется получить самостоятельно).
Отсюда получим параметры резонансного
контура:
– резонансная частота с затуханием:
![]() ;
;
– резонансная частота без затухания
(R=0):
![]() ;
;
– затухание контура:
![]() .
.
Для колебательного контура, в котором после начального возбуждения (сообщения контуру некоторой энергии) происходит обмен энергией между реактивными элементами (индуктивностью и емкостью), дифференциальные уравнения второго порядка аналогичны, но однородны, т.е. в правой части – нуль. Параметры колебательного контура получаются теми же самыми, что и для резонансного контура.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Общие сведения
Изменение схемы соединений
(например, включение и выключение
отдельных участков, подключение отдельных
элементов) называется коммутацией,
следствием которой может быть переход
от одного режима работы цепи к другому.
Практически переход or
одного режима работы к другому происходит
не мгновенно, а в течение некоторого
промежутка времени. Процессы, происходящие
в цепи в этот период времени, называются
переходными процессами.
Возникновение переходных
процессов объясняется тем, что каждому
состоянию электрической цепи соответствует
определенный запас энергии в электрическом
поле конденсатора (![]() )
немагнитном поле катушки индуктивности
(
)
немагнитном поле катушки индуктивности
(![]() ).
Переход к новому режиму
цепи связан с перераспределением этих
энергий между реактивными элементами
и с необратимыми
преобразованиями энергии в резистивных
элементах. Такие изменения энергий не
могут происходить мгновенно, т. е.
скачком, так как для изменения энергии
скачком необходима мощность p=dw/dt,
что лишено физического
смысла – цепей бесконечно большой
мощности не существует.
).
Переход к новому режиму
цепи связан с перераспределением этих
энергий между реактивными элементами
и с необратимыми
преобразованиями энергии в резистивных
элементах. Такие изменения энергий не
могут происходить мгновенно, т. е.
скачком, так как для изменения энергии
скачком необходима мощность p=dw/dt,
что лишено физического
смысла – цепей бесконечно большой
мощности не существует.
При наличии в цепи индуктивных и емкостных элементов переходный процесс длится теоретически бесконечно долго (пока полностью не закончится обмен энергиями между реактивными элементами), но практически продолжительность переходного процесса ограничена и часто исчисляется секундами или долями секунды.
Изучение переходных процессов имеет большое практическое значение, так как позволяет определять повышение токов и напряжений сверх номинальных значений из-за коммутаций в цепях с различными электротехническими устройствами (двигателями, трансформаторами, реле и т.п.). Во время переходного процесса токи и напряжения могут быть в несколько раз больше, чем в установившемся режиме, и привести к аварии. Подбирая значения параметров отдельных элементов и применяя специальные схемы их включения, можно ускорить или замедлить время переходного процесса, а также ограничить скачки тока и напряжения во время переходного процесса.
Законы коммутации. Начальные условия
Законы коммутации. Будем в дальнейшем считать, что коммутации (включения, отключения и т. д.) происходят мгновенно. Из закона сохранения энергии и требования конечного значения мгновенной мощности вытекает принцип непрерывности во времени потокосцепления и тока в индуктивном элементе, а также электрического заряда и напряжения на емкостном элементе. Это означает, что в первый момент после коммутации ток в индуктивном элементе (короче, индуктивности) равен току непосредственно перед коммутацией и напряжение на емкостном элементе (короче, емкости) в начальный момент времени после коммутации остается таким же, как непосредственно до коммутации, т.е. ток в индуктивном и напряжение на емкостном элементах не могут изменяться скачками. Эти положения и составляют два закона коммутации. В противном случае производная энергии соответственно магнитного и электрического полей, т.е. мгновенная мощность, получалась бы бесконечно большой, что не имеет физического смысла. Но, следует отметить, что токи и напряжения на резистивных элементах, ток в емкостном iC = CduC/dt и напряжение на индуктивном UL = Ldi/dt элементах могут изменяться скачком.
Начальные условия. Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями. Будем далее считать, что начало отсчета времени (t = 0) совпадает с моментом мгновенной коммутации. Значения потокосцепления и тока в индуктивности, заряда и напряжения на емкости непосредственно перед коммутацией (t = 0-) обозначим соответственно (0-) и iL(0-), q(0-) и uC(0-), а в начальный момент после коммутации (t = 0+) соответственно (0+) и iL(0+), q(0+) и uC(0+). При этом согласно законам коммутации (и в соответствии с (1.14) и (1.21)):
(0-) = (0+) или iL(0-) = iL(0+); (1.38)
q(0-) = q(0+) или uC(0-) = uC(0+). (1.39)
Из законов коммутации следует, что независимые начальные условия нужно определить из расчета электрической цепи до коммутации.
Если iL(0–) = 0 и UC(0–) = 0, то такие условия называются нулевыми независимыми начальными условиями.
Классический метод расчета переходных процессов
Общие положения. Переходные процессы в электрических цепях описываются системой дифференциальных уравнений, составленных по законам Кирхгофа для мгновенных значений напряжений и токов. Для несложных цепей эту систему уравнений можно исключением всех переменных, кроме одной, свести к одному дифференциальному уравнению для искомой величины, порядок которого не выше числа накопителей энергии (емкостных и индуктивных элементов). Для решения полученного таким преобразованием обыкновенного линейного неоднородного уравнения в математике разработаны различные методы, в частности классический, операторный, спектральный. В электротехнике для анализа переходных процессов в простых цепях широко применяется классический метод, который (по сравнению с другими) позволяет упростить рассмотрение физических процессов, происходящих в цепях.
Рис.1.9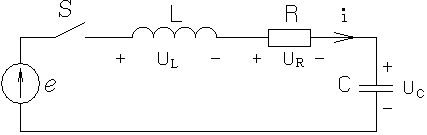
![]() (1.40,а)
(1.40,а)
или, так как
![]() ,
,
![]() , (1.40,б)
, (1.40,б)
т.е. получается линейное дифференциальное неоднородное уравнение второго порядка для напряжения на емкости uC.
Такого же вида уравнение
можно получить и для тока i,
если в (1.40,а) подставить
выражение
![]() ,
где А
– постоянная интегрирования.
После подстановки и дифференцирования
будем иметь:
,
где А
– постоянная интегрирования.
После подстановки и дифференцирования
будем иметь:
![]() . (1.41)
. (1.41)
Решение уравнений (1.40) и (1.41) представляется в виде суммы двух составляющих – установившейся и свободной:
![]() ; (1.42,а)
; (1.42,а)
![]() . (1.42,б)
. (1.42,б)
Установившиеся и свободные составляющие токов и напряжений. Частные решения uC уст, iуст неоднородных уравнений (1.40,б) и (1.41) определяются видом функции e(t) в правой части уравнения, т.е. для цепей с заданными периодическими или постоянными во времени ЭДС или токами источников определяются из расчета цепи, полученной после коммутации, методами расчета цепей переменного и постоянного тока.
Общие решения однородных уравнений – свободные составляющие (полученных из исходных уравнений (1.40,а) и (1.41) при равной нулю правой части) физически определяют процессы изменения энергии в реактивных элементах.
Общее решение каждого однородного дифференциального уравнения для последовательного контура (уравнения (1.40) и (1.41) при е=0) имеет два слагаемых
![]() ; (1.43,а)
; (1.43,а)
![]() , (1.43,б)
, (1.43,б)
здесь p1 и р2 – корни так называемого характеристического уравнения (предполагается, что они разные)
![]() (1.44)
(1.44)
для дифференциального уравнения (1.40,б) или
![]()
для дифференциального уравнения (1.41); А1 и А2 – постоянные интегрирования, определяемые из начальных условий.
Сумма установившейся и свободной составляющих является переходной величиной и для рассматриваемого контура определяется выражениями (1.42,а) и (1.42,б), которые справедливы и для момента времени t=0+:
![]() ,
,
![]() , (1.45)
, (1.45)
где
![]() и
и
![]() – независимые начальные условия.
– независимые начальные условия.
Из двух уравнений (1.45) можно
найти постоянные интегрирования, хотя
их четыре. Действительно, т.к.
![]() ,
то
,
то
![]() и
и
![]() .
.
Таким образом, классический метод расчета переходных процессов заключается в составлении дифференциальных уравнений для цепи, полученной после коммутации, в нахождении общего решения в виде суммы установившейся и свободной составляющих, определении корней характеристического уравнения и постоянных интегрирования из начальных условий.
По окончании переходного процесса (теоретически он длится бесконечно долго) токи и напряжения становятся равными установившимся, т. е. свободные составляющие постепенно затухают.
Переходные процессы в цепи с индуктивным и резистивным элементами
Рис.1.10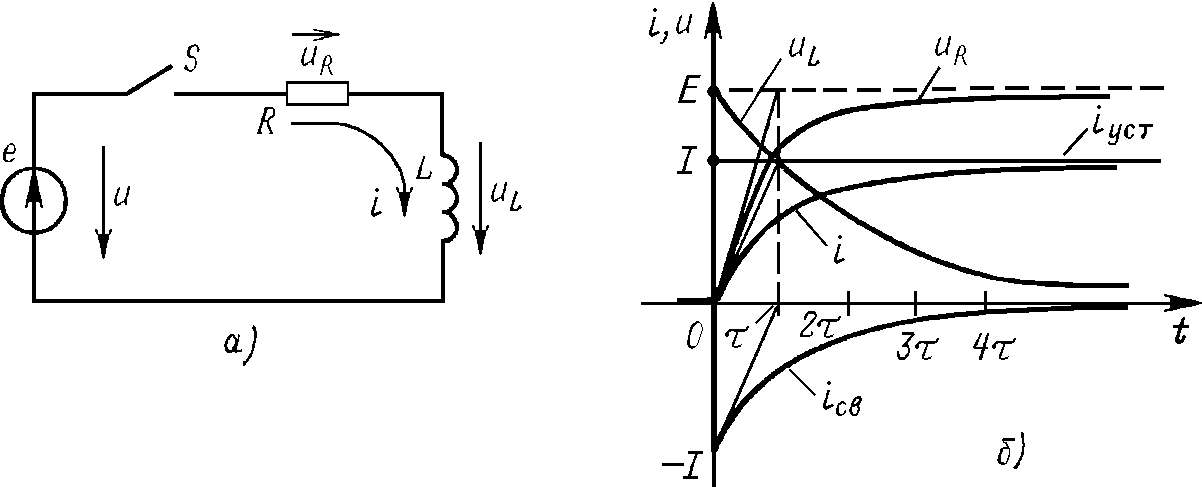
![]() . (1.46)
. (1.46)
В соответствии с (1.42) общее решение этого уравнения определяет ток в цепи:
![]() , (1.47)
, (1.47)
где р = –R/L – корень характеристического уравнения Lp+R=0.
Свободная составляющая
тока
![]() – это общее решение
однородного уравнения
– это общее решение
однородного уравнения
![]() .
.
Установившаяся составляющая
тока
![]() определяется из расчета цепи, полученной
после коммутации, при установившемся
режиме для заданной ЭДС e(t).
Таким образом, чтобы
получить выражение для расчета тока
переходного процесса, необходимо еще
определить ток установившегося режима
и постоянную интегрирования А.
Значение этих величин
определяется видом коммутации и законом
изменения ЭДС. Рассмотрим три случая:
1) включение цепи при постоянной ЭДС,
при е=Е
(рис.1.10,а), 2) отключение
цепи от источника постоянной ЭДС Е
с замыканием цепи через
резистор r
(рис.1.11,а), 3) включение цепи R,
L
(рис.1.10,a)
при источнике синусоидальной ЭДС
определяется из расчета цепи, полученной
после коммутации, при установившемся
режиме для заданной ЭДС e(t).
Таким образом, чтобы
получить выражение для расчета тока
переходного процесса, необходимо еще
определить ток установившегося режима
и постоянную интегрирования А.
Значение этих величин
определяется видом коммутации и законом
изменения ЭДС. Рассмотрим три случая:
1) включение цепи при постоянной ЭДС,
при е=Е
(рис.1.10,а), 2) отключение
цепи от источника постоянной ЭДС Е
с замыканием цепи через
резистор r
(рис.1.11,а), 3) включение цепи R,
L
(рис.1.10,a)
при источнике синусоидальной ЭДС
![]() .
.
Подключение цепи к источнику постоянной ЭДС. Установившийся ток =E/R, так как индуктивный элемент не имеет сопротивления при постоянном токе, и ток переходного процесса в соответствии с (1.47)
![]() . (1.48)
. (1.48)
При t=0+ (после коммутации) из (1.48) i(0+)=E/R+A. Следовательно, для определения постоянной интегрирования А нужно знать начальное значение тока i(0+). Так как в неразветвленной цепи ток во всех элементах один и тот же, то t(0+)=iL(0+). Но по первому закону коммутации ток в индуктивности не изменяется скачком, а до коммутации тока в цепи не было, т. е. iL(0+)= iL(0–)=0 и А=–E/R. Подставив найденное значение постоянной в (1.48), найдем ток переходного процесса:
![]() . (1.49)
. (1.49)
Здесь
![]() (имеет единицу времени
Гн/Ом = с) – постоянная
времени RL-цепи.
К моменту времени t=
свободная составляющая
тока
(имеет единицу времени
Гн/Ом = с) – постоянная
времени RL-цепи.
К моменту времени t=
свободная составляющая
тока
![]() уменьшится в e=2,718
раза.
уменьшится в e=2,718
раза.
Постоянная времени определяет
скорость изменения тока (или напряжения)
при переходном процессе. К моменту
времени (4…5)
переходный процесс практически
завершается, так как к этому моменту
времени
![]() .
.
В соответствии с (1.49) ток нарастает по экспоненциальному закону (стремится к установившемуся значению I) тем быстрее, чем меньше постоянная времени (рис. 1.10,б).
Получив зависимость (1.49), нетрудно определить напряжения на резисторе uR и индуктивном элементе uL во время переходного процесса
![]() ; (1.50)
; (1.50)
![]() . (1.51)
. (1.51)
Как следует из (1.50) и (1.51), в момент включения (t=0+) напряжение на индуктивном элементе равно ЭДС, а затем постепенно убывает и стремится к нулю. Это необходимо учитывать при анализе явлений в катушках индуктивности различных электротехнических устройств, например в системах зажигания двигателей внутреннего сгорания, или при регулировании времени срабатывания реле в цепи постоянного тока посредством включения последовательно с обмоткой резистора.
Пример 1. Неразветвленная RL-цепь (рис.1.10,а) включается на постоянное напряжение U=10 В. Определить постоянную времени цепи и длительность переходного процесса tп, если R=100 Ом, L=0,l Гн и допуск на отклонение от установившегося значения составляет 1%.
Решение
Постоянная времени
=L/R=0,1/100=10–3 с.
Переходный ток
![]() А.
А.
Переходный процесс можно
считать законченным, когда
![]() А, откуда
А, откуда
![]() ;
;
![]() и tп=4,610–3
с.
и tп=4,610–3
с.
Отключение RL-цепи от источника постоянной ЭДС и замыкание цепи резистором. Цепь RL отключается от источника постоянной ЭДС Е и при помощи переключателя S мгновенно замыкается резистором r (рис.1.11,а). По второму закону Кирхгофа для цепи после переключения
![]() . (1.52)
. (1.52)
Рис.1.11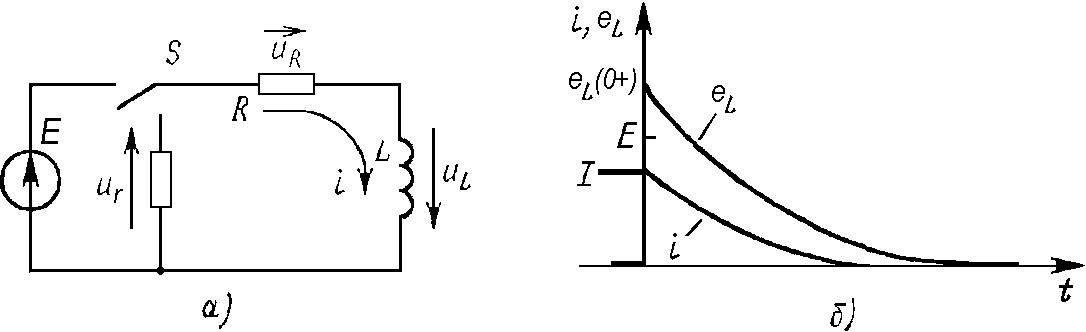
![]() ,
,
где р=–(R+r)/L – корень характеристического уравнения Lp+(R+r)=0; =L/(R+r) – постоянная времени цепи.
При t=0+ получается i(0+)=A, т.е. для определения постоянной интегрирования нужно найти начальное значение тока. До коммутации ток в цепи i=iL=E/R, т.е. iL(0–)=E/R=I, и по первому закону коммутации iL(0–)=iL(0+)=i(0+)=I, т.e. А=I. Итак,
![]() . (1.53)
. (1.53)
ЭДС самоидукции в катушке индуктивности
![]() . (1.54)
. (1.54)
ЭДС самоиндукции до коммутации не было, так как в цепи был постоянный ток I. В момент коммутации ЭДС возрастает скачком до значения E(R+r)/R, а затем убывает и стремится к нулю (рис.1.11,б), т. е. еL(0+) во столько раз больше ЭДС Е источника, во сколько раз увеличилось сопротивление цепи. В результате при переключении на индуктивном элементе может быть слишком большое напряжение (перенапряжение). Если размыкание RL-цепи рассматривать как ее замыкание через сопротивление r, то, казалось бы, по (1.54) напряжение UL(0+)= –eL(0+) должно в момент коммутации стремиться к бесконечности. В действительности под воздействием перенапряжения между контактами выключателя происходит пробой и образуется электрическая дуга, сопротивление которой окажется включенным в RL-цепь. Оно ограничит перенапряжение.
Рис.1.12
Подключение цепи к
источнику синусоидальной ЭДС.
Рассмотрим переходный процесс при
подключении RL-цепи
(рис.1.10,а) к
источнику синусоидальной ЭДС
![]() ,
где начальная фаза ЭДС
ip
показывает, при каком значении ЭДС
,
где начальная фаза ЭДС
ip
показывает, при каком значении ЭДС
![]() происходит включение. Установившаяся
составляющая тока также синусоидальная:
происходит включение. Установившаяся
составляющая тока также синусоидальная:
![]() , (1.55)
, (1.55)
где
![]() ;
;
![]() . (1.56)
. (1.56)
Соотношения (1.56) получены
на основании закона Ома в комплексной
форме
![]() ,
где Z
– полное комплексное сопротивление
рассматриваемой нами цепи, причем
,
где Z
– полное комплексное сопротивление
рассматриваемой нами цепи, причем
![]() .
.
Во время переходного процесса согласно (1.47) ток
![]() . (1.57)
. (1.57)
Начальные условия нулевые, так как iL(0–)= iL(0+)=0 (первый закон коммутации). При t=0+ согласно (1.57) i(0+)=iycт(0+)+icв(0+)=Im sin(t+–)+A=0, откуда A=–Im sin(–)
Подставив значение А в (1.57), окончательно получим:
![]() . (1.58)
. (1.58)
Рис.1.13
Переходные процессы в цепи с емкостным и резистивным элементами
Рис.1.14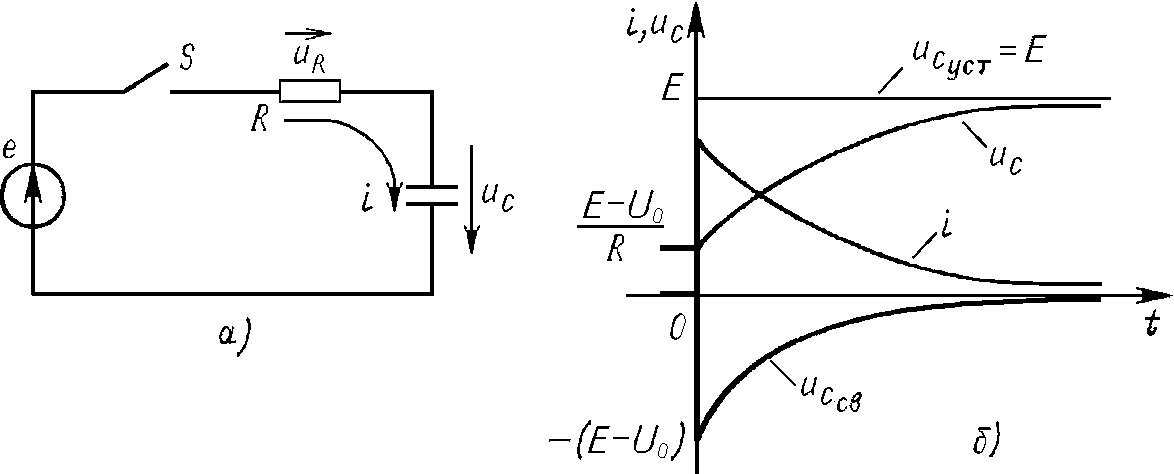
![]() :
:
![]() . (1.59)
. (1.59)
Общее решение этого уравнения имеет вид:
![]() , (1.60)
, (1.60)
здесь
![]() – свободная составляющая
напряжения на конденсаторе; p=–1/RC
– корень характеристического
уравнения RCp+1=0.
Установившаяся составляющая напряжения
на конденсаторе
– свободная составляющая
напряжения на конденсаторе; p=–1/RC
– корень характеристического
уравнения RCp+1=0.
Установившаяся составляющая напряжения
на конденсаторе
![]() зависит от вида ЭДС e
и схемы цепи после
коммутации.
зависит от вида ЭДС e
и схемы цепи после
коммутации.
Подключение RС-цепи
к источнику постоянной ЭДС
e=E=const.
По второму закону Кирхгофа для RС-цепи
(рис.1.14,a)
Ri+uC=E.
Постоянного тока не
может быть в RC-цепи
(конденсатор без потерь). Поэтому в
установившемся режиме
![]() и
и
![]() ,
т.е. согласно (1.60)
,
т.е. согласно (1.60)
![]() , (1.61)
, (1.61)
где =RC – постоянная времени RС-цепи.
Постоянная интегрирования А зависит от начальных условий. Если до коммутации конденсатор был заряжен до напряжения U0<E, т.е. uC(0–)=U0, то при t=0+ (непосредственно после коммутации) согласно второму закону коммутации uC(0–)= uC(0+)=U0 и по (1.61) uC(0+)=U0=E+A, откуда A=U0–Е. После подстановки постоянной в (1.61) получим:
![]() ; (1.62)
; (1.62)
ток
![]() . (1.63)
. (1.63)
Таким образом, напряжение на конденсаторе непрерывно нарастает от U0 до Е, а ток сначала увеличивается скачком от нулевого значения до i(0+)=(E–E0)/R, а затем уменьшается по экспоненциальному закону и стремится к нулю (рис.1.14,б).
Рис.1.15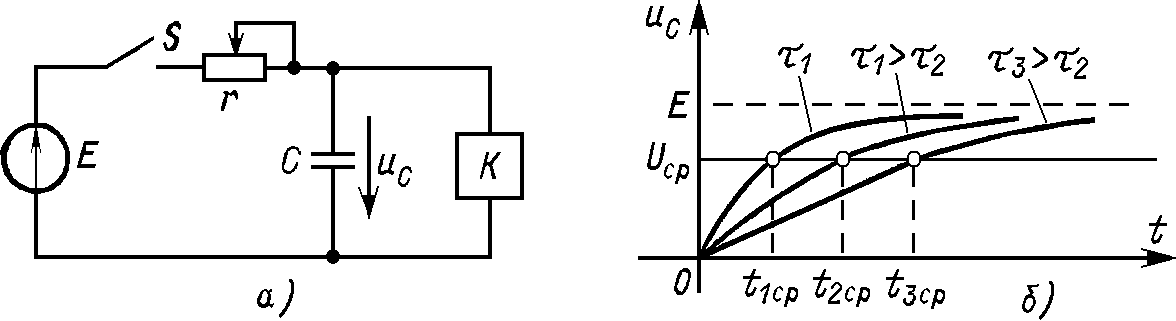
Рис.1.16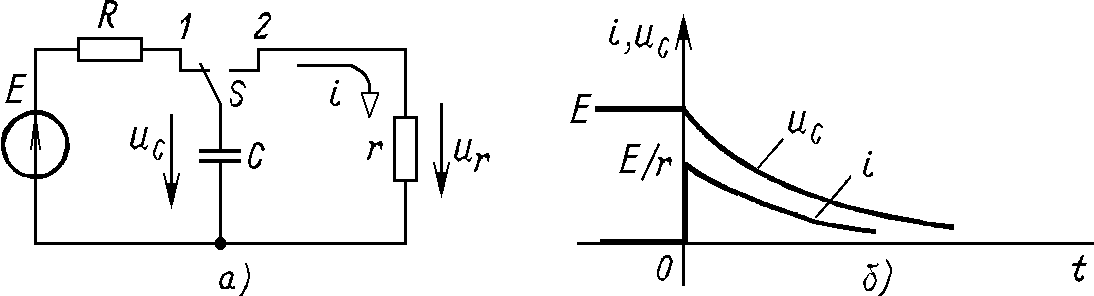
![]() ,
где принято во внимание, что ток разрядки
(рис.1.16,а) направлен противоположно току
зарядки (рис.1.14,а), т.е. напряжение и ток
конденсатора связаны не соотношением
,
где принято во внимание, что ток разрядки
(рис.1.16,а) направлен противоположно току
зарядки (рис.1.14,а), т.е. напряжение и ток
конденсатора связаны не соотношением
![]() ,
а
,
а
![]() .
Правая часть уравнения такая же, как у
(1.59), но уравнение однородное. Поэтому
uC
уст=0 и
.
Правая часть уравнения такая же, как у
(1.59), но уравнение однородное. Поэтому
uC
уст=0 и
![]() , (1.64)
, (1.64)
где корень характеристического уравнения р=–1/rС и постоянная времени = rС. Постоянную интегрирования А определим с учетом начальных условий: при t=0+ напряжение uC(0+)=uC(0–)=Е и по (1.64) uC(0+)=А, т.е. A=Е.
Подставив значение А в (1.64), получим:
![]() ; (1.65)
; (1.65)
![]() . (1.66)
. (1.66)
Напряжение на конденсаторе uC убывает от начального значения Е и стремится к нулю, а ток разрядки i скачком возрастает от 0 до значения i(0+)=E/r, а затем стремится к нулю по экспоненциальному закону.
Пример 2. Конденсатор емкостью С=15 мкФ заряжен до напряжения U=E=100 В (рис.1.16,а). После отключения конденсатора от источника он медленно разряжается через сопротивление собственной изоляции r. При этом через промежуток времени tр=42 с напряжение уменьшается в k=4 раза. Определить постоянную времени переходного процесса и сопротивление изоляции r.
Решение
Напряжение на конденсаторе
во время его разрядки в соответствии с
(1.65)
![]() .
Через время tр
напряжение станет равным
.
Через время tр
напряжение станет равным
![]() ,
откуда
,
откуда
![]() или
или
![]() .
Сопротивление изоляция r=/С=30/1510–6
Ом = 2 МОм.
.
Сопротивление изоляция r=/С=30/1510–6
Ом = 2 МОм.
Рис.1.17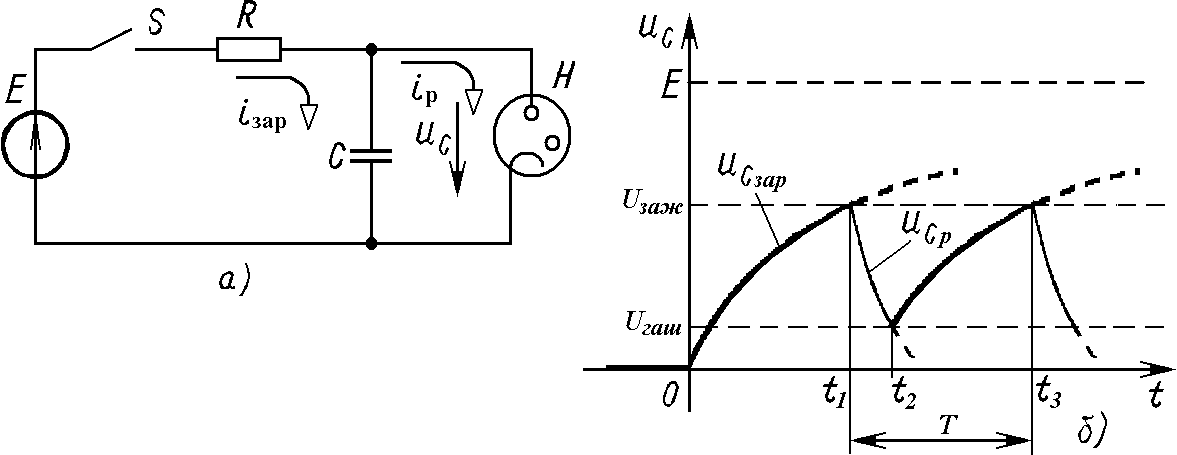
![]() ,
а во время дальнейшего периодического
процесса – по закону
,
а во время дальнейшего периодического
процесса – по закону
![]() ,
где время
,
где время
![]() отсчитывается от начала
очередной зарядки, a
Uгаш
– напряжение гашения
лампы. Постоянная времени цепи зарядки
зар=RC
подбором значения R
выбирается большой,
чтобы обеспечить почти линейное
нарастание напряжения (рис.1.17,б).
отсчитывается от начала
очередной зарядки, a
Uгаш
– напряжение гашения
лампы. Постоянная времени цепи зарядки
зар=RC
подбором значения R
выбирается большой,
чтобы обеспечить почти линейное
нарастание напряжения (рис.1.17,б).
При напряжении на конденсаторе
uСзар=Uзаж
происходит ионизация
газа в лампе и внутреннее сопротивление
ее резко уменьшается (Rл=r0),
и так как R>>r,
то происходит разрядка
конденсатора (рис.1.17,б) по закону (1.65)
![]() ,
где р=rС<<зар
и время t"
отсчитывается от начала
очередной разрядки. Напряжение на
конденсаторе, равное напряжению на
электродах лампы, быстро падает до
напряжения гашения Uгаш
и лампа гаснет. Начинается повторная
зарядка.
,
где р=rС<<зар
и время t"
отсчитывается от начала
очередной разрядки. Напряжение на
конденсаторе, равное напряжению на
электродах лампы, быстро падает до
напряжения гашения Uгаш
и лампа гаснет. Начинается повторная
зарядка.
Таким образом, напряжение на электродах лампы изменяется пилообразно и период колебаний Т определяется постоянными времени цепей зарядки и разрядки.
Переходные процессы в цепи с последовательным соединением резистора, конденсатора и катушки индуктивности
Дифференцирующие и интегрирующие цепи
Введение. В различных вычислительных и моделирующих устройствах, в схемах автоматики и электроники нередко необходимо интегрировать и дифференцировать изменяющиеся величины. Эти операции можно выполнить при помощи рассмотренных RL- и RС-цепей, однако чаще применяются RС-цепи, так как практически их проще реализовать.
Рис.1.18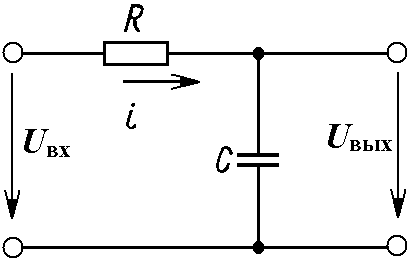
![]() , (1.67)
, (1.67)
то
![]() , (1.68)
, (1.68)
т.е. напряжение на выходе схемы пропорционально интегралу от напряжения на ее входе, если длительность интервала интегрирования много меньше . При синусоидальном входном напряжении необходимо выполнение условия UR>>UC или RI>>XCI, т. е. R>>ХC =1/С или RС>>1. Так как =2/Т, a RC=, то необходимо иметь 2>>Т, где Т – период синусоидального напряжения. Интегрирование будет тем точнее, чем больше постоянная времени цепи по сравнению с периодом входного напряжения Т. Однако из (1.68) следует, что при увеличении уменьшается значение выходного напряжения и для его увеличения приходится включать усилители. Если входное напряжение периодическое несинусоидальное, т. е. содержит высшие гармоники с частотой k1, то их интегрирование с ростом номера гармоники реализуется более точно, т.е. интегрирование периодических несинусоидальных сигналов возможно, если условие интегрирования удовлетворяется для основной гармоники.
Рис.1.19
![]() .
Так как uвых=Ri,
то
.
Так как uвых=Ri,
то
![]() , (1.69)
, (1.69)
т. е. uвых пропорционально производной напряжения на ее входе, если длительность сигнала много больше .
При синусоидальном входном напряжении необходимо выполнение условия UR<<UC или RI<<XCI, т.е. R<<ХC =1/С или RС<<1 и 2<<Т. Дифференцирование будет тем точнее, чем меньше постоянная времени цепи по сравнению с периодом входного напряжения Т. Однако из (1.69) следует, что при уменьшении уменьшается значение выходного напряжения и для его увеличения приходится включать усилители. Если входное напряжение периодическое несинусоидальное, т.е. имеет высшие гармоники, с частотой k1, то их дифференцирование с ростом номера гармоники k реализуется менее точно.
Моделирование
Общие сведения. Для исследования различных явлений и процессов, происходящих в сложных объектах, широко применяется моделирование, которое основано на аналогии математических моделей изучаемых объектов и соответствующих им электрических цепей и устройств. Процессы в механических, гидравлических и тепловых системах описываются дифференциальными уравнениями различного типа и порядка, многие из которых аналогичны уравнениям, составленным для мгновенных значений токов и напряжений в электрических цепях. Таким образом, применяя простые и точные методы анализа электрических цепей при различных режимах их работы, можно моделировать и изучать процессы, происходящие в сложных системах и объектах.
Принцип электрического моделирования. Принцип электрического моделирования заключается в следующем:
1) дается математическое описание изучаемого объекта или процесса с учетом всех его особенностей, т.е. составляется математическая модель объекта;
2) определяется электрическая цепь (или электромагнитная система), математическая модель которой аналогична математической модели изучаемого объекта, т. е. составляется электрическая модель изучаемого объекта;
3) на электрической модели аналитически или экспериментально выполняются исследования, по результатам которых методом аналогий определяются величины и процессы, происходящие в изучаемой системе или объекте.
Например, сила инерции J тела массой m при прямолинейном движении со скоростью v определяется выражением
![]() . (1.70)
. (1.70)
Электрической моделью этого процесса может быть закон электромагнитной индукции
![]() . (1.71)
. (1.71)
Рис.1.20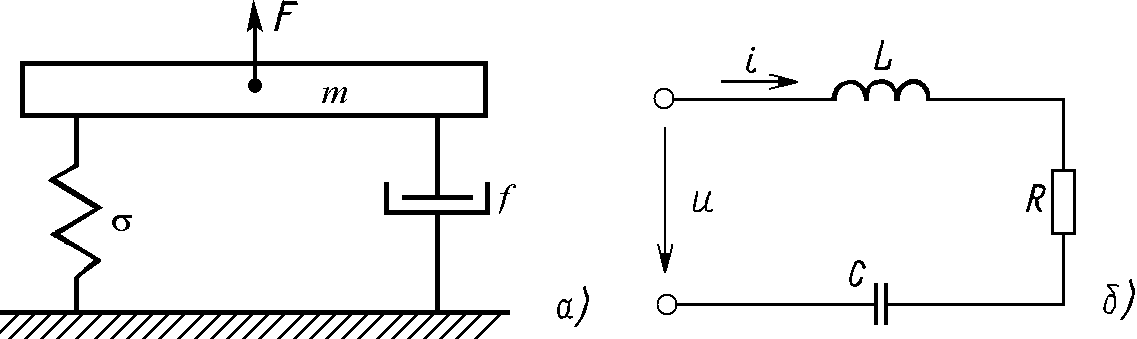
![]() ,
демпфирующей силой или силой трения fv
и силой упругости пружины
,
демпфирующей силой или силой трения fv
и силой упругости пружины
![]() .
.
Процесс в этой системе описывается уравнением
![]() (1.72)
(1.72)
или, если в это уравнение вместо скорости ввести перемещение v=dx/dt,
![]() . (1.73)
. (1.73)
Электрической моделью этой механической системы, движение в которой описывается обыкновенным дифференциальным уравнением второго порядка, является RLС-контур (рис.1.20,б). Согласно второму закону Кирхгофа для мгновенных значений тока и напряжений дифференциальное уравнение контура:
![]() .
.
Если в него вместо тока i=dq/dt ввести заряд, то получим:
![]() . (1.74)
. (1.74)
Из сравнения уравнений (1.73) и (1.74) видно, что представленная на рис.1.20,б электрическая цепь является аналогом механической системы по рис.1.20,а.
Переходные процессы в цепи с последовательным соединением резистора, конденсатора и катушки индуктивности
Переходный процесс в последовательной цепи RLС. Переходный процесс (рис.1.9) описывается дифференциальным уравнением (1.40,б) или (1.41), решение которого может быть представлено суммой установившейся и свободной составляющих. Так, для напряжения на емкости в соответствии с (1.42,а)
![]() , (1.75)
, (1.75)
здесь р1 и р2 – корни характеристического уравнения (1.44):
![]() . (1.76,а)
. (1.76,а)
В зависимости от соотношения
параметров корни могут быть действительными
различными (при R2/4L2>1/LC
или R>2![]() ),
действительными равными (р1=р2
при R=2)
и комплексными сопряженными
(при R<2):
),
действительными равными (р1=р2
при R=2)
и комплексными сопряженными
(при R<2):
![]() . (1.76,б)
. (1.76,б)
В первом и втором случаях процесс в цепи апериодический (экспоненциальные функции), в последнем – колебательный, причем
![]() и
и
![]() (1.77)
(1.77)
– коэффициент затухания и
угловая частота собственных затухающих
колебаний периодического переходного
процесса; 0=![]() – резонансная частота последовательного
RLС-контура.
– резонансная частота последовательного
RLС-контура.
Значение uCуст
определяется из расчета цепи (см. рис.1.9)
после коммутации в установившемся
режиме и зависит от вида ЭДС е,
постоянные интегрирования
![]() и
и
![]() определяются начальными условиями с
применением законов коммутации.
определяются начальными условиями с
применением законов коммутации.
Подключение RLС-цепи к источнику постоянной ЭДС е=Е. В установившемся режиме uCуст=E, iуст=0 и согласно (1.75) при различных корнях (p1p2)
![]() . (1.78)
. (1.78)
Ток в цепи
![]() . (1.79)
. (1.79)
Определим постоянные интегрирования и при нулевых начальных условиях: uC(0+)=0 (конденсатор не был заряжен). Из законов коммутации следует, что uC(0+)=иC(0–)=0 и i(0+) = =iL(0+)=iL(0–)=0 (напряжение на емкости и ток в индуктивности не изменяются скачком, а до коммутации они были равны нулю). Следовательно, согласно (1.78) и (1.79) при t=0+,
![]() ;
;
![]() .
.
Из решения этой системы определяются постоянные интегрирования:
![]() ;
;
![]() . (1.80)
. (1.80)
Подставив значение и в (1.78) и (1.79), получим выражение для напряжения на емкости и тока в цепи
![]() ; (1.81)
; (1.81)
![]() . (1.82)
. (1.82)
Из (1.81) и (1.82) следует, что характер переходного процесса определяется корнями характеристического уравнения р1 и р2, т.е. соотношением параметров R и .
Апериодический процесс.
Как указывалось (1.77), при R>2![]() корни р1
и р2
– действительные
отрицательные числа и решения (1.81) и
(1.82) содержат разности двух убывающих
экспоненциальных функций – апериодический
переходный процесс (рис.1.21,а).
корни р1
и р2
– действительные
отрицательные числа и решения (1.81) и
(1.82) содержат разности двух убывающих
экспоненциальных функций – апериодический
переходный процесс (рис.1.21,а).
Колебательный процесс. При R<2 корни р1 и р2 – комплексные сопряженные. При этом после подстановки в (1.81), (1.82) комплексных корней р1=–+jc и р2=––jc и применения формулы Эйлера эти выражения преобразуются к виду:
![]() ; (1.83)
; (1.83)
![]() , (1.84)
, (1.84)
где =arctgc/.
Рис.1.21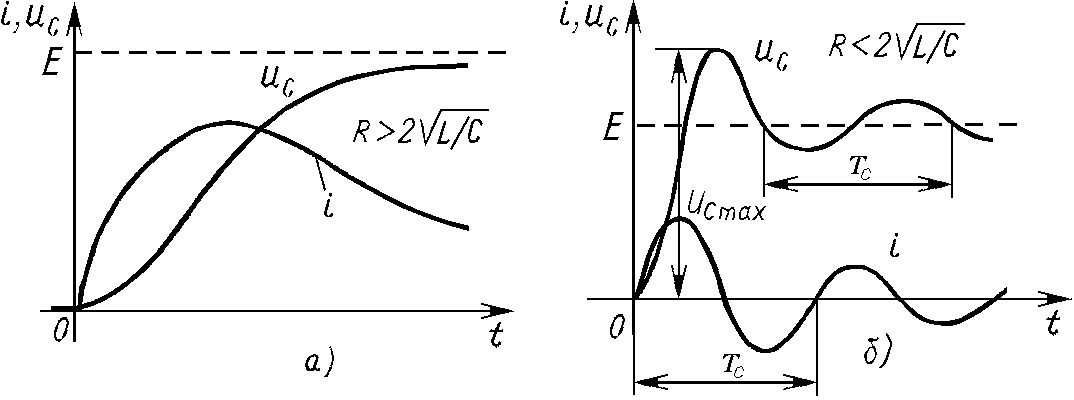
Скорость убывания амплитуд характеризуется декрементом колебаний =еТс, который равен отношению максимальных значений тока в моменты t и t+Тс, где Тс = 2/c – период колебаний. Величина ln=ln еТс=Тс называется логарифмическим декрементом колебаний.
Чем меньше коэффициент затухания по сравнению с c, тем медленнее затухает переходный процесс. После завершения переходного процесса (теоретически он длится бесконечно долго) независимо от его характера ток в цепи будет равен нулю, а напряжение на конденсаторе равно ЭДС (uCуст=E).
