Линейные операторы

Пусть X,Y – линейные нормированные пространства. Понятие линейного оператора А: XY означает справедливость тождеств А(x₁+x₂) = А(x₁) + А(x₂), А(x) = А(x). Нас будут интересовать непрерывные линейные операторы. Их множество будем обозначать символом L(X,Y). В этом пункте в частности будет установлено, что L(X,Y) можно наделить структурой линейного нормированного пространства. Приведем несколько примеров.

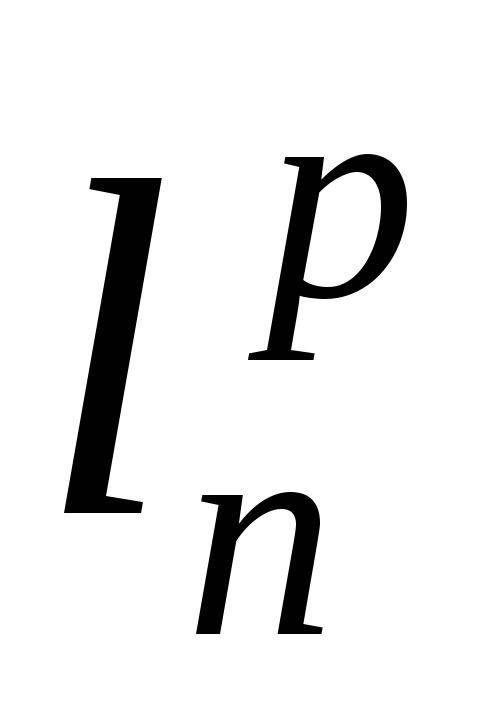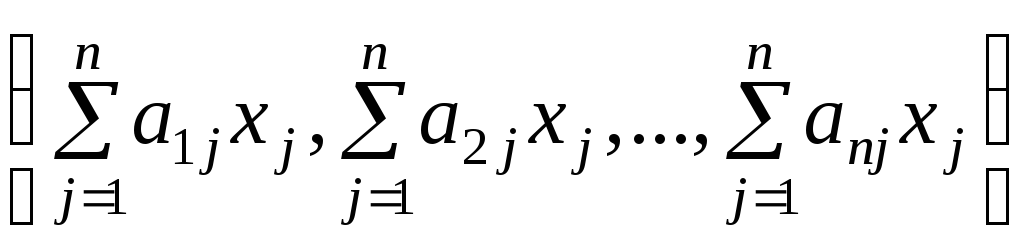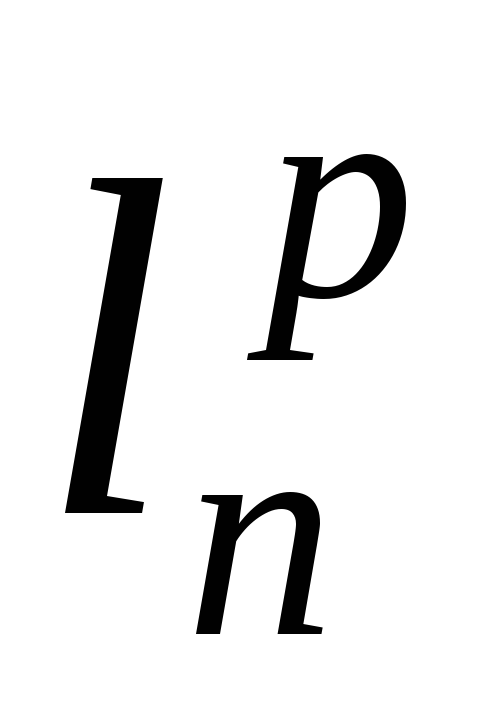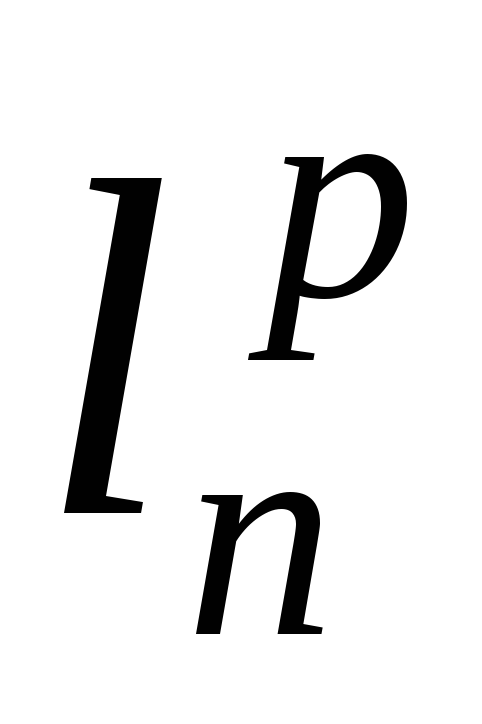
1. Рассмотрим квадратную матрицу А = (а_ij) (i=1,2,…,n; j=1,2,…,n). Рассмотрим отображение А: , действующее по правилуА(х₁,…,х_n) = . Из свойств матриц и векторов следует линейность оператора А. Напомним что сходимость в пространстве покоординатная, т.е.х⁽ⁿ⁾х⁽⁰⁾, если приi=1,…,n. Отсюда следует, что А(х⁽ⁿ⁾)  А(х⁽⁰⁾), т.е. оператор А непрерывный. Обратно, любое линейное отображение А: 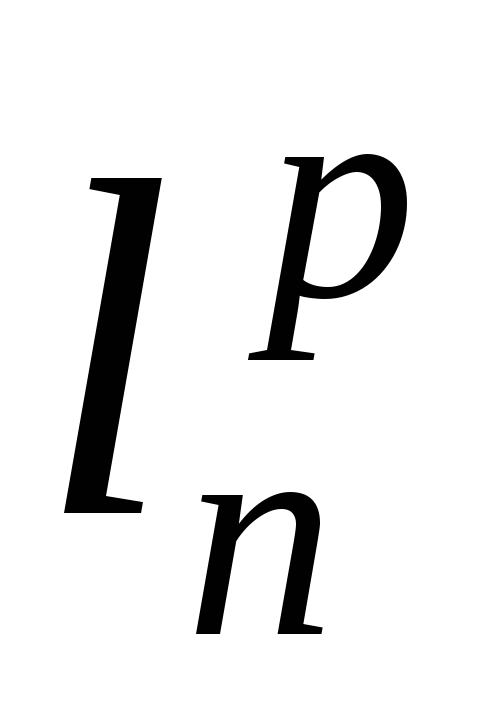 порождается некоторой матрицейА и автоматически является непрерывным.

2. Пусть K(t,s) функция, непрерывная на квадрате 0  t  1, 0  s  1. Сопоставим функции х(t) C функцию y(s) =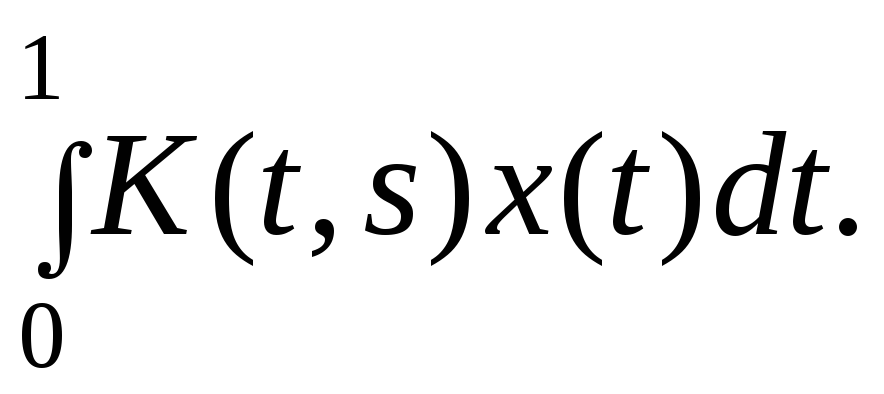Функцияy(s) непрерывная, т.е. y(s) C. Тем самым определен оператор A: CC. Его линейность следует из свойств интеграла. Далее, если (х₁,х₂) = maxх₁(t) х₂(t)<, то y₁(t)y₂(t)

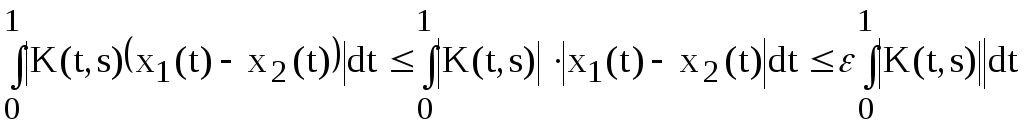
Это неравенство означает, что рассматриваемый оператор непрерывный. Такой оператор называется интегральным с ядром K(t,s).

ОПРЕДЕЛЕНИЕ 20. Линейный оператор А: X  Y называется ограниченным, если существует такое положительное число Р, что ||Аx||  Р||x||. Здесь ||Аx||  норма элемента в пространстве Y, ||x||  норма элемента в пространстве X.

ТЕОРЕМА 13. Ограниченность линейного оператора равносильна его непрерывности.

Удивительно, что множество линейных непрерывных операторов L(X,Y) можно наделить структурой линейного нормированного пространства.

Если А,B  L(X,Y), то суммой А+B линейных операторов называется оператор, действующий по правилу (А+B)(х) = Ах +Bх.

Если АL(X,Y), R, то произведением оператора на число называется оператор (А)(х) = (Ах). Поскольку в пространстве Y выполняются аксиомы линейного пространства, то множество L(X,Y) с введенными операциями является линейным пространством. Нулевым является оператор 0(х) = 0 для всех х.

Определим норму оператора как . Поскольку оператор ограниченный, то ||Аx||  Р||x|| при некотором Р, откуда число Р является верхней гранью множества {||Аx||: ||x||  1}, т.е. по теореме о точной верхней грани норма определена.

ПРЕДЛОЖЕНИЕ 19. Определенная функция действительно является нормой.

Поскольку множество линейных непрерывных отображений имеет структуру линейного нормированного пространства, к нему применимы все результаты предыдущего раздела. Пример:

ТЕОРЕМА 14. Если Y – банахово пространства, то и пространство L(X,Y) банахово.

Сопряженные пространства и слабая сходимость

Линейный оператор А: XR называется линейным функционалом. Пространство L(X, R) банахово (п. Error: Reference source not found), поскольку пространство вещественных чисел полное. Линейные ограниченные функционалы будем обозначать f(x). Как и раньше, норма линейного функционала определяется формулой .

ОПРЕДЕЛЕНИЕ 21. Пространство L(X, R) называется пространством, сопряженным к X и обозначается X*.

Конечномерные пространства.

Если (a₁,…,a_n) базис в п-мерном пространстве L, то линейный функционал f однозначно задается значениями (f(a₁),…, f(a_n)), поскольку для любого вектора значение функционала задается формулой. Мы будем использовать обозначениеf_i = f(a_i). Обратно, любой набор п чисел (f₁,…, f_n) задает линейный оператор в п-мерном пространстве описанным образом. Таким образом, пространством, сопряженным с п-мерным, является также п-мерное пространство. По сути, это описание на новом языке факта, который излагался в курсе линейной алгебры. Но теперь этого мало: мы рассматриваем пространства, наделенные нормой.

При p > 1 пространством, сопряженным к , является пространство, гдеЕслиp=2, то и q=2, т.е. пространство является сопряженным к самому себе. Этот факт будет далее обобщен.

Сопряженным к пространству является пространство. Действительно,

Пространства последовательностей.

Ограничимся формулировками некоторых результатов. При p>1 (l^p)*= l^q, где

(l¹)*=m. При этом, m*l¹.

Функциональные пространства.

Сопряженным к пространству С является пространство функций с ограниченной вариацией (подробности опускаем). К пополненному пространству L^p сопряженным является пространство L^q (p и q связаны обычным соотношением примера 1).

Гильбертовы пространства.

ТЕОРЕМА 15. Пространство, сопряженное к гильбертову пространству Н, изометрично Н.

ОПРЕДЕЛЕНИЕ 22. Последовательность {x_n} в линейном нормированном пространстве слабо сходится к вектору x₀, если для любого непрерывного функционала f справедливо утверждение f (x_n)  f (x₀).

Из непрерывности функционала следует, что из условия x_nx₀ по норме (в старом смысле) следует слабая сходимость. Приведем пример, который показывает, что обратное неверно.

Рассмотрим в гильбертовом пространстве l² последовательность векторов х₁=(1,0,…,0,…), х₂=(0,1,0,…,0,…),… (у вектора х_n п-я координата равна единице, остальные нулевые). Отмечалось (п. Error: Reference source not found), что эта последовательность не сходится в метрике пространства l². Пусть fl². Тогда (f,х_n)= f_n0, поскольку ряд сходится. Тем самымх_n слабо сходится к 0.