4. Компактные метрические пространства

ОПРЕДЕЛЕНИЕ 12. Метрическое пространство Х называется компактным, если из всякой последовательности в Х можно извлечь сходящуюся подпоследовательность. Компактное подпространство метрического пространства будем называть также компактным множеством.

ПРЕДЛОЖЕНИЕ 8. Компактное пространство является ограниченным.

ПРЕДЛОЖЕНИЕ 9. Компактное подпространство Y метрического пространства Х является замкнутым.

ТЕОРЕМА 3. Для того чтобы подпространство Y пространства было компактным, необходимо и достаточно, чтобы оно было замкнутым и ограниченным.

В других пространствах это утверждение неверно. Так, в дискретном пространстве компактные множества только одноточечные, хотя все подпространства замкнутые и ограниченные. В пространстве т множество векторов, описанное в примере п. Error: Reference source not found, также замкнутое и ограниченное, но не компактное.

ТЕОРЕМА 4 (Кантор). Любая вложенная последовательность компактных подмножеств в метрическом пространстве имеет непустое пересечение.

ТЕОРЕМА 5. Образ компактного метрического пространства X при непрерывном отображении является компактным.

Важный частный случай. Если f:XR – непрерывное отображение компактного пространства в множество вещественных чисел, то образ f(X) компактен. Но любое компактное подмножество прямой является замкнутым и ограниченным (теорема Больцано-Вейерштрасса). Следовательно, вещественная непрерывная функция, определенная на компактном метрическом пространстве, имеет наибольшее и наименьшее значения – обобщение теоремы Вейерштрасса из математического анализа.

ЗАМЕЧАНИЯ. 1. Прообраз компактного множества при непрерывном отображении может не быть компактным. Например, функция sin(x) отображает некомпактное пространство () на компактное [1,1].

2. В теореме компактность нельзя заменить полнотой. Например, функция отображает полное пространство [1,) на неполное (0, 1].

Поясним связь между понятиями замкнутости, полноты и компактности.

1. Замкнутость является свойством внешним, т.е. предполагается наличие объемлющего метрического пространства. Любое метрическое пространство является собственным замкнутым подмножеством. Компактность и полнота являются внутренними свойствами метрических пространств.

2. Из компактности следует полнота, обратное неверно. Пример  пространство R.

3. В то же время, полное подпространство является замкнутым.

Линейные нормированные пространства

ОПРЕДЕЛЕНИЕ 13. Множество Х называется линейным нормированным пространством, если

1. X является линейным пространством, т.е. для него определены операции сложения x+y и умножения векторов на числа x, обладающие следующими свойствами:

x+y = y+x;

(x+y)+z = y+(x+z);

Существует такой элемент (нулевой) 0  X, что x+0 = x для любого x;

Для всякого xX существует обратный (x), т.е. такой, что x+(x) = 0;

()x = (x);

(+)x = x+x;

(x+y) = x+y

1x = x.

2. На Х определена вещественнозначная функция ||х|| (норма), которая обладает следующими свойствами:

- ||х||  0, причем ||х|| = 0 только при х = 0,

- ||х|| = ||х||,

- ||х+y||  ||х||+||y||.

Наличие нормы позволяет ввести метрику на Х: (x,y) = ||хy||.

ПРЕДЛОЖЕНИЕ 10. Величина (x,y) обладает свойствами метрики.

Очевидно, что так определенная метрика сохраняется при сдвигах, т.е. выполняется свойство (x,y) = (x+z,y+z). Следует иметь в виду, что не всякая метрика в линейном пространстве, обладающая этим свойством, порождается некоторой нормой. Так, на линейном пространстве можно определить дискретную метрику, расстояние сохраняется при сдвигах, но никакой нормой она не порождается.

Почти все примеры метрических пространств, рассмотренные ранее, в действительности являются линейными нормированными пространствами.

Полные линейные нормированные пространства называются банаховыми.

1. Конечномерные пространства .

Множество векторов является линейным пространством. Если определить норму вектора по формуле ||х||_р=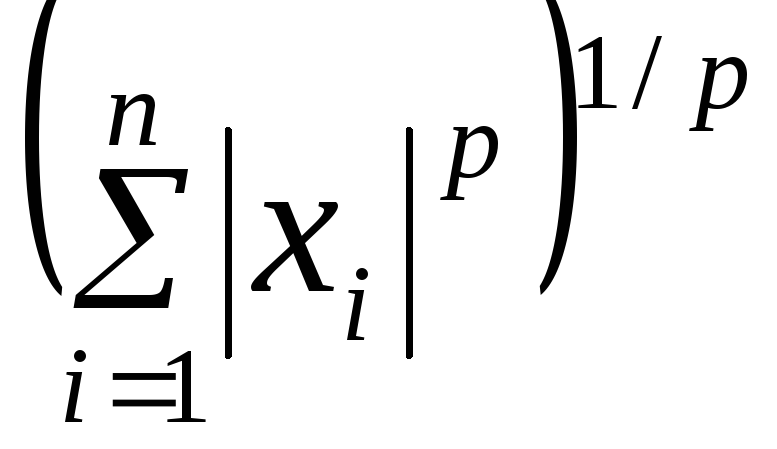(свойства нормы можно проверить с использованием неравенств Гельдера и Минковского), то расстояние, введенное ранее, порождается этой нормой. Аналогично для случаяр=: соответствующая норма имеет вид ||х||_=maxx_i. Все эти пространства полные, т.е. банаховы.

2. Пространство С.

Множество непрерывных функций на отрезке [0,1] является линейным пространством, поскольку функции можно складывать и умножать на скаляры (поточечно) c сохранением непрерывности и при этом справедливы аксиомы 1-8 из п. Error: Reference source not found. Если ввести норму по формуле ||х  y|| = max(х(t)), где максимум берется по всем значениям t, то метрика, порождаемая этой нормой, совпадает с метрикой из раннего. Тем самым, пространство С является линейным нормированным пространством. Поскольку это пространство полное, оно банахово.

3. Пространство m.

Сумма ограниченных последовательностей  ограниченная последовательность, ограниченность сохраняется и при умножении последовательности на число. Аксиомы линейного пространства легко проверяются. Тем самым, множество ограниченных последовательностей является линейным пространством. Если определить норму вектора ||х  y|| = max(х_i), то метрика в пространстве m порождается этой нормой. Пространство является банаховым.

Естественно, так же определяется норма и в пространстве сходящихся последовательностей с подпространстве m.

4. Пространство L^p_с.

Здесь норма, порождающая метрику из раннего, задается формулой ||х  y||_p=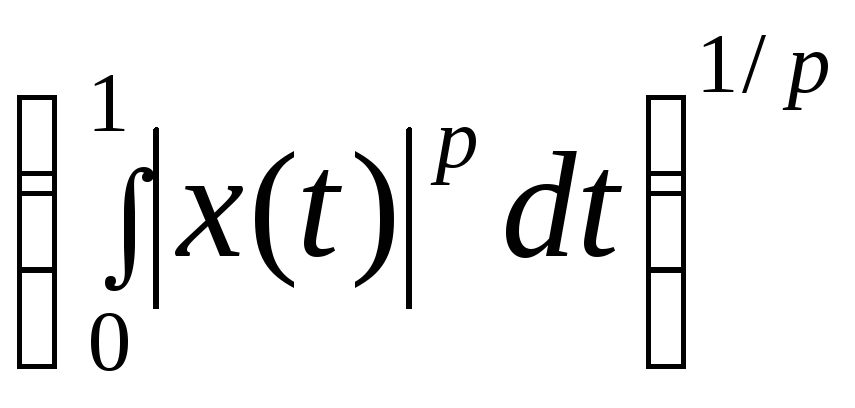. Пространство банаховым не является.

5. Пространство l^p.

Это пространство является линейным. Для этого сначала надо проверить, что сумма последовательностей из l^p также является элементом l^p. Норма в l^p определяется формулой ||х||=. Пространствоl^p банахово.

Проверим, что линейные операции и норма как функция на линейном нормированном пространстве непрерывны.

ПРЕДЛОЖЕНИЕ 11. Если х_nх, y_ny в пространстве Х и _n в пространстве R, то

х_n+y_nх+y;

_nх_nх;

||х_n||  ||х||.

Ограниченность множества в нашем случае согласно замечанию п. Error: Reference source not found равносильна тому, что множество содержится в некотором шаре с центром 0, т.е. ограниченности норм элементов множества. Шары в линейных нормированных пространствах обладают некоторыми дополнительными свойствами по сравнению с общими метрическими пространствами.

ПРЕДЛОЖЕНИЕ 12. Шары (замкнутые шары) в линейном нормированном пространстве являются выпуклыми множествами.

ПРЕДЛОЖЕНИЕ 13. Замыканием шара B(a,r) (r>0) является замкнутый шар (a,r). Заметим, что в общем случае метрических пространств это неверно.

ОПРЕДЕЛЕНИЕ 14. Замкнутое линейное многообразие в линейном нормированном пространстве называется линейным подпространством.

Позднее будет установлено, что конечномерные многообразия непременно являются подпространствами.

Например, в пространстве l¹ подпространством является множество S={xl¹:}.

Рассмотрим линейное многообразие в пространстве С, состоящее из непрерывно дифференцируемых функций. Линейность этого многообразия следует из правил дифференцирования. Многообразие не является подпространством, поскольку по теореме Вейерштрасса любую непрерывную функцию можно сколь угодно точно приблизить многочленом (это равносильно малости расстояния в метрике С), т.е. замыкание многообразия совпадает со всем пространством С. При этом в С существуют недифференцируемые функции (например, х1/2 ).

ТЕОРЕМА 6 (Ф.Рисс). Пусть L подпространство линейного нормированного пространства Х, не совпадающее со всем пространством. Для любого >0 существует вектор y такой, что 1 для всех хL.

Следует иметь в виду, что вектор со свойством может и не существовать. В важном частном случае гильбертова пространства такой вектор существует.