1. Замыкания множеств. Замкнутые и открытые множества.

ОПРЕДЕЛЕНИЕ 3. Пусть Х - метрическое пространство, М Х, аХ. Точка а называется предельной точкой М, если в любой окрестности а есть точки множества М\{a}. Последнее означает, что в любой окрестности а есть точки множества М, отличные от а.

Замечания. 1. Предельная точка может, как принадлежать, так и не принадлежать множеству. Например, 0 и 1 являются предельными точками множества (0,2), но первая ему не принадлежит, а вторая принадлежит.

2. Точка множества М может не являться его предельной точкой. В этом случае она называется изолированной точкой М. Например, 1  изолированная точка множества (1,0){1}.

3. Если предельная точка а не принадлежит множеству М, то найдется последовательность точек х_n M, сходящаяся к а в этом метрическом пространстве. Для доказательства достаточно взять открытые шары в этой точке радиусов 1/n и выбрать из каждого шара точку, принадлежащую М. Верно и обратное, если для а есть такая последовательность, то точка является предельной.

ОПРЕДЕЛЕНИЕ 4. Замыканием множества М называется объединение М с множеством его предельных точек. Обозначение .

Отметим, что замыкание шара не обязано совпадать с замкнутым шаром того же радиуса. Например, в дискретном пространстве замыкание шара B(a,1) равно самому шару (состоит из одной точки a) в то время как замкнутый шар (a,1) совпадает со всем пространством.

Опишем некоторые свойства замыкания множеств.

1. М. Это следует непосредственно из определения замыкания.

2. Если М  N, то . Действительно, еслиa ,a М, то в любой окрестности a есть точки множества М. Они же являются точками N. Поэтому a. Для точек изМ это ясно по определению.

3. .

4. .

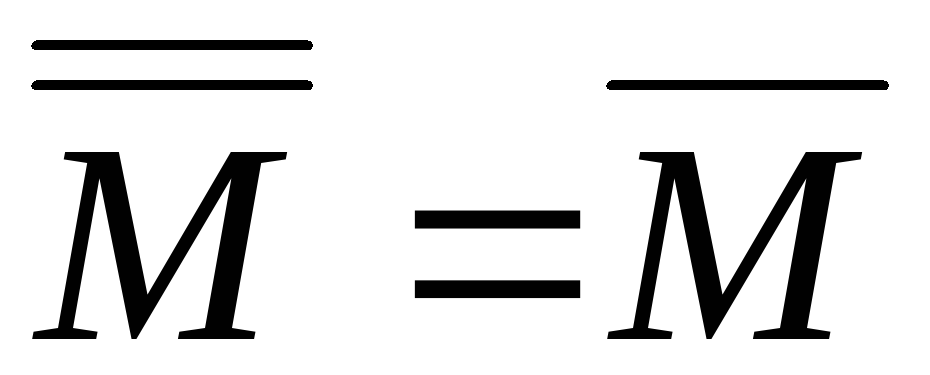5. Замыкание пустого множества пустое. Это соглашение не следует из общего определения, но является естественным.

ОПРЕДЕЛЕНИЕ 5. Множество M  X называется замкнутым, если ₌ M.

Множество M  X называется открытым, если замкнуто множество X\M.

Множество M  X называется всюду плотным в X, если ₌ X.

ОПРЕДЕЛЕНИЕ 6. Точка а называется внутренней точкой множества M, если B(a,r)M при некотором положительном r, т. е. внутренняя точка входит во множество вместе с некоторой окрестностью. Точка а называется внешней точкой множества M, если шар B(a,r)Х/M при некотором положительном r, т. е. внутренняя точка не входит во множество вместе с некоторой окрестностью. Точки, которые не являются ни внутренними, ни внешними точками множества M, называются граничными.

Таким образом, граничные точки характеризуются тем, что в каждой их окрестности есть точки как входящие, так и не входящие в M.

ПРЕДЛОЖЕНИЕ 4. Для того, чтобы множество являлось открытым, необходимо и достаточно, чтобы все его точки были внутренними.

Примерами замкнутых множеств на прямой являются [a,b], [a,). Открытых – (a,b), (a,). Множество [a,b) не открытое и не замкнутое (оно не содержит предельную точку b, а дополнительное множество не содержит предельную точку a). Все метрическое пространство Х и пустое множество  в силу соглашения 5 являются одновременно открытыми и замкнутыми. В дискретных метрических пространствах все подмножества одновременно открытые и замкнутые.

Из свойства 3 замыканий следует, что объединение двух (а тогда и любого конечного семейства) замкнутых множеств замкнуто. В то же время, объединение бесконечного семейства замкнутых множеств может и не быть замкнутым, например, = (0, 1).