
- •1.2.6 Термы
- •1.2.7 Формулы логики предикатов
- •1.2.8 Интерпретация и классификация формул логики предикатов.
- •1.2.9 Равносильные преобразования формул. Правила подстановки и эквивалентной замены
- •1.2.10 Предваренная нормальная форма
- •1.2.11 Сколемовская стандартная форма.
- •1. Следующие высказывания привести к пнф:
- •2. Привести высказывания к ссф:
1.2.9 Равносильные преобразования формул. Правила подстановки и эквивалентной замены
Определение 1. Две формулы,
и
![]() логики предикатов называются равносильными
на множестве М, если при
любой подстановке в эти формулы вместо
предикатных переменных любых конкретных
предикатов, определенных на М, формулы
превращаются в равносильные предикаты.
Если две формулы равносильны на любых
множествах, то их будем называть просто
равносильными. Равносильность
формул будем обозначать так:
логики предикатов называются равносильными
на множестве М, если при
любой подстановке в эти формулы вместо
предикатных переменных любых конкретных
предикатов, определенных на М, формулы
превращаются в равносильные предикаты.
Если две формулы равносильны на любых
множествах, то их будем называть просто
равносильными. Равносильность
формул будем обозначать так:
![]() .
.
Приведем пример двух неравносильных
формул логики предикатов. Покажем, что
![]() .
В самом деле, подставим вместо предикатных
переменных
.
В самом деле, подставим вместо предикатных
переменных
![]() и
и
![]() конкретные предикаты
конкретные предикаты
![]() и
и
![]() ,
определенные на множестве N. Тогда левая
формула превратится в высказывание
(нульместный предикат) «каждое натуральное
число либо нечетно, либо четно», которое
истинно. Правая формула превращается
в высказывание (нульместный предикат)
«либо каждое натуральное число четно,
либо каждое натуральное число нечетно»,
которое ложно.
,
определенные на множестве N. Тогда левая
формула превратится в высказывание
(нульместный предикат) «каждое натуральное
число либо нечетно, либо четно», которое
истинно. Правая формула превращается
в высказывание (нульместный предикат)
«либо каждое натуральное число четно,
либо каждое натуральное число нечетно»,
которое ложно.
Как и в алгебре высказываний, в логике предикатов можно заменять одну равносильную формулу другой. Переход от одной равносильной формулы к другой называется равносильным преобразованием исходной формулы. В процессе равносильных преобразований формул логики предикатов могут использоваться равносильности, известные из алгебры высказываний.
Правило подстановки.
Если в формуле
,
содержащей свободную переменную
![]() ,
выполнить всюду подстановку вместо
переменной
терма
,
выполнить всюду подстановку вместо
переменной
терма
![]() ,
то получим формулу
,
то получим формулу
![]() .
Этот факт записывают так:
.
Этот факт записывают так:
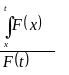
Подстановка называется правильной, если:
1) каждое вхождение переменной заменяется на один и тот же терм;
2) переменная не может быть заменена термом, содержащим ту же самую переменную.
Например,
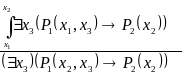
Это ‑ правильная подстановка, так как вместо свободной переменной можно подставить другую переменную.
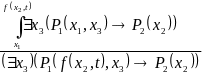
Это ‑ правильная подстановка, так как вместо свободной переменной можно подставить функцию.
Подстановка называется неправильной, если в результате подстановки свободная переменная окажется в области действия квантора или связанная переменная будет заменена термом.
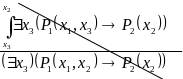
Это ‑ неправильная подстановка, так
как связанная переменная
![]() заменена свободной переменной
.
заменена свободной переменной
.
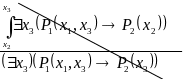
Это ‑ неправильная подстановка, так
как свободная переменной
заменяется связанной переменной
,
и предикат
![]() попадает в область действия квантора
попадает в область действия квантора
![]() .
.
Правило эквивалентной замены.
Если в формуле
![]() ,
содержащей вхождение некоторой формулы
,
содержащей вхождение некоторой формулы
![]() ,
хотим вместо формулы
подставить формулу
,
хотим вместо формулы
подставить формулу
![]() ,
причем
,
причем
![]() ,
то в формуле
не обязательно подставлять
во все вхождения формулы
,
можно заменить только некоторые вхождения
формулы
.
,
то в формуле
не обязательно подставлять
во все вхождения формулы
,
можно заменить только некоторые вхождения
формулы
.
Например, если в формулу
![]() хотим подставить вместо
эквивалентное выражение
хотим подставить вместо
эквивалентное выражение
![]() ,
то не обязательно в формуле заменять
все вхождения
эквивалентным выражением, можно заменить
только одно вхождение:
,
то не обязательно в формуле заменять
все вхождения
эквивалентным выражением, можно заменить
только одно вхождение:
![]() .
.
Пример. Упростить алгебраическое выражение:
![]() .
.
Решение. Выполним операцию отрицания:
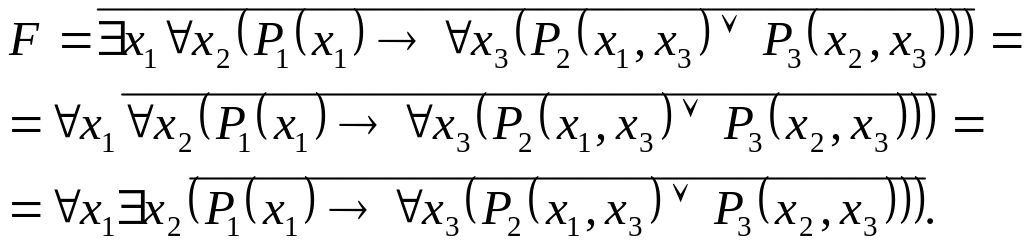
Удалим логическую связку « »:
![]()
Выполним операцию отрицания:
![]()
![]()
![]()
Переносим квантор влево:
![]()
