Закон мозлі

Закон Мозлі давав змогу визначати точні значення порядкових номерів елементів, а також передбачати положення ще не відкри­тих елементів у періодичній системі. Для цього треба знайти частоту лінії випромінюючого елемента, наприклад К_α, і порівняти її з графіком, одержаним для досліджених елементів (рис. 5.4). Старанні досліди Чедвіка (1920), який за розсіюванням α-частинок з великою точністю визна­чив заряди атомних ядер Купруму, Аргентуму, Платини, підтвердили, що вони збігаються з атомни­ми номерами у формулі Мозлі.

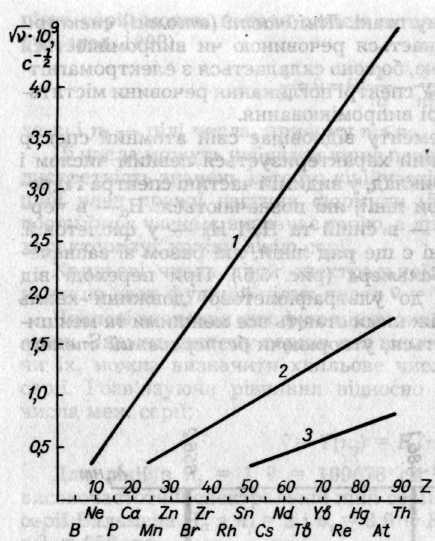
Рис. 5.4. Графік закону Мозлі: 1— лінія серії Кα; 2 — серії L_a; 3 — серії M_a

Приклад. Обчислити порядковий номер і назва­ти елемент, для якого до­вжина хвилі випроміню­вання К_а λ = 1,931 • 10 ^-8см. Відомо, що для К_а(Сu) λ = 1,541 • 10 ^-8 см.

Обчислюємо відповідні частоти обох елементів

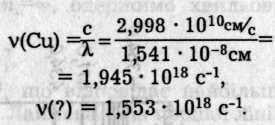
Визначаємо сталу а з рівняння Мозлі за спект­ральною лінією Купруму (v)^1/2= aZ, бо для К_а Ь = 1;

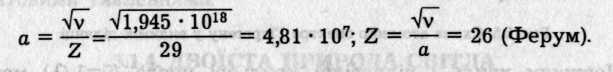
9 Квантово-механічна модель атома корпускулярно-хвильовий дуалізм

Двоїста природа світла наштовхнула де Бройля (1924) на думку про те, що корпускулярно-хвильовий дуалізм властивий будь-яким матеріальним частинкам. Для них повинно бути справед­ливим співвідношення

аналогічне для фотона, згідно з яким полю з довжиною хвилі λ відповідає частинка з масою т, яка рухається зі швидкістю v.

Гіпотезу де Бройля підтвердили досліди з дифракції електронів на монокристалі нікелю (Девіссон і Джермер, 1927), які дають таку ж дифракційну картину, як і рентгенівські промені: замість однієї плями виникають серії концентричних кілець різної інтенсивності. Дифракційні кільця спостерігали у тому ж році Дж. П. Томсон і Тартаковський при проходженні електронів крізь металеві плас­тинки. Була також виявлена (1930) двоїста природа а-частинок, маса яких у 7360 разів більша від маси електрона.

Хоч дуалізм властивий всім об'єктам матеріального світу, але виявляє себе тільки для мікрочастинок. Зокрема, з електроном, що

рухається зі швидкістю 2,2 • 10⁶ м/с, асоціюється довжина хвилі

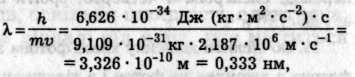
співмірна з розмірами атомів. Тому при проходженні електронів через кристали (дифракційну гратку) спостерігається їх диф­ракція. З рухом частинки, що має, наприклад, масу 1 г і швидкість руху 10 м/с, асоціюється хвиля довжиною лише

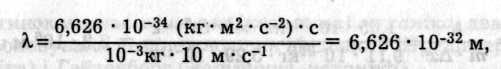
зафіксувати яку неможливо через відсутність відповідної дифрак­ційної ґратки. Це означає, що хвильові властивості макрооб'єктів не виявляються, якщо довжина хвилі значно менша, ніж розміри атома (10^-10 м).

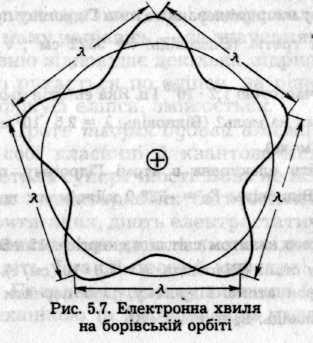
Обчислена з рівняння де Бройля довжина хвилі електрона (0,333 нм) дорівнює довжині кола першої борівської орбіти з радіу­сом а₀ = 0,053 нм. Таким чином, на стаціонарних орбітах довжина хвилі електрона повинна вкладатися ціле число разів (рис. 5.7), тобто

2πr=n λ

Отже, розмір квантово-механічної орбіти електрона кратний довжині його хвилі. Розв'язуючи рівняння разом з рівнянням де Бройля, приходимо до рівняння т vr = n

Принцип невизначеності

У хвильових властивостях електрона закладено перший прин­цип квантової механіки. Другим є принцип невизначеності (Гей-зенберг, 1927), згідно з яким неможливо одночасно точно визначити місце перебування мікрочастинки у просторі та її швидкість або імпульс. Добуток невизначеностей координати та швидкості (або імпульсу) мікрочастинки не може бути меншим від певного зна­чення

Δx *Δv≥/m, або Δx *Δр≥ (5.21)

Де Δх, Δv, Δр— невизначеності (похибки) у значеннях координати проекції швидкості та проекції імпульсу на вісь X у даний момент. Аналогічні співвідношення справедливі й для координат Y і Z.

Співвідношення невизначеностей зумовлене об'єктивними влас­тивостями мікрочастинок. Замкнена хвиля електрона охоплює атом, утворюючи електронну хмарку, в якій неможливо уявити рух електрона по певній траєкторії. Траєкторія розмивається, виникає смуга невизначеності, в межах якої перебуває електрон. Зі спів­відношення невизначеностей випливає, що чим точніше визначена область локалізації електрона (Δх→0), тим більша невизначеність його швидкості (Δv→) або імпульсу (Δр→), які з однаковою ймовірністю набувають будь-яких значень.

Обчислимо похибку у визначенні швидкості електрона в атомі Гідрогену, прийнявши невизначеність координати електрона рів­ною борівському радіусу. Підставивши у (5.21) значення радіуса та перетворивши вираз відносно Δv, одержимо

Оскільки похибка при обчисленні швидкості дорівнює швид­кості, то, фіксуючи координату електрона, не можемо визначити його швидкість.

Принцип невизначеності є загальним для всіх матеріальних об'єктів, але внаслідок малого значення для макрооб'єктів ним можна нехтувати.