11. Соотношение неопределенностей

Задача 11.1. Атом излучает фотон с длиной волны 800 нм. Известно, что время излучения t составляет 10^–8 с. С какой точностью может быть локализован фотон в направлении своего движения? Оценить относительную ошибку / в определении указанной длины волны, исходя из соотношения неопределенностей для энергии и времени.

Дано: λ = 800 нм = 8∙10-7 м Δt = 10–8 с

Δх – ? / – ?

Решение:

Т.к. точно неизвестно, в какой момент времени происходит излучение, то местонахождение фотона также невозможно точно определить. Если известен интервал времени, в котором происходит излучение, то положение фотона можно тоже определить лишь в некотором интервале координат:

Δx = c∙Δt,

где с = 3∙10⁸ м/с – скорость света (скорость распространения фотона).

Вычислим: Δx = 3∙10⁸∙10^–8 = 3 (м).

Чтобы найти /, воспользуемся соотношением неопределенностей для энергии и времени:

ΔЕ∙Δt ≥

или

,

где ħ =6,63∙10^-34Дж∙с – постоянная Планка.

Энергия фотона равна:

,

дифференцируя по λ, найдем dE:

.

Подставляя последнее выражение в соотношение неопределенностей, получим:

или

.

Отсюда найдем минимальную относительную ошибку в определении длины волны

.

Вычислим:

Ответ: м, .

Задача 11.2. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию протона, локализованного в области размером Δx = 10^-15м (размеры атомного ядра), пренебрегая релятивистскими эффектами.

Дано: Δx = 10-15м

Ekmin – ?

Решение:

Из соотношения неопределенностей координата–импульс

или

найдем

.

Кинетическая энергия протона в классическом случае равна .

Чтобы найти , надо найти производную от энергии по скорости:

,

отсюда

или .

Значит, .

Выразим :

.

Возьмем для оценки максимально возможное значение скорости с = 3∙10⁸ м/с, получим неопределенность в определении энергии частицы:

.

Минимальное значение кинетической энергии не может превышать эту неопределенность, поэтому

(Дж)

или

(эВ) или 200 МэВ.

Ответ: минимальная энергия частицы 200 МэВ.

12. Физика ядра

Задача 12.1. Вычислить удельную энергию связи ядра изотопа ₄Be⁸.

Решение:

При образовании ядра часть массы частиц, принимающих участие в этом процессе, идёт на создание энергии связи, которая определяется по формуле Эйнштейна

Есв = c2Δm,

(12.1)

где c – скорость света в вакууме, Δm – дефект масс, который находится как разность суммарной массы нуклонов и массы ядра:

Δm = [ZmР + (A – Z)mN] – mЯ .

(12.2)

где т_Р – масса протона; т_N – масса нейтрона; т_Я – масса ядра, Z – порядковый номер элемента в таблице Менделеева (он равен заряду ядра и, значит, числу протонов нем), А – массовое число (оно определяет количество нуклонов в ядре), соответственно, (A – Z) – число участвующих в образовании ядра нейтронов.

Удельная энергия связи – это энергия связи, приходящаяся на один нуклон, т.е.

(12.3)

В периодической таблице элементов (и в таблицах масс изотопов) приводятся массы атомов, а не ядер. Поэтому нужно учесть, что масса атома отличается от массы ядра на массу всех электронов, которых в атоме столько же, сколько протонов в ядре (это обеспечивает электрическую нейтральность атома). Поэтому массу ядра можно найти так:

mЯ = mА – Z mе.

(12.4)

Подставим (12.4) в формулу для дефекта масс (12.2) и перегруппируем слагаемые:

Δm = [Zm_Р + (A – Z)m_N] – [m_А – Z m_е] =Z (m_Р + +m_е) + (A – Z)m_N – m_А

Δm = Z m (1Н1) + (A – Z)mN – mА.

(12.5)

Здесь мы обозначили m (₁Н¹) = m_Р + m_е – масса атома водорода, которую также, как и массу рассматриваемого изотопа, возьмем из таблицы.

Теперь выпишем все необходимые данные из таблиц:

m_Р = 1,00728 а.е.м.;

mN = 1,00867 а.е.м.;

m (₁Н¹) = 1,00783 а.е.м.;

mА = m (₄Be⁸) = 8,00531 а.е.м.;

1 а.е.м. = 1,6605655·10-27 кг;

c = 2,9979·10⁸ м/с.

Для изотопа бериллия ₄Be⁸ определяем, что Z = 4, A = 8.

Подставляем все эти данные в выражение для дефекта масс (12.5):

Δm = 4· 1,00783 + 4·1,00867 – 8,00531 = 0,06069 (а.е.м.)

Переведем полученное значение в килограммы:

Δm = 0,06069 · 1,6605655·10^-27 = 0,10078·10^-27 = 1,0078·10^-28 (кг).

Теперь вычислим энергию связи по (13.1):

Е_св =(2,9979·10⁸ )²· 1,0078·10^-28 = 9,0575·10^–12 (Дж)

Переведем полученное значение в электрон-вольты:

1 эВ = 1,6·10^–19 Дж

Е_св = = 5,66·10⁷ (эВ) или Е_св =56,6 МэВ.

Тогда, согласно (12.3), на один нуклон в ядре приходится энергия

МэВ.

Ответ: удельная энергия связи ядра изотопа бериллия ₄Be⁸ равна 7,08 МэВ.

Задача 12.2. Определить возраст древних деревянных предметов, если известно, что удельная активность изотопа С¹⁴ у них составляет 3/5 удельной активности этого изотопа в только что срубленных деревьях. Период полураспада ядер С¹⁴ равен 5570 лет.

Дано: T = 5570 лет

t – ?

Решение:

Известно, что деревья поглощают углекислый газ, преобразуя его в углерод и кислород. В состав углекислого газа (СО₂) помимо углерода С¹² в небольшом количестве входит изотоп С¹⁴. Когда дерево срубают, оно перестает поглощать СО₂, и количество углерода в нем больше не увеличивается. Изотоп углерода С¹⁴ радиоактивен, и со временем его количество уменьшается в результате распада. По оставшемуся количеству С¹⁴ в деревянных изделиях определяют их возраст.

Активность изотопа определяет количество распадающихся ядер в единицу времени:

или ,

где N – количество наличных ядер, – постоянная распада, Т – период полураспада.

Удельная активность – это активность единицы массы изделия, т.е.

,

а в только что срубленных деревьях

.

Запишем закон распада в интегральном виде (предполагая, что возраст деревянных изделий соизмерим с периодом полураспада):

или

,

где N – количество наличных ядер, N₀ – исходное количество ядер.

Левую часть этого равенства, пренебрегая изменением массы деревянного изделия, можно заменить на отношение удельных активностей:

или

.

Потенцируя последнее выражение, находим время t , за которое произошло такое уменьшение активности, – возраст деревянных предметов:

.

Вычислим:

(лет).

Ответ: деревянным предметам 4107 лет.

Задача 12.3. В урановой руде обнаружен ₈₂Рb²⁰⁶. Чему равен возраст урановой руды, если она теперь содержит 0,8 г свинца на каждый грамм ₉₂U²³⁸?

Дано: m(92U238) = 1 г = 10–3 кг m(82Pb206) = 0,8 г = 0,8∙10–3 кг

t – ?

Решение:

Каждое ядро атома свинца образуется из ядра атома урана в результате нескольких ядерных реакций распада. Уран, содержащийся в руде, распадается все время существования руды, при этом количество урана в руде уменьшается, а количество свинца растет. В некоторый момент времени t на N ядер урана приходится ΔN ядер свинца, т.е. распавшихся ядер урана. Распишем число ядер через массу (считаем, что масса ядра практически равна массе атома):

, .

Полагая, что возраст урановой руды соизмерим с периодом полураспада урана, запишем закон распада в интегральном виде:

,

где N – количество наличных ядер, N₀ – исходное количество ядер, – постоянная распада, Т – период полураспада урана (из справочной таблицы Т(₉₂U²³⁸) = 4,5∙10⁹ лет).

Исходное количество ядер N₀ = N + ΔN, тогда закон распада примет вид:

или

.

Потенцируя последнее выражение, получаем:

или

.

Подставим выражения для N и ΔN и выразим время:

.

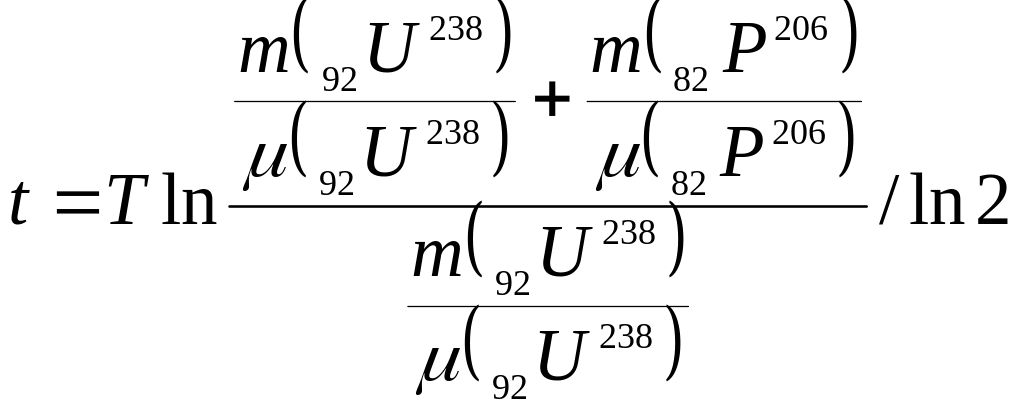Молярные массы урана и свинца равны:

μ (₉₂U²³⁸) = 0,238 кг/моль, μ (₈₂Pb²⁰⁶) = 0,206 кг/моль.

Вычисление:

(лет).

Ответ: возраст урановой руды составляет 4,25∙10⁹ лет.