
- •2)Ускорение точки. Нормальное и тангенсальное кскорение. Проекции ускорения на координатные оси.
- •3) Кинематика вращательного движения. Угловая скорость и ускорение.
- •4)Динамика мат. Т-ки. Сила,масса и импульс частицы. З-ны Ньютона.
- •5) Инерциальные системы отсчета. Принцип относительности Галилея. Преобразования Галилея.
- •7)Центр инерции (масс). Движение центра инерции замкнутой с-мы.
- •8) Работа. Работа переменной силы. Мощность.
- •11)Полная механическая энергия системы. З-н сохранения механической энергии.
- •12) Вращательноe движение твердого тела. Момент инерции мат т-ки и тв тела относительно неподвижной оси. Кинетическая энергия вращающегося тв тела. Т-ма Штейнера.
- •13)Работа, совершаемая при вращении тв тела. Момент силы от-но точки и оси вращения. Осн ур-е динамики вращательного двожения тв тела.
- •14)Момент импульса мат т-ки и тв тела от-но неподвижной оси вращения. З-н сохранения импульса.
- •15)Понятие о неинерциальных системах отсчета и силах инерции
- •Скорости газовых молекул. Закон Максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная ,средняя квадратичная и средняя арифметическая скорости молекул.
- •Барометрическая формула. Распределение молекул в поле силы тяжести. Распределение Больцмана.
- •Среднее число столкновений и средняя длина свободного пробега молекул. Зависимость средней длины свободного пробега молекул от давления и температуры.
- •Явления переноса в газах.З-ны диффузии, внут трения и теплопроводности.
- •23, Число степеней свободы молекул. З-н равномерного распространения энергии по степеням свободы молекул. Внут энергия ид газа
- •Теплоемкость. Зависимость теплоемкости ид газа от вида процесса. Классическая теория теполемкости ид газа и ее ограниченность.
- •Первое начало термодинамики и изопроцессы.
- •Первое начало термодинамики и адиабатический процесс.Политропический процесс.
- •Реальные газы. Силы и потенц энергия межмолекулярного воздействия.Ур-е Ван-дер-Ваальсса.
- •Поверхностный слой жидкости.Поверхностное натяжение.Коэф пов нат и его зависимость от т-ры и примесей пав.
- •32. Явление смачивания.Краевой угол.Св-ва тонких пленок.
- •31. Давление под ихогнутой пов-тью жтдкости.Ф-ла Лапласа. Капиллярные давления.
Скорости газовых молекул. Закон Максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная ,средняя квадратичная и средняя арифметическая скорости молекул.
Eпост=(m0Vкв)\2=3\2кТ;
Vкв=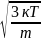 =
= В молекулярном пучке имеются молекулы
со всевозможными скоростями, как с
маленькими так и с очень большими.
Несмотря на полную хаотичность движения
газ молекул и случайный хар-р столкновения
их м\у собой распределение их по скоростям
является не случайным,а вполне
определенным. В состоянии т\д равновесия
распределение молекул данного газа по
скоростям является однозначным и
единственно возможным,молекулы равномерно
распределяются по направлениям скоростей
и импульсов и статически по значениям
скоростей и импульсов.
В молекулярном пучке имеются молекулы
со всевозможными скоростями, как с
маленькими так и с очень большими.
Несмотря на полную хаотичность движения
газ молекул и случайный хар-р столкновения
их м\у собой распределение их по скоростям
является не случайным,а вполне
определенным. В состоянии т\д равновесия
распределение молекул данного газа по
скоростям является однозначным и
единственно возможным,молекулы равномерно
распределяются по направлениям скоростей
и импульсов и статически по значениям
скоростей и импульсов.
Закон распределения молекул идеального газа по скоростям (закон Максвелла) определяет вероятное количество dN молекул из полного их числа N (число Авогадро) в данной массе газа, которые имеют при данной температуре Т скорости, заключенные в интервале от V до V + dV: dN/N=F(V)dV F(V) - функция распределения вероятности молекул газа по скоростям определяется по формуле; F(V)=4π(M/2πRT)3/2 V2 exp(MV2/2RT) где V - модуль скорости молекул, м/с; - абсолютная температура, К;М - молярная масса, кг/моль.R = 8,3144 Дж/(моль•К) - универсальная газовая постоянная в системе СИ.
VB=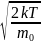 =
=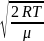 ;
V=
;
V=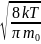 =
=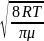 ;
Vкв=
=
;
Vкв=
=
Барометрическая формула. Распределение молекул в поле силы тяжести. Распределение Больцмана.
Если бы молекулы газа не двигались хаотически, то под действием поля тяжести они бы скатились по поверхности земли. Если бы отсутствовало поле тяжести земли, то за счет хаотического движения молекулы газа разлетелись бы по мировому пространству. За счет действия 2ч противоположных процессов в газах устанавливается динамическое равновесие.В результате чего давление зем атмосферы с высотой будет убывать
При dh>0, dP<0,dp=--ρgdh, ρ=μgp\rt.
P=p0 = p0
= p0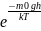 с увеличением высоты давление ид газа
убывает по
с увеличением высоты давление ид газа
убывает по
Р=nkT; p0=n0kT;концентрация молекул зависит от их потенц энергии,чем >конц тем <энергия.
Применительно к зем втмосфере с увеличением высоты следовало бы ожидать расслоение атм на отдельные компоненты. Опыты показывают что этого не происходит. g↓ с увеличением h,T↓
Больцман вывел з-н по равномерному распределению энергии движения по мтепени=ям свободы молекул: для статистической системы в состоянии т\д равновесия на каждую степень поступ и вращательного движения в среднем приходится энергия тепового движения равная 1\2кТ, а на каждую степень колеб дв-я кТ.
Среднее число столкновений и средняя длина свободного пробега молекул. Зависимость средней длины свободного пробега молекул от давления и температуры.
м\у 2мя последовательными сталкновениями солекулы движутся прямолинейно и равномерно и проходят путь наз длиной свободного пробега. Длина свободного пробега является случайной статической величиной,поэтому вводят величину наз средняя длина свободного пробег- расстояние к-е проходят большинство молекул м\у 2мя последовательными сталкновениями при данных усл.
λ=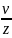 ,
где z-число
столкновений, z=nπd2𝓋
если учесть движения всех молекул z=
,
где z-число
столкновений, z=nπd2𝓋
если учесть движения всех молекул z=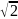 nπd2𝓋,
тогда λ=
nπd2𝓋,
тогда λ=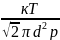 .
Λзависит от : 1) если р=const,
то наблюдается малая зависимость от
т-ры,с повыш т-ры d↓
2)если Т= const,
то λ~
.
Λзависит от : 1) если р=const,
то наблюдается малая зависимость от
т-ры,с повыш т-ры d↓
2)если Т= const,
то λ~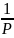 .
С увеличением Р уменьшается расстояние.
.
С увеличением Р уменьшается расстояние.
