Алгоритм построения минимального остовного дерева.
Алгоритм построения минимального остовного дерева предполагает соединение
всех узлов сети с помощью путей наименьшей длины. Типичной задачей, для решения которой необходим такой алгоритм, является создание (проектирование) сети
дорог с твердым покрытием, соединяющих населенные пункты в сельской местности,
где дороги, соединяющие два каких-либо пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект дорожной системы должен минимизировать общую длину дорог с твердым покрытием, при этом желаемый результат
можно получить с помощью алгоритма построения минимального остовного дерева.
Опишем процедуру выполнения этого алгоритма. Обозначим через N = {1, 2, ..., п)
множество узлов сети и введем новые обозначения:
С4 — множество узлов сети, соединенных алгоритмом после выполнения k-й
итерации этого алгоритма,
Ск — множество узлов сети, не соединенных с узлами множества Ch после выполнения k-й итерации этого алгоритма.
Этап 0. Пусть Со = 0 и Со = N.
Этап 1. Выбираем любой узел i из множества Со и определяем С, = {i}, тогда С, = N - {i}. Полагаем k — 2.
Основной этап к. В множестве Ск_, выбираем узел/, который соединен самой
короткой дугой с каким-либо узлом из множества Ct_,. Узел / при-
соединяется к множеству С^ и удаляется из множества Ct_,. Та-
ким образом, С, = Ск_, + {/}, Ct = Ct_, - {/}.
Если множество Ск пусто, то выполнение алгоритма заканчивается.
В противном случае полагаем k — k + 1 и повторяем последний этап.
Алгоритм Дейкстры.
В процессе выполнения этого алгоритма при переходе от
узла i к следующему узлу / используется специальная процедура пометки ребер.
Обозначим через и, кратчайшее расстояние от исходного узла 1 до узла i, через dtj —
длину ребра (г, j). Тогда для узла у определим метку [uJt i] следующим образом.
[uj,i] = [ul + dli,i],dli>0
Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную,
если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус
временной метки изменяется на постоянный.
Вычислительная схема алгоритма состоит из следующих этапов.
Этап 0. Исходному узлу (узел 1) присваивается постоянная метка [0, —].
Полагаем i = 1.
Этап 1.
а) Вычисляются временные метки [и: + dtj, t] для всех узлов у, которые можно
достичь непосредственно из узла i и которые не имеют постоянных ме-
256
Глава 6. Сетевые модели
ток. Если узел j уже имеет метку [uy, k], полученную от другого узла k, и,
если и, + dtj < ujt тогда метка [и., k] заменяется на [u, + dljt i].
b) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [ur, s] с наименьшим значением расстояния иг среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = г и повторяем этап i.
Алгоритм Флойда.
Этот алгоритм более общий по сравнению с алгоритмом
Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами
сети. В этом алгоритме сеть представлена в виде квадратной матрицы с п строками и п столбцами. Элемент (?, у) равен расстоянию dtj от узла i к узлу j, кото-
рое имеет конечное значение, если существует дуга (i, j), и равен бесконечности
в противном случае.
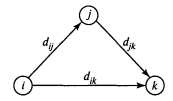
Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k
и заданы расстояния между ними (рис. 6.19). Если выполняется неравенство
dll + djh<dtk, то целесообразно заменить путь i->fe путем i->j->k. Такая замена
(далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.
Алгоритм Флойда требует выполнения следующих действий.
Этап 0. Определяем начальную матрицу расстояний Do и матрицу последовательности узлов So. Диагональные элементы обеих матриц
помечаются знаком "—", показывающим, что эти элементы в вычислениях не участвуют. Полагаем к = 1.
Основной этап к. Задаем строку k и столбец k как ведущую строку и ведущий
столбец. Рассматриваем возможность применения треугольного
оператора ко всем элементам dtj матрицы Dk^. Если выполняется
неравенство
dtk + dkj < dtj, (i*k,j*kui*j),
то делаем следующее:
a) создаем матрицу Dk путем замены в матрице Dk_1 элемента dl}
суммой dlk + dhj,
b) создаем матрицу Sk, меняя в матрице S4_j элемент st/ на k. Пола-
гаем k — k + lu повторяем этап k.
Поясним действия, выполняемые на k-м этапе алгоритма, представив матрицу
Dk_l так, как она показана на рис. 6.20. На этом рисунке строка k и столбец k являются ведущими. Строка i — любая строка с номером от 1 до k - 1, а строка р —
произвольная строка с номером от k + 1 до п. Аналогично столбец j представляет
любой столбец с номером от 1 до k - 1, а столбец q — произвольный столбец с номе-
ром от k + 1 до п. Треугольный оператор выполняется следующим образом. Если
сумма элементов ведущих строки и столбца (показанных в квадратиках) меньше
элементов, находящихся на пересечении столбца и строки (показаны в кружках),
соответствующих рассматриваемым ведущим элементам, то расстояние (элемент
в кружке) заменяется суммой расстояний, представленных ведущими элементами.
После реализации п этапов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам.
1. Расстояние между узлами i и у равно элементу dtj в матрице Dn.
2. Промежуточные узлы пути от узла i к узлу j определяем по матрице Sn.
Пусть s0 = k, тогда имеем путь i -» k -» j. Если далее slk = k и shi = j, тогда
считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла
i к узлу k и от узла k к узлу у.
Целочисленное программирование.
Целочисленное линейное программирование (ЦЛП) ориентировано на решение
задач линейного программирования, в которых все или некоторые переменные
должны принимать целочисленные (или дискретные) значения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На
сегодня не существует надежных вычислительных алгоритмов решения таких задач.