6. После установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии).

Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще всего используются следующие типы функций:

• линейная — ;

• гиперболическая — ;

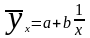• параболическая — ;

• показательная — .

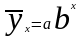Для проверки возможности использования линейной функции определяется разность ( ); если она менее 0,1, то считается возможным применение линейной функции. Для решения этой же задачи можно использовать величину , определяемую по формуле

, (7.22)

где m — число групп, на которое разделен диапазон значений факторного признака.

Если окажется меньше табличного значения F-критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается. Значение F -критерия определяется по таблице в зависимости от уровня значимости = 0,05 (вероятность Р = 0,95) и числа степеней свободы числителя ( ) и знаменателя ( ) (см. приложение 5).

Построение уравнения парной регрессии

При линейной связи параметры уравнения парной регрессии:

(7.23) находятся из системы уравнений:

, (7.24)

которая получается применением метода наименьших квадратов. Из первого уравнения системы (7,24) следует, что:

. (7.25)

Подставив полученное выражение во второе уравнение, получим:

. (7.26)

Коэффициент корреляции определяется по формуле:

(7.27)

Учитывая (7,26) и (7,27) получим

(7.28)

или . (7.29)

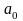Зная значения r, и можно вычислить по выражениям (7.29) и (7.25) параметры и линейного уравнения регрессии, а также значение среднего коэффициента эластичности:

(7.30)

Статистический анализ модели

Оценка параметров парной регрессии выполняется исходя из следующих предпосылок . Допустим, что в генеральной совокупности связь между x и y линейна. Наличие случайных отклонений, вызванных воздействием на переменную y множества других, неучтенных в уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин и приобретает вид:

(7.31)

Здесь - случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений , то можно было бы рассчитать значения параметров и . Так как они неизвестны, то по наблюдениям и можно получить только оценки параметров и , которые сами являются случайными величинами в связи с тем, что соответствуют случайной выборке. Пусть 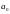- оценка параметра , - оценка параметра . Тогда оцененное уравнение регрессии будет иметь вид:

(7.32)

Для того чтобы оценки и обладали адекватностью ряд остатков

(7.33)

должен удовлетворять следующим требованиям:

1. математическое ожидание равно нулю (критерий нулевого среднего);

2. величина является случайной переменной (критерий серий);

3. значения независимы между собой (критерий Дарбина-Уотсона);

4. дисперсия постоянна: для всех i, j (тест Гольдфельда-Квандта);

5. Остатки распределены по нормальному закону (свойство используется для проверки статистической значимости и построения доверительных интервалов при прогнозировании)

Известно, что если данные условия выполняются, то оценки, сделанные с помощью метода наименьших квадратов, обладают следующими свойствами:

- оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению:

Это вытекает из того, что и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии;

- оценки состоятельны, т.к. дисперсии оценок параметров при возрастании числа наблюдений стремятся к нулю: ; 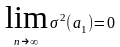т.е. надежность оценки при увеличении выборки растёт;

- оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра.

Если предположения 3 и 4 нарушены, т.е. дисперсия возмущений непостоянна или значения связаны друг с другом, то свойства несмещенности и состоятельности сохраняется, но свойства эффективности – нет.

Отметим, что аппроксимировать уравнением парной регрессии у на х, имеет смысл только в том случае, если существует достаточно тесная статистическая зависимость между случайными величинами и линейный коэффициент корреляции является значимым, что и имеет место в рассматриваемом примере.

Оценка качества построенной модели

Формально качество модели определяется ее адекватностью и точностью. Эти свойства исследуются на основе анализа ряда остатков (отклонений расчетных значений от фактических):

При этом адекватность является более важной составляющей качества, но сначала рассмотрим характеристики точности и нормальности ряда остатков, так как некоторые из них используются при расчете различных критериев адекватности.

Характеристики точности

Под точностью понимается величина случайных ошибок. Сравнительный анализ точности имеет смысл только для адекватных моделей: среди них лучшей признается модель с меньшими значениями характеристик точности, к которым относятся:

- максимальная ошибка соответствует максимальному отклонению расчетных значений от фактических;

- средняя абсолютная ошибка

показывает, насколько в среднем отклоняются фактические значения от модели;

- остаточная дисперсия

;

- средняя квадратическая ошибка

. (7.34)

Средняя квадратическая ошибка является наиболее часто используемой характеристикой точности (что объясняется ее связью с остаточной дисперсией, которая играет центральную роль в регрессионном анализе). Значение средней квадратической ошибки всегда несколько больше значения средней абсолютной ошибки, но они имеют схожий смысл – характеризуют среднюю удаленность расчетных значений модели от фактических исходных данных. Обычно точность модели признается удовлетворительной если выполняется условие:

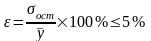. (7.35)

К характеристикам точности можно отнести также множественный коэффициент детерминации

, (7.36)

характеризующий долю дисперсии зависимой переменной, объясненной с помощью регрессии, и множественный коэффициент корреляции (индекс корреляции):

. (7.37)

В случае парной линейной регрессии значение множественного коэффициента корреляции совпадает с линейным коэффициентом корреляции.

Проверка нормальности ряда остатков может быть выполнена приближенно по условиям (7.2). В связи с тем, что каждый из относительных показателей формы распределения меньше 1,5 эмпирическое распределение ряда остатков не противоречит нормальному.