Выражение напряжений через изгибающие и крутящие моменты

Сравнивая выражения напряжений и моментов через прогибы плиты, получаем формулы для вычисления напряжений через моменты

(20)

Нормальные напряжения . и касательные напряжения от кручения плиты меняются по толщине плиты по линейному закону. Эпюры распределения напряжений по толщине плиты приведена на рисунке 28. Максимальные значения этих напряжений определяются формулами

(21)

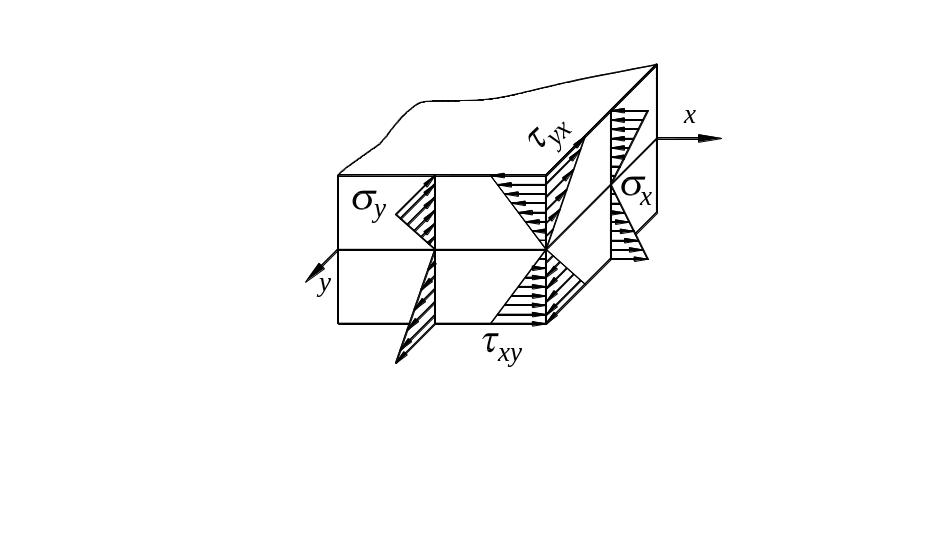
Рисунок 28

Выражение поперечных сил через прогибы плиты

Используя первые два дифференциальных уравнения равновесия плит (8), из первого получим

(22)

Аналогично из второго дифференциального уравнения равновесия (8) получаем выражение для поперечной силы

(23)

Основное уравнение изгиба плит

Подстановка поперечных сил в третье дифференциальное уравнение равновесия (8) связывает прогибы с внешней нагрузкой

После изменения знаков и деления на цилиндрическую жесткость окончательно получаем основное уравнение изгиба плит

(24)

Это уравнение носит название уравнения Софи Жермен и Лагранжа. Оно может быть записано в развернутом виде

(24-а)

или в сокращенных видах

, (24-б,в)

В выражениях (24-б.в) введен оператор Лапласа

(25)

Постановка задачи

В плитах перемещения, деформации, напряжения и все внутренние усилия выражаются через прогибы. Поэтому решить плиту значит найти функцию прогибов, которая отвечает основному уравнению изгиба плит и граничным условиям или условиям опирания плиты

Определение опорных реакций плит

Основное уравнение изгиба плит является уравнением четвертого порядка, поэтому оно позволяет учесть на каждой опорной кромке плиты только по 2 граничных условия, а имеем на границе плиты три внутренних усилия. Так на краю плиты, нормалью к которому является ось , действуют и (Рис. 29-а).

Рисунок 29

На элемент границы плиты длиной действует крутящий момент , а на другой такой же элемент, отстоящий от рассматриваемого на , действует крутящий момент величиной (Рис. 29-b). Причем, крутящий момент образуется горизонтальными касательными напряжениями (Рис. 29-с). Учитывая, что высота плиты мала по сравнению с габаритными размерами, крутящий момент по принципу Сен-Венана можно заменить эквивалентной парой сил. Кирхгоф предложил заменить горизонтальную пару вертикальной парой сил (Рис. 30-а). Такое изменение будет влиять на напряженное состояние только возле кромки плиты. Такая замена дает на элемент длиной добавку к опорной реакции, равную . При этом на единицу длины приходится . Следовательно, общая реакция составляет

(27)

Аналогично записывается реакция на кромке плиты, нормалью к которой является ось

(28)

В каждом углу плиты возникает реактивная сосредоточенная сила, стремящаяся поднять углы вверх и равная

(29)

Подставляя выражения изгибающих и крутящих моменьов через прогибы плиты в реакции (27) и (28), получим

,

Примерное распределение опорных реакций для прямоугольной плиты показано на рисунке 31

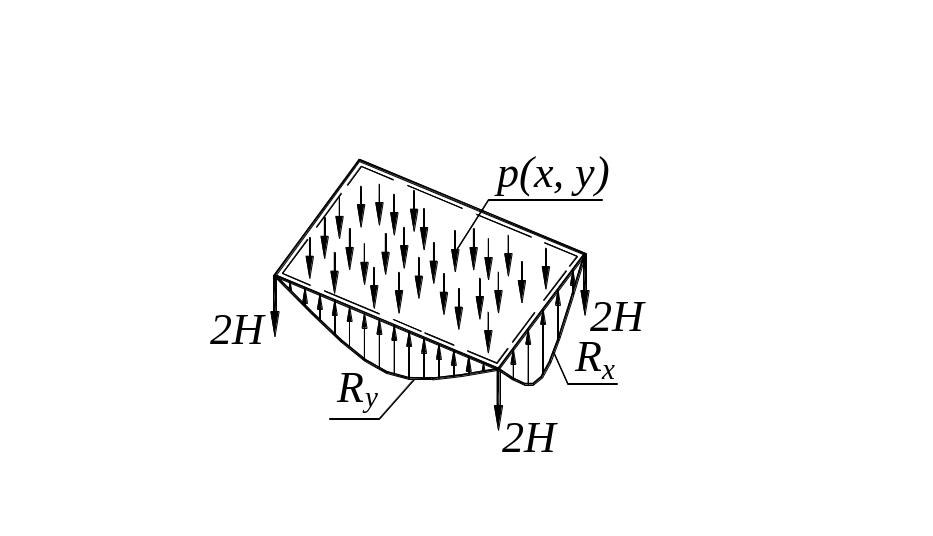
Рисунок 31

Формулировка граничных условий в плитах

Функция прогиба в задаче изгиба плит должна удовлетворять основному уравнению изгиба плит и граничным условиям, описывающим характер опирания плиты на каждой ее кромке. Пусть имеем плиту прямоугольную в плане, у которой одна грань жестко защемлена, другая грань шарнирно опирается, а две остальные грани свободны (Рис. 32).

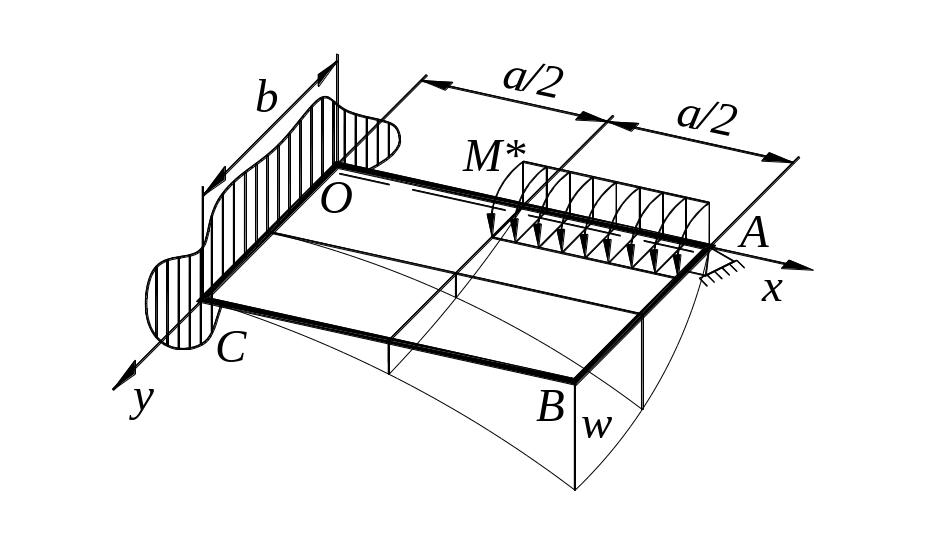
Рисунок 32.

Рассмотрим условия на каждой грани. Грань ОС ( ) жестко закреплена, поэтому на ней невозможны ни вертикальное перемещение, ни поворот опорного сечения , . Грань ОА ( ) шарнирно оперта, т.е. прогиб равен нулю и известен изгибающий момент , который или равен нулю (если на опоре нет моментной нагрузки), или равен приложенной моментной нагрузке. Для случая приведенного на рисунке 32 эти условия записываются так , Для формулировки граничных условий на прогибы последнее выражение с учетом того, что грань прямолинейна, т.е. , принимает вид Грань АВ представляет собой свободный край. На этой грани неизветны и прогиб и угол поворота, но известны изгибающий момент и ветикальная составляющая внутренних усилий, т.е. , если нет на кромке моментной нагрузки, (или равен распределенной по кромке моментной нагрузке), и , если нет распределенной по кромке вертикальной нагрузки (или равна распределенной вертикальной нагрузке). Через прогибы эти уловия записываются следующим образом

,

Условия на грани СВ формулируются аналогично грани АВ только для изгибающего момента и вертикальной составляющей внутренних сил .

На этом теоретическая часть технической теории изгиба плит закончена; остальное это методы интегрирования основного уранения изгиба плит.