5.2.1. Движение системы. Центр инерции

Если система не замкнута, то записав уравнения движения для каждой материальной точки системы, сложив их и учтя, что векторная сумма внутренних тел равна нулю, придем к уравнению

(5.1)

где – импульс системы n материальных точек, F – векторная сумма всех внешних сил, действующих на точки системы. Таким образом, скорость изменения импульса системы материальных точек равна результирующей всех внешних сил, действующих на точки системы, и направлена вдоль этой результирующей силы.

Уравнение (5.1) является обобщением соответствующего уравнения для одной материальной точки и называется уравнением движения системы. Умножив это уравнение на dt, и проинтегрировав обе части полученного равенства по времени между моментами t₁ и t₂, придем к теореме об изменении импульса системы:

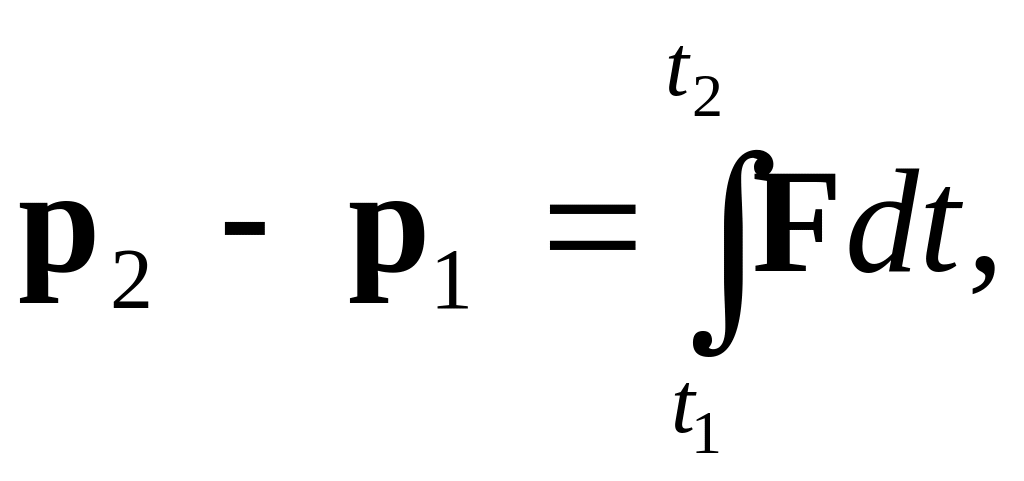
аналогичное соответствующей теореме для одной материальной точки. Здесь p₁ и p₂ – импульсы системы в моменты времени t₁ и t₂. Следовательно, изменение импульса системы материальных точек за промежуток времени от t₁ до t₂ равно импульсу всех внешних сил, действующих на точки системы за этот промежуток времени. Теорему об изменении импульса можно рассматривать как более общую формулировку закона сохранения импульса системы, так как в ней указана причина изменения импульса – действие других тел (посредством внешних сил F).

В любой системе материальных точек имеется одна замечательная геометрическая точка С, называемая центром инерции или центром масс системы. Ее положение в заданной системе координат определяется радиус-вектором

(5.2)

где – масса системы, r_i – радиус-вектор i-ой материальной точки. Декартовы координаты центра инерции системы определятся так:

(5.3)

В случае однородного поля сил тяжести центр инерции совпадает с центром тяжести, т.е. с точкой приложения силы тяжести, являющейся равнодействующей параллельных сил, приложенных к материальным точкам в однородном поле силы тяжести.

Продифференцировав выражение (5.2) по времени, найдем скорость движения центра инерции:

(5.4)

где – импульс системы. Откуда,

p = mv_C. (5.5)

Следовательно, импульс системы материальных точек можно определить как произведение массы системы на скорость движения ее центра инерции.

Если система замкнута, то p = const, а значит, v_С = const. Следовтельно, центр инерции замкнутой системы движется равномерно и прямолинейно, в частности, он может покоится. Этот вывод есть обобщение закона инерции и понятия покоя на случай системы материальных точек. Скорость v_С имеет смысл скорости движения системы как целого. Если система замкнута и ее центр инерции вначале покоился (v_С = 0) или двигался равномерно и прямолинейно, то никакие движения точек системы под действием внутренних сил не изменят этого состояния центра инерции. Это – так называемый закон сохранения центра инерции.

Если система не замкнута, то импульс системы будет изменяться со временем. Продифференцировав соотношение (5.5) и учтя, что где F – результирующая всех внешних сил, действующих на систему, получим

ma_C = F, (5.6)

где a_C = dv_C/dt – ускорение центра инерции системы. Уравнение (5.6) выражает собой, так называемую теорему о движении центра инерции: произведение массы системы на ускорение ее центра инерции равно геометрической сумме всех действующих на систему внешних сил. Сравнивая это уравнение с уравнением второго основного уравнения динамики материальной точки, можно дать другую формулировку этой теоремы: центр инерции системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Эта теорема объясняет, почему поступательно движущееся тело можно рассматривать как материальную точку с массой, равной массе тела и оправдывает введение самого понятия материальной точки. Практическое значение этой теоремы состоит в том, что она позволяет при определении закона движения центра масс любой системы исключить из рассмотрения все наперед неизвестные внутренние силы. Другими словами, она позволяет свести движение системы к движению одной материальной точки.

5.2.2. Реактивное движение. Формула Циолковского

Закон сохранения импульса как один из фундаментальных законов природы проявляется в целом ряде явлений. В частности, он лежит в основе реактивного движения. Используя этот закон, найдем зависимость скорости ракеты от изменения ее массы.

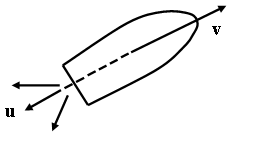
При движении ракеты ее масса уменьшается, так как запасенное в ней топливо сгорает, и продукты сгорания вылетают из соп-

Рис. 5.

ла в виде выхлопных газов.

Обозначим скорость ракеты в момент времени t через v, а массу через m. Пусть в этот момент времени начинают выходить выхлопные газы, скорость которых относительно ракеты равна u (рис. 4.). Через время dt масса ракеты уменьшится и станет равной m + dm, где –dm – масса вышедшего газа, а скорость увеличится и станет равной v + dv. Сравним теперь импульсы системы «ракета + выхлопные газы» в моменты времени t и t + dt. Первоначальный импульс равен, очевидно, mv. Импульс ракеты в момент времени t + dt будет (m + dm)(v + dv)¹, а импульс выхлопного газа будет –dm(v – u), так как скорость газа относительно Земли равна, очевидно, v – u. В соответствии с законом сохранения импульса мы должны приравнять величины импульсов в оба момента времени:

mv = (m + dm)(v + dv) – dm(v – u),

Откуда, пренебрегая (бесконечно малой второго порядка dmdv, находим

mdv + udm = 0, (5.7)

или

Будем считать, что скорость истечения газа не меняется с течением времени. Тогда последнее равенство можно переписать в виде

Откуда следует, что

где – постоянная интегрирования. Значение постоянной C определяется из условия, что в начале движения ракеты, т.е. при v = 0, масса ракеты равнялась начальному значению m₀: C = lnm₀. Подставляя это значение С в полученное соотношение, будем иметь

откуда окончательно получим

Эта формула определяет скорость ракеты в зависимости от изменения ее массы и носит название формулы Циолковского.

Формулу Циолковского часто записывают в виде

В такой форме она определяет начальную массу ракеты для сообщения ей скорости v. Если ракете, имеющей массу m, требуется сообщить скорость v, то начальная масса ракеты должна быть равна m₀. С увеличением расчетной скорости v начальная масса m₀ экспоненциально возрастает. При v >> u отношение m₀ / m получается очень большим. Это и создает основные технические трудности при построении космических ракет, достигающих скорости порядка 10 км/с. Увеличение скорости выхлопных газов позволяет значительно уменьшить стартовую массу и тем самым облегчает задачу конструкторов.

Разделив обе части равенства (5.7) получим

(5.8)

Величина определяет скорость изменения массы ракеты (ежесекундный расход выхлопных газов). Видим, что произведение имеет размерность силы; ее называют реактивной силой. Она возникает вследствие того, что частицам газа сообщается скорость u. Предположим, что частицы газа находятся в покое относительно ракеты. Затем некоторой силой F им сообщено ускорение относительно ракеты, вследствие чего они получают скорость u. Сила, противодействующая этой силе F, по третьему закону динамики приложена к ракете и направлена в сторону, противоположную скорости выброшенного газа: она и есть реактивная сила, двигающая ракету.

5.3. Закон сохранения момента импульса

Из уравнения моментов следует, что если момент силы, действующий на материальную точку равен нулю, то вектор момента ее импульса будет сохраняться: L = const. Момент силы будет равен нулю либо если сила F равна нулю, либо если линия ее действия проходит через точку, относительно которой определяется момент импульса. Последнее имеет место, если сила F – центральная. Покажем, что момент импульса замкнутой системы будет сохраняться и для системы материальных точек. Как и прежде, рассмотрим сначала систему, состоящую из двух точек. Запишем уравнение моментов для каждой из них:

Здесь L₁, M₁₂, M₁ и L₂, M₂₁, M₂ – моменты импульса и моменты внутренних и внешних сил, действующих на первую и вторую точки соответственно. Сложив эти уравнения, получим

где L = L₁ + L₂ – момент импульса системы, – суммарный момент внешних сил, действующий на точки системы. Если система замкнута, то = 0, и в этом случае скорость изменения момента импульса системы будет

По свойству изотропии пространства правая часть этого равенства равна нулю. Действительно, если рассматриваемую систему

Рис. 5.1

как целое повернуть на угол dφ (рис. 5.1), то в силу изотропии пространства ни в состоянии системы, ни в ее внутренних движениях ничего не изменится. Поэтому полная работа внутренних сил при указанном повороте должна быть равна нулю: где dl₁ и dl₂ – элементарные векторы перемещения точек 1 и 2 при повороте системы как целого на угол dφ.

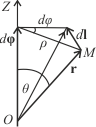
Элементарный угол поворота dφ будем считать вектором dφ, модуль которого равен самому углу dφ, а направление совпадает с осью (на рис. 5.1 c осью Z), вокруг которой происходит поворот так, что если смотреть навстречу этому вектору, будем видеть направление поворота против часовой стрелки (по правилу правого винта).

Найдем связь вектора перемещения dl с углом поворота dφ. Из рис. 5. 1 видно, что

(5.9)

Как видно из рис. 5.1, вектор dl перпендикулярен плоскости, содержащей векторы r и dφ, и образует с ними правовинтовую систему (правую тройку) векторов, поэтому равенство (5.9) представляет собой модуль векторного произведения

Это соотношение и определяет связь вектора перемещения с вектором угла поворота . С учетом этого получим

Левая часть этого равенства представляет собой сумму смешанных произведений трех векторов. Произведя циклическую перестановку этих векторов по формуле

,

будем иметь

Вследствие произвольности угла поворота δφ должно выполняться равенство M₁₂ + M₂₁ = 0. Тогда а значит, L = L₁ + + L₂ = const.

Обобщить закон сохранения момента импульса на системы с числом материальных точек, больших 2, можно аналогично тому, как это было сделано в случае закона сохранения импульса.

Если система не замкнута, то для момента импульса системы материальных точек будем иметь

где – векторная сумма всех внешних сил, действующих на систему.

С помощью этого соотношения можно получить и математическое выражение теоремы об изменении момента импульса системы:

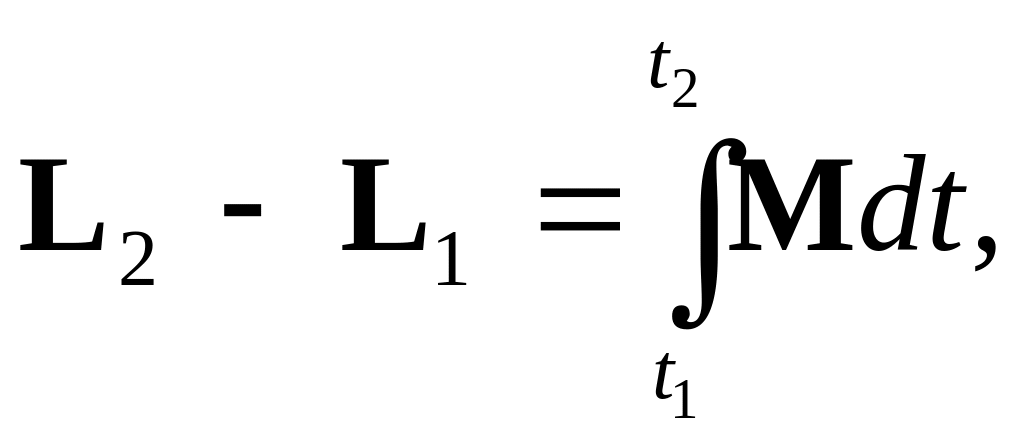
где L₁ и L₂ – моменты импульса системы в моменты времени t₁ и t₂ соответственно. Таким образом, изменение момента импульса системы материальных точек за промежуток времени от t₁ до t₂ равно импульсу момента силы за этот промежуток времени.

Аналогичным образом можно показать, что закон сохранения имеет место и для проекций вектора момента импульса на любую ось, проходящую через полюс: если вдоль какой-либо оси, например оси Z, момент силы M_z = 0, то соответствующая проекция момента импульса L_z = const.