Вопрос 5.

Общее уравнение прямой на плоскости. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Уравнение прямой, проходящей через две данные точки. Уравнение прямой в отрезках

1. В декартовой системе координат на плоскости каждая прямая определяется уравнением 1–й степени и, обратно, каждое уравнение 1–й степени определяет прямую.

Уравнение вида

Ax + By + C = 0 ( A² + B² ≠ 0 )

называется общим уравнением прямой.

Частные случаи:

• С=0; прямая проходит через начало координат.

• А=0; прямая параллельна оси ОХ

• В=0; прямая параллельна оси ОУ

Условие параллельности прямых:

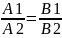
Условие перпендикулярности прямых (A1A2+B1B2=0)

2. Уравнение прямой с угловым коэффициентом

Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом

(b — ордината точки пересечения прямой с осью OY).

Угловым коэффициентом k прямой называется число k = tgα , где α — угол наклона прямой к оси OX (0 ≤ α < π).

Условие параллельности прямых: k₁ = k₂

Условие перпендикулярности прямых: k₁k₂ = −1

3. Уравнение прямой в отрезках

Уравнение прямой 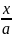+ 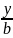= 1 называется уравнением прямой в отрезках

(a — абсцисса точки пересечения прямой с осью OX, b — ордината точки пересечения прямой с осью OY).

4. Уравнение прямой, проходящей через две точки

Уравнение прямой, проходящей через две точки M₁(x₁, y₁) и M₂(x₂, y₂), имеет вид :

=

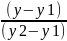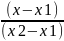
5. Угол между прямыми

Угол между прямыми с угловыми коэффициентами k1 и k2 определяется формулой:

=

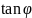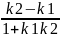
+ Если прямые заданы общими уравнениями, то тангенс угла между ними определяется по формуле: =

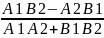
Вопрос 6

Общее уравнение плоскости. Уравнение плоскости, перпендикулярной данному вектору и проходящей через данную точку. Уравнение плоскости, проходящей через заданную точку и параллельной двум неколлинеарным векторам. Уравнение плоскости, проходящей через три заданные точки. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Уравнение плоскости в отрезках.

1. Общее уравнение плоскости.

Уравнение любой плоскости, перпендикулярной вектору 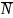{A,B,C}≠0, имеет вид:

Ax+By+Cz+D=0

(хотя бы одно из чисел A,B или C не равно нулю). Сам вектор наз. нормальным по отношению к этой плоскости.

2. Уравнение плоскости, проходящей через точку M перпендикулярно вектору N{A,B,C}:

A(x-x_M)+B(y-y_M)+C(z-z_M)=0.

3. Уравнение плоскости, проходящей через заданную точку M и параллельной двум неколлинеарным векторам

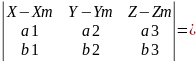0

4. Уравнение плоскости, проходящей через три заданные точки М, А, В:

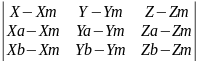= 0

5. Угол между двумя плоскостями.

Косинус угла между плоскостями равен модулю косинуса угла между нормалями к этим плоскостям:

=

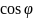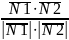
6. Условия параллельности и перпендикулярности двух плоскостей.

а) условие параллельности двух плоскостей:

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы   и   параллельны, а значит  .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

  или 

Условие перпендикулярности плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, следовательно,  или  .Т.е.  

7. Уравнение плоскости в отрезках. Плоскость отсекает на координатных осях "отрезки" x₁, y_1, z₁. Коэффициенты x₁, y_1, z₁ (≠ 0) определяют на координатных осях точки, через которые проходит плоскость:

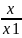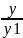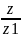+ + = 1