1.7 Предполные классы двоичных функций.

Определение:

Предполным классом К называется неполный класс, при добавлении любой функции , которая не принадлежит ему, получается класс полный.

Утверждение:

Предполный класс является замкнутым.

Доказательство: Допустим противное, что некоторый предполный класс К не замкнут: , тогда рассмотрим функцию

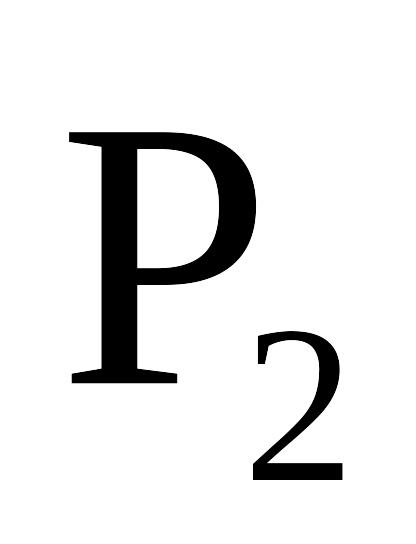
т.е. [ K,f ] не полный

Теорема:

В классе булевых функций есть ровно пять предполных классов : .

Доказательство :

В начале покажем, что данные классы являются предполными, а затем покажем, что других предполных классов нет.

1. Рассмотрим .

Данный класс содержит функции:

поэтому класс Т₀ не принадлехит классам Т₁, S, М, L.

Рассмотрим произвольную , тогда не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно класс является предполным.

2) Рассмотрим Т₁:

Рассмотрим произвольную не принадлежит ни одному из пяти классов, следовательно по теореме Поста является полной, следовательно предполный.

3) Рассмотрим S:

Рассмотрим не принадлежит ни одному из пяти классов Поста, следовательно по теореме Поста является полной, следовательно предполный .

4) Рассмотрим :

Рассмотрим не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно предполный.

5) Рассмотрим L:

Рассмотрим не принадлежит ни одному из пяти классов, следовательно по теореме Поста система полна, следовательно предполная. Все перечисленные классы не полны по теореме Поста.

Покажем, что других предполных классов в нет.

Допустим противное, что - предполный :

, следовательно в данном классе :

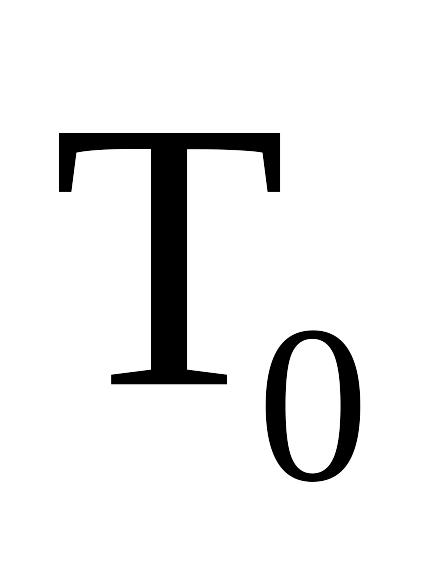
РИС.1

в силу того, что класс - предполный, следовательно включение на рис.1 невозможно, т.к. если бы было наоборот, то рассмотрим , мы бы получили, что все функции системы сохраняют 0, поэтому полной система не является, следовательно не является предполным.

По этой же причине в классе должна быть, , должна быть , должна быть , должна быть , следовательно из этих включений следует, что система является полной, противоречие с предполнотой этой системы.

Упражнения:

Найдите определяющие выражения функций через суперпозиции функций системы.

1)

2)

3)

4)

5)

Определение:

Полной системой бул. функций в замкнутом классе К является система функций, которая принадлежит данному классу, и замыкание которой совпадает с самим классом

.

Определение:

Базисом в замкнутом классе К называют систему В, которая полна в этом классе, но любая собственная подсистема полной в классе не является.

Пример 1: Рассмотрим множество всех булевых функций Р₂. В этом множестве рассмотрим систему .Эта система полна по т. Поста .

Чтобы определить,что все собственные подсистемы не полны, достаточно рассмотреть лишь максимальные по включению собственные подсистемы данной, получаемые из данной удалением какой-либо функции.

Если ни одна из этих подсистем не является полной, то полной не является и любая другая собственная подсистема (докажите предыдущие утвеждения)

В данном примере максимальные собственные подсистемы не полны, значит является базисом в Р₂.

Пример 2: Является ли система базисом в Р₂?

, поэтому система полна, но собственная подсистема также полна, поэтому данная система не базис в Р₂.

Определение:

Скажем, что функция f не зависима от системы , если эта функция не принадлежит замыканию системы : .

Пример 1: Рассмотрим функцию и систему :

Утверждаем, что не зависит от этой системы. Действительно, все функции системы являются линейными, поэтому в силу того, что суперпозиция линейных функций есть линейная функция, замыкание этой системы принадлежит классу линейных функций, а — функция не линейная. Поэтому не зависит от данной системы функций.

Пример 2: Рассмотрим функцию и систему :

x₁ x₂

0 0 1 0 0

0 1 1 1 1

1 0 0 1 1

1 1 1 1 1

Значит, зависима от функции .

Примечание: если функция не является независимой от системы, то будем называть ее зависимой от данной системы.

Утверждение:

Если система функций базис в замкнутом классе К , то тогда каждая функция базиса независима от оставшихся.

Доказательство:

Предположим противное: пусть существует базис в котором некоторая функция является зависимой от оставшихся. Для определенности будем считать, что это поэтому выражается через некоторые суперпозиции функций системы , но тогда система также является полной в классе К, поэтому не является базисом. Утверждение доказано.

Пример 1:

базис в Р₂

Упражнение: Докажите справедливость обратного утверждения: пусть полная система в К, и любая функция системы не зависит от оставшихся, тогда система – базис в К.

Полные системы в основных классах двоичных функций.

Утверждение 1:

Полной системой в классе Т₀ является система

Доказательство:

Обе функции принадлежат Т₀. Осталось показать, что , то есть любую можно представить суперпозицией функций

Рассмотрим и полином Жегалкина Тогда свободное слагаемое данного полинома равно 0 в силу того, что .Поэтому данный полином есть суперпозиция только . Это и есть требуемая суперпозиция.

Утвеждение 2:

В классе Т₁ полной является система .

Доказательство:

Рассмотрим . Покажем, что ее можно получить суперпозицией . В дальнейшем потребуются функции:

Рассмотрим функции (k+1 – число наборов, на которых f равна единице), которые получаются из по правилу:

для каждой функции оставляем соответствующий единичный набор, а на остальных (кроме 1…1) приравниваем к нулю.

Например:

0 0 0 0 0 0 0

0 0 1 0 0 0 0

0 1 0 1 1 0 0

0 1 1 0 0 0 0

1 0 0 1 0 1 0

1 0 1 1 0 0 1

1 1 0 0 0 0 0

1 1 1 1 1 1 1

В результате дополнительных функций будет столько, сколько единичных наборов без последнего. Очевидно

Поэтому, чтобы найти представление функции через достаточно найти представление каждой из добавочных функций через

Если f имеет один единичный набор, то это есть элементарная конъюнкция переменных без отрицания. В противном случае рассмотрим дополнительную функцию f_i . Не теряя общности будем считать, что соответствующий единичный набор имеет вид: . Тогда справедливо:

Например: f₁ равна 1 на наборах 010 и 111, поэтому

Утверждение 3:

В классе S полной является система

0 0 0 0 0

0 0 1 0 1

0 1 0 0 1

0 1 1 1 1

1 0 0 0 0

1 0 1 1 0

1 1 0 1 0

1 1 1 1 1

Все функции в данной системе являются самодвойственными. В дальнейшем потребуется - это самодвойственная фукция от 3-ех переменных, которая совпадает с логическим сложением на тех наборах, где первая переменная равна нулю (тогда на остальных наборах функция однозначно доопределяется по самодвойственности).

Самодвойственных функций, существенно зависящих от двух переменных нет:

0 0 01 0 1 1 0

0 1 01 0 1 0 1

1 0 10 1 0 1 0

1 1 10 1 0 0 1

Функции, не имеющие существенных переменных – константы, т.е. не самодвойственные функции от одной переменной есть .

коммутативные операции, относительно второй и третьей переменных при фиксированной первой:

и ассоциативны относительно второй и третьей переменных при фиксированной первой:

Будем обозначать:

Из этих двух свойств следует что значение выражения, в котором присутствуют символы не зависят от порядка расположения скобок в нем и расположения множителей.

Например:

Выражение, в котором присутствует символ на наборах, в которых равно 1, тогда и только тогда, когда все переменные выражения равны 1: =0 и

Значение выражения, в котором присутствует не зависит от расположения скобок и это выражение на наборах в которых равно 1, когда хотя бы одна из переменных равна 1.

Утверждение:

Например:

0 0 0 0

0 0 1 1

0 1 0 1

0 1 1 0

1 0 0 1

1 0 1 0

1 1 0 0

1 1 1 1

Доказательство:

Рассуждения в этом случае аналогичны случаю представления функции в виде СДНФ.Формальное доказательство следующее.

Заметим, что данное равенство достаточно показать только на первой половине наборов, где , тогда на оставшихся наборах равенство будет справедливо в силу самодвойственности функции в левой части и функции в правой части, как суперпозиция самодвойственных.

Рассмотрим набор

Покажем, что значение правой части на данных наборах равен 1 соответственно 0.

1) Рассмотрим слагаемые правой части, которые соответствуют набору .

Значение данного слагаемого на наборе равно , т.к. значение степени и основания совпадают, каждый множитель этого слагаемого равно 1, поэтому и все произведение равно1.

А поэтому значение всей дизъюнкции равно 1, т.к. существует слагаемое, равное 1.

2) . Рассмотрим произвольное слагаемое в правой части. Пусть оно соответствует единичному набору тогда наборы и различны, поэтому , тогда i-ый множитель на наборе будет равен 0, таким образом все слагаемые равны 0. Тогда значение всей правой части равно 0 на наборе . Утверждение доказано.

4) В классе монотонных функций полной является система .

Определение:

Нижней единицей монотонной функции называют набор значений переменных этой функции, на котором и для любого набора

Пример:

0 0 0 0

0 0 1 1

0 1 0 0

0 1 1 1

1 0 0 0

1 0 1 1

1 1 0 1

1 1 1 1

набор 001 для монотонной функции является нижней единицей набор 110 тоже нижняя единица функции .

Утверждение:

Пусть для монотонной функции : , . Тогда справедливо представление:

Иначе говоря, для каждой нижней единицы записывается конъюнкция переменных, которые равны 1 в данном наборе, затем берем логическую сумму полученных слагаемых.

В данном примере разложение следующее:

Доказательство:

1) тогда рассматриваем тот нижний набор, который меньше либо равен чем рассматриваемый , тогда в силу того, что в тех местах, где в наборе стоит 1, в также должна стоять 1.

Поэтому слагаемое, соответствующее набору равно 1 на наборе , а поэтому и вся дизъюнкция равна 1.

2)

Рассмотрим произвольное слагаемое, которое соответствует нижней единице , на наборе и покажем, что значение этого слагаемого равно 0 на наборе . Допустим противное, , что соответствующее слагаемое на наборе равно 1.Тогда в тех местах , где в наборе стоит 1 в наборе также стоит 1, то есть . Но в силу того, что получаем противоречие, т.к. значение , в то время как

5) В классе L полной системой является следующая .

Доказательство:

а это и есть все линейные функции.

Базисы в классах T₀ , T₁, S, M, L