Как найти угол между двумя векторами

Совет от Наталья Алтынбаева, автор КакПросто, добавлено 19 Август 2011

Угол между двумя векторами, выходящими из одной точки, это кратчайший угол, на который необходимо повернуть один из векторов вокруг своего начала до положения второго вектора. Определить градусную меру этого угла можно, если известны координаты векторов.

Начало формы

Конец формы

Инструкция

1Пусть на плоскости заданы два ненулевых вектора, отложенные от одной точки: вектор A с координатами (x1, y1) и вектор B с координатами (x2, y2). Угол между ними обозначен как θ. Чтобы найти градусную меру угла θ необходимо воспользоваться определением скалярного произведения.

2Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними, то есть (A,B)=|A|*|B|*cos(θ). Теперь нужно выразить из данной записи косинус угла: cos(θ)=(A,B)/(|A|*|B|).

3Скалярное произведение можно найти также по формуле (A,B)=x1*x2+y1*y2, так как скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов. Если скалярное произведение ненулевых векторов равно нулю, то векторы являются перпендикулярными (угол между ними равен 90 градусов) и дальнейшие вычисления можно не производить. Если скалярное произведение двух векторов положительно, то угол между этими векторами острый, а если отрицательно, то угол тупой.

4Теперь посчитайте длины векторов A и B по формулам: |A|=√(x1²+y1²), |B|=√(x2²+y2²). Длина вектора вычисляется как квадратный корень из суммы квадратов его координат.

5Найденные значения скалярного произведения и длин векторов подставьте в полученную в шаге 2 формулу для нахождения косинуса угла, то есть cos(θ)=(x1*x2+y1*y2)/(√(x1²+y1²)+√(x2²+y2²)). Теперь, зная значение косинуса, чтобы найти градусную меру угла между векторами нужно воспользоваться таблицей Брадиса или взять из этого выражения арккосинус: θ=arccos(cos(θ)).

6Если векторы A и B заданы в трехмерном пространстве и имеют координаты (x1, y1, z1) и (x2, y2, z2) соответственно, то при нахождении косинуса угла добавляется еще одна координата. В этом случае косинус угла равен: cos(θ)=(x1*x2+y1*y2+z1*z2)/(√(x1²+y1²+z1²)+√(x2²+y2²+z2²))

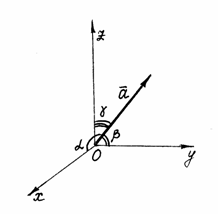
9)Направляющие косинусы вектора

Направление вектора в пространстве определяется углами  , которые вектор образует с осями координат (рис. 12). Косинусы этих углов называются направляющими косинусами вектора:  ,  ,  .   Рис. 12 Из свойств проекций: ,  ,  . Следовательно, ,  ,  .                                       (2.5) Легко показать, что 1)      ; 2)     координаты любого единичного вектора совпадают с его направляющими косинусами:  .

10) Определение векторного произведения

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

      

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. са и сb;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют п равую тройку.

Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j.  Докажем, например, что iхj=k.

1) ki, kj;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).

Свойства векторного произведения

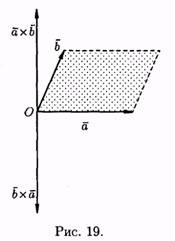
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).

 Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxa противоположной ориентации). Стало быть axb = -(bxa ).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. (а хb ) = (а ) х b = а х (b ).

Пусть >0. Вектор (ахb ) перпендикулярен векторам а и b . Вектор ( а)хb также перпендикулярен векторам а и b (векторы а, а лежат в одной плоскости). Значит, векторы (ахb ) и ( а)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому (a хb )= ахb . Аналогично доказывается при <0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.

В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) хс= ахс+b хс.

Примем без доказательства.

11)

Смешанное произведение векторов и его свойства

Смешанным произведением векторов   называется число  , равное скалярному произведению вектора   на векторное произведение векторов   и  . Смешанное произведение обозначается  .

Геометрические свойства смешанного произведения

1. Модуль смешанного произведения некомпланарных векторов   равен объему   параллелепипеда, построенного на этих векторах. Произведение   положительно, если тройка векторов   — правая, и отрицательно, если тройка   — левая, и наоборот.

2. Смешанное произведение   равно нулю тогда и только тогда, когда векторы   компланарны:

 векторы   компланарны.

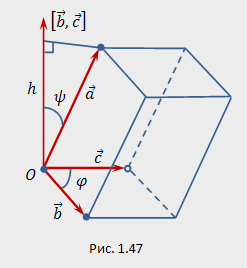
Докажем первое свойство. Найдем по определению смешанное произведение:  , где   — угол между векторами   и  . Модуль векторного произведения (по геометрическому свойству 1) равен площади   параллелограмма, построенного на векторах   и  : . Поэтому  . Алгебраическое значение   длины проекции вектора   на ось, задаваемую вектором  , равно по модулю высоте   параллелепипеда, построенного на векторах   (рис. 1.47). Поэтому модуль смешанного произведения равен объему   этого параллелепипеда:

Знак смешанного произведения определяется знаком косинуса угла  . Если тройка   правая, то   и смешанное произведение   положительно. Если же тройка   левая, то   и смешанное произведение   отрицательно.

Докажем второе свойство. Равенство   возможно в трех случаях:   или   (т.е.  ),или   (т.е. вектор   принадлежит плоскости векторов   и  ). В каждом случае векторы   компланарны (см. разд. 1.1)

Алгебраические свойства смешанного произведения

1. При перестановке двух множителей смешанное произведение изменяет знак на противоположный:

При циклической (круговой) перестановке множителей смешанное произведение не изменяется:

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из геометрического свойства 1 и свойств ориентации троек векторов (см. разд. 1.9), поскольку от перестановки двух множителей модуль смешанного произведения не изменяется, а меняется только ориентация тройки. При циклической перестановке векторов ориентация тройки не изменяется.

Второе свойство следует из линейности скалярного произведения и свойства 1

Пример 1.21. Объем параллелепипеда, построенного на векторах  , равен  . Найти объем параллелепипеда, построенного на векторах .

Решение. Используя алгебраические и геометрические свойства, найдем смешанное произведение а затем его модуль  . По первому геометрическому свойству смешанного произведения искомый объем равен  .

Теорема 1.9 (формула вычисления смешанного произведения). Если векторы   в правом ортонормированном базисе   имеют координаты  ;  ;   соответственно, то смешанное произведение этих векторов находится по формуле

В самом деле, учитывая (1.10) и (1.15), по определению находим: что и требовалось доказать.

12) Общее уравнение прямой на плоскости. Рассмотрим уравнение прямой с угловым коэффициентом  . Перенесем все слагаемые в левую часть и перепишем его в следующем виде:

,

              -                                         (3.6)общее уравнение прямой, где  и  не равны нулю одновременно, т.е.  .

Рассмотрим частные случаи уравнения (3.6).

1)Пусть  . Тогда уравнение   можно записать в виде:  . Обозначим  .

Если  ,  , то получим  (уравнение прямой с угловым коэффициентом);

Если  ,  , то  (уравнение прямой, проходящей через начало координат);

Если  ,  , то   (уравнение прямой, параллельной оси Оу);

Если  ,  , то   (уравнение оси Ох).

3)      Пусть  ,  . Тогда уравнение   примет вид  . Обозначим  .

Если  , то получим   (уравнение прямой, параллельной оси Оу);

Если  , то   (уравнение оси Оу).

Т.о., при любых значениях коэффициентов  ,  (не равных одновременно нулю) и  уравнение   есть уравнение некоторой прямой линии на плоскости Оху.

- общее уравнение прямой.

13) Уравнение прямой с угловым коэффициентом.

Пусть дана прямая L на координатной плоскости Оху.

Определение. Углом наклона прямой к оси абсцисс называется уголповорота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.

  

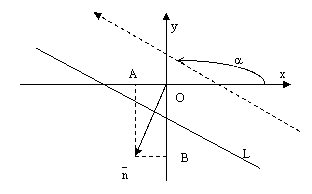
                                              рис.1.

Из определения следует, что угол наклона   прямой L к оси Ох может изменяться от нуля до  :  . Если прямая  , то  .

   Пусть

                                                                      (1)

– общее уравнение прямой L, где   – нормальный вектор прямой L и  . Тогда   и   (см. рис.1). Выразим у изуравнения (1)

                                     .

                                   ,  .

Уравнение прямой L принимает вид:

                                             .

Определение. Уравнение прямой вида

                                                                              (2)

называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.

Теорема. В уравнении прямой с угловым коэффициентом

                                            

угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:

                                                .                                (3)

   Доказательство. 1) Если прямая  , то   и  . С другой стороны, ее нормальный вектор   и  .

   Тогда   и, следовательно,  , ч.т.д.

2) Пусть  , тогда  ,   и  . Пусть F – точка пересечения прямой L с осью абсцисс. Тогда

                                     ,  .

Опишем окружность единичного радиуса с центром в точке F , а в точке оси Ох с координатой   проведем касательную m к этой окружности. См. рис.2.

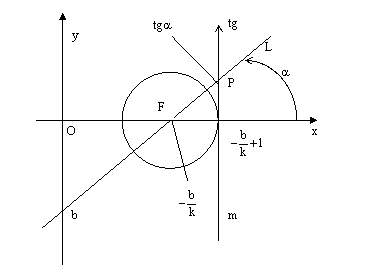
                                                рис.2.

Выберем положительное направление на прямой m, так, чтобы  . Тогда ось m является осью тангенсов для данной единичной (тригонометрической) окружности.

   Пусть Р – точка пересечения прямой L с осью тангенсов m. Тогда, с одной стороны,  , где   – угол наклона прямой L к оси Ох, а, с другой стороны, точка   и  , откуда и следует равенство  , ч.т.д.

Теорема доказана.

   Заметим, что приведенное доказательство принадлежит автору этих лекций. Достоинством этого доказательства является то, что оно не зависит ни от величины угла наклона  , ни от величины коэффициента  .

   В заключение отметим, что коэффициент b в уравнении (2) равен величине отрезка, отсекаемого прямой от оси ординат (см. рис.2).

Угловой коэффициент в уравнении прямой. Геометрический смысл коэффициента.

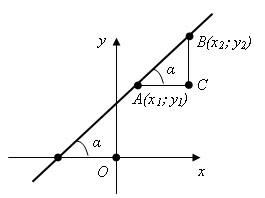
Преобразуем уравнение прямой ax + by + c=0 к виду    Введем обозначения    Тогда получим y = kx + l.    Возьмем две точки на прямой A (x1; y1) и B (x2; y2), такие что x1 < x2.  Их координаты удовлетворяют уравнению прямой:    Вычитая эти равенства почленно, получим    Проведя прямую через точку A параллельно оси x и прямую через точку B параллельную оси y, мы получим треугольник ABC. 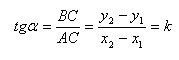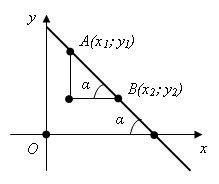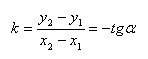Замечаем, что    Если прямая расположена следующим образом :    То    Таким образом, коэффициент k в уравнении прямой с точностью до знака равен тангенсу острого угла, который образует прямая с осью x.  Коэффициент k в уравнении прямой называется угловым коэффициентом прямой.