Определение смешанного произведения.

Смешанное произведение определяется для трех векторов, заданных в трехмерном пространстве.

Определение.

Смешанным произведением трех векторов и называется действительное число, равное скалярному произведению векторов и , где - векторное произведение векторов и .

Из определения понятно, почему смешанное произведение часто называют векторно-скалярным произведением.

Смешанное произведение векторов и обычно обозначают . В таких обозначениях по определению смешанного произведения .

Смешанное произведение в координатной форме.

Покажем, как находится смешанное произведение, если известны координаты умножаемых векторов в прямоугольной системе координат. Пусть - координатные векторы.

Векторное произведение в координатах имеет вид   а скалярное произведение векторов в прямоугольной системе координат равно сумме произведений соответствующих координат, поэтому,

Таким образом, смешанное произведение векторов равно определителю матрицы третьего порядка, строками которой являются координаты умножаемых векторов, то есть, .

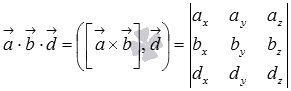Свойства смешанного произведения.

Из свойств векторного произведения и свойств скалярного произведения следуют следующиесвойства смешанного произведения:

1. ;

2. ;

3. 

Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.

Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.

Действительно, если , то по определению векторного произведения , следовательно, смешанное произведение равно нулю, так как . Если же или , то угол между векторами и равен , следовательно, по определению скалярного произведения векторов .

Свойства смешанного произведения обычно применяются при доказательстве тождеств или неравенств.

Рассмотрим несколько характерных задач.

Пример.

Докажите равенство , где - некоторое действительное число.

Решение.

Преобразуем левую часть равенства, обратившись к третьему свойству смешанного произведения:

Выше мы показали, что 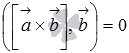, следовательно,

По первому свойству смешанного произведения , а . Таким образом, .

Поэтому,

Что и требовалось доказать.

Пример.

Докажите, что модуль смешанного произведения трех векторов не превосходит произведения длин этих векторов.

Решение.

Иными словами, нам требуется доказать неравенство .

По определению скалярного и векторного произведения векторов, мы можем записать

Из свойств основных элементарных функций мы знаем, что . Следовательно, что и требовалось доказать.

К началу страницы

Вычисление смешанного произведения, примеры и решения.

Проще всего смешанное произведение находится, когда известны координаты векторов. Для вычисления используется формула .

Пример.

Даны координаты трех векторов в прямоугольной системе координат . Найдите смешанное произведение .

Решение.

Мы выяснили, что смешанное произведение векторов может быть вычислено через определитель матрицы третьего порядка, строками которой являются координаты векторов, то есть,

Ответ:

.

Пример.

Найдите векторно-скалярное произведение векторов , где - орты прямоугольной декартовой системы координат.

Решение.

Данные векторы имеют следующие координаты (при необходимости смотрите статьюкоординаты вектора в прямоугольной системе координат)

Осталось воспользоваться формулой для вычисления смешанного произведения через координаты векторов

Ответ:

.

Смешанное произведение векторов также может быть вычислено, если известны длины векторов и углы между ними. Рассмотрим решение характерного примера.

Пример.

В правой прямоугольной декартовой системе координат заданы три взаимно перпендикулярных вектора и , образующих правую тройку, их длины равны соответственно 4, 2 и 3. Найдите их смешанное произведение .

Решение.

Обозначим .

Нам известно, что скалярное произведение векторов равно произведению их длин на косинус угла между ними, поэтому .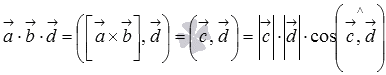

Сразу подставим значение длины вектора , известное из условия: .

У нас остались неизвестные и . Найдем их.

По условию 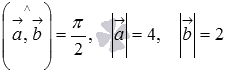, тогда по определению векторного произведения находим длину вектора :

Из определения векторного произведения мы можем заключить, что вектор перпендикулярен вектору и вектору , причем тройка векторов будет правой, так как векторы и заданы в правой прямоугольной декартовой системе координат. Следовательно, векторы и будут сонаправленными, то есть, .

Подставляем полученные результаты и получаем искомое смешанное произведение: .

Ответ: