Нахождение нод отрицательных чисел

Если одно, несколько или все числа, наибольший делитель которых нужно найти, являются отрицательными числами, то их НОД равен наибольшему общему делителю модулей этих чисел. Это связано с тем, что противоположные числа a и −a имеют одинаковые делители, о чем мы говорили при изучении свойств делимости.

Пример.

Найдите НОД отрицательных целых чисел −231 и −140.

Решение.

Модуль числа −231 равен 231, а модуль числа −140 равен 140, иНОД(−231, −140)=НОД(231, 140). Алгоритм Евклида дает нам следующие равенства:231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Следовательно,НОД(231, 140)=7. Тогда искомый наибольший общий делитель отрицательных чисел−231 и −140 равен 7.

Ответ:

НОД(−231, −140)=7.

Пример.

Определите НОД трех чисел −585, 81 и −189.

Решение.

При нахождении наибольшего общего делителя отрицательные числа можно заменить их абсолютными величинами, то есть, НОД(−585, 81, −189)=НОД(585, 81, 189). Разложения чисел 585, 81 и 189 на простые множители имеют соответственно вид585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими простыми множителями этих трех чисел являются 3 и 3. Тогда НОД(585, 81, 189)=3·3=9, следовательно,НОД(−585, 81, −189)=9.

Ответ:

НОД(−585, 81, −189)=9.

35. Корені многочлена. Теорема Безу. (33 и выше)

36. Кратні корені, критерій кратності кореня.

Кратные корни многочленов

 

Определение 1. Если в разложении многочлена -степени

,

некоторые множители окажутся одинаковыми, то

,

то -называется корнем кратности,-кратностии т.д.

 

 Теорема 1. Если а является корнем многочлена кратности, то для производнойэто число является корнем кратности.

Доказательство. Пусть

,

где не обращается в 0 при.

,

т.е. является корнем кратности.

Следствие. Число а является корнем кратности для,…, корнем кратности 1 для.

37. Відділення кратних коренів.

Метод Штурма отделения корней многочлена

Рассмотрим пример отделения корней многочлена по методу Штурма на примере многочлена. Для применения этого метода к многочлену требуется составить систему Штурма . Замечание: многочлен должен иметь действительные коэффициенты и не иметь кратных корней. Правило построение системы Штурма: 1) 2) Если известны и , то будет равен остатку от деления на , взятым с обратным знаком: . Замечание: В процессе деления, в отличии от алгоритма Евклида, остаток можно умножать лишь на произвольное положительное число (для того, чтобы коэффициент при старшей степени был целым или просто удобным), т.к. знак остатка принципиально важен. Составим систему Штурма для заданного многочлена 1)  2) Умножаем остаток на 4 и берем его с противоположным знаком. Получим  3) Домножим на 25, поменяем знак и получим:  4) Домножим остаток на обратную величину, поменяем знак и получим:  Получили систему Штурма: Определим знаки этих многочленов при и при . Конечно, вычислять тут ничего не нужно, достаточно посмотреть только на коэффициенты при старших степенях и на сами эти степени. Например: И т.д. Занесем результаты выводов в таблицу:

						Кол-во перемен знаков
	+	-	+	-	+	4
	+	+	+	+	+	0

Вывод: Многочлен имеет ровно действительных корня. Локализуем их. Для этого продолжим таблицы, выбрав «на глазок» точки для проверки знаков многочленов системы. Первую точку нужно взять такой, чтобы набор плюсов и минусов был одинаков с , а последующие выгодны такие, при которых количество перемен знаков изменяется, причем таких перемен должно быть ровно столько, сколько корней имеет многочлен.

						Кол-во перемен знаков
	+	-	+	-	+	4
	0	+	-	-	+	2

Замечание: повезло, т.к. при получаем , т.е. — корень многочлена. Мы не только локализовали, но определили его точное значение. Заметим, что количество перемен знаков уменьшается на 2, т.е. на этом интервале есть один корень, он дает одно изменение, и корень в этой точке дает еще одну перемену. Но продолжим.

						Кол-во перемен знаков
	+	-	-	-	+	2
	-	-	-	+	+	1
	-	-	+	+	+	1
	+	+	+	+	+	0

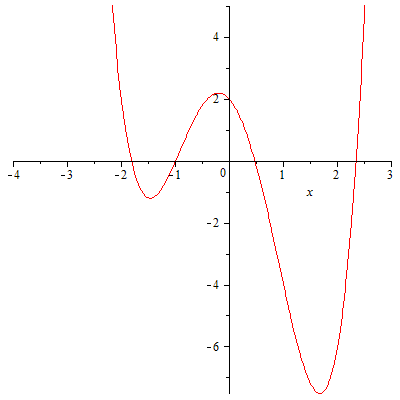
Вывод: Про корни можно сказать:  При помощи компьютерных технологий можно построить график функции и убедиться в правильности рассуждений.

38. Розклад многочлена по степенях .