Питання для контролю вивченого матеріалу

1. Дайте означення похідної.

2. Яка функція називається диференційованою в точці та на відрізку?

3. Сформулюйте залежність між неперервністю та диференційованістю функції.

4. Який геометричний зміст похідної?

5. В чому полягає механічний зміст похідної?

6. Як знайти миттєву швидкість прямолінійного нерівномірного руху?

7. Як обчислити кутовий коефіцієнт дотичної до кривої в даній точці?

8. Який вигляд мають рівняння дотичної та нормалі до кривої?

Література

1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2 изд., перераб. и доп. – М.: Наука, 1990 – 576с. : ил.

2. Соколенко О.І. Вища математика. – К.: Видавничий центр „Академія”, 2002. – 431с.

3. Лисичкин В.Т., Соловейчик И.Л. Математика: Учебное пособие для техникумов. – М.: Вища школа, 1991. – 480с.: ил.

4. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум. – К.: Вища школа, 1991. – 407с. : іл.

Тема 2: Складена функція та її похідна.

1. Поняття складеної функції.

2. Похідна складеної функції.

Короткі теоретичні відомості

Означення. Функція, яка задається у вигляді , називається складеною функцією, складеною із функцій та .

Складену функцію часто записують у вигляді , де .

При цьому аргумент називається незалежною змінною, а - проміжним аргументом.

Нехай задано складену функцію , де .

Теорема. Якщо функція диференційована в деякій точці , а функція визначена на множині значень функції та диференційована в точці , то складена функція в даній точці має похідну, яка знаходиться за формулою

(1).

Приклад. Знайти похідну функції .

° Ця функція є складеною степеневою функцією, а саме 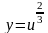, де . Тому

. •

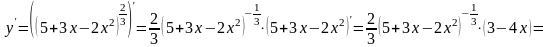
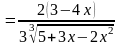Питання для контролю вивченого матеріалу

1. Яка функція називається складною?

2. Як знайти похідну складної функції?

3. Продиференціювати функцію .

Література

1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 576 с.: ил.

2. Лисичкин В.Т., Соловейчик И.Л. Математика: Учебное пособие для техникумов. – М.: Высш. шк., 1991. – 480 с.: ил.

3. Дюженкова Л.І., Носаль Т.В.: Вища математика: Практикум. – К.: Вища школа, 1991. – 407 с.: іл.

4. Соколенко О.І. Вища математика. – К.: Видавничий центр „Академія”. 2002, - 431с.

Тема 3: Похідні і диференціали вищих порядків.

1. Поняття похідних вищих порядків.

2. Поняття диференціалів вищих порядків.

Короткі теоретичні відомості.

1. Якщо функція диференційована, то її похідна 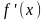є функцією x. Якщо ця функція диференційована, то її похідна називається другою похідною, або похідною другого порядку функції , і позначається або :

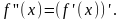
При цьому називається першою похідною або похідною першого порядку функції .

Похідна другої похідної функції називається третьою похідною або похідною третього порядку даної функції і позначається 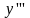або :

Похідною n-го порядку функції називається перша похідна похідної (n-1)-го порядку даної функції і позначається 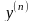або :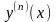

Похідна порядку вище першого називається похідною вищого порядку.

Приклад 1.

Знайти похідну 4-го порядку функції:

а)

б)

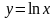
Розв’язання.

1)Знайдемо послідовно 1,2,3 і 4-у похідні:

а)

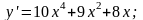
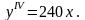
б)

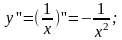
Приклад 2.

Знайти похідну n-го порядку функції

Розв’язання.

1) Знайдемо послідовно 1,2,3 похідні:

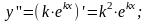
2) По аналогії знаходимо:

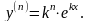
2. Диференціал від диференціала даної функції називається її другим диференціалом (або диференціалом другого порядку) і позначається 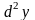і

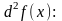
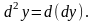
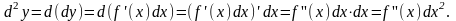
Аналогічно вводяться поняття диференціалів 3,4-го порядку і т.і.

Взагалі, п-м диференціалом (або диференціалом n-го порядку) функції називається диференціал від її (n-1)-го диференціала.

Диференціал n-го порядку функції позначається або

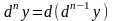
Приклад 3.

Знайти диференціал 4-го порядку функції

Розв’язання.

Знайдемо послідовно 1,2,3,4-й диференціали функції:

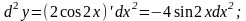
Питання для контролю вивченого матеріалу.

1. Що називається другою похідною?

2. Що називається третьою похідною?

3. Що називається n-ою похідною?

4. Що називається похідною вищого порядку?

5. Що називається другим диференціалом функції?

6. Що називається п-м диференціалом функції?

7. Знайти третю похідну функції

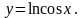
8. Знайти другий диференціал функції .
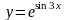