Питання для контролю вивченого матеріалу

1. Я

   к прочитати запис ? Дайте означення границі функції в точці.

2. Д

   айте означення границі функції на нескінченності. Поясніть основний прийом розкриття невизначеності на прикладі .

3. Сформулюйте та запишіть першу та другу чудові границі.

Література

1.Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие.-2-изд., перераб. и дополненное – М.: Наука, 1990 – 576с.

2.Соколенко О.І. Вища математика. – К. : Видавничий центр „Академія”, 2002 – 431с.

3.Лисичкин В.Т., Соловейчик М.Л. Математика: учебное пособие для техникумов. – М.: Вища школа, 1991. – 480с.: ил.

4.Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум. –К.: Вища школа, 1991 – 407с.: іл.

Тема 2: Точки розриву. Асимптоти.

1. Неперервність функції. Точки розриву.

2. Асимптоти.

Короткі теоретичні відомості

Функція f називається неперервною в точці х_0, якщо , тобто якщо виконуються умови: а); ;б)існує скінчена границя в точці х₀; в) ця границя дорівнює значенню функції в точці х₀.

При порушенні хоча б однієї з цих умов функція називається розривною в точці ,а сама ця точка називається точкою розриву.

Точка х₀ називається точкою розриву першого роду, якщо в ній існують скінчені односторонні границі

та , а якщо хоч одна з границь є нескінченою або взагалі не існує, то - другого роду.

Пряма називається асимптотою кривої або графіка функції y=f(x), якщо відстань від точки М(x;f(x))кривої до цієї прямої прямує до нуля при віддаленні точки М в нескінченність.

Якщо , то пряма х=х₀ називається вертикальною асимптотою кривої y=f(x). При цьому розглянута границя може бути односторонньою, а під символом слід розуміти + або - .

Якщо , то пряма називається похилою асимптотою кривої . При цьому якщо k=0, то асимптота називається горизонтальною.

Числа k і b обчислюють за формулами

(1)

При цьому вказані границі можуть бути різними, при (для правої похилої асимптоти)і при (для лівої похилої асимптоти).

Приклад. Знайти асимптоти кривої .

Оскільки , то х=4 є вертикальною асимптотою.

Знайдемо похилу асимптоту. Користуючись формулами (1), дістанемо

Отже, пряма y=2x+8 є похилою асимптотою.

Питання для контролю вивченого матеріалу

1. Дайте означення неперервної функції.

2. Що таке точка розриву? Які вони бувають?

3. Що називається асимптотою кривої?

4. Які бувають асимптоти та як вони знаходяться?

5. Знайти асимптоти кривої .

Література

1. Валуцэ И.И., Дилигул Г.Д., Математика для техникумов на базе средней школы: Учеб. пособие 2-е изд., перераб. и доп.-М.:Наука,1990-576с.:ил.

2. Соколенко О.И Вища математика: Підручник -К.: Видавничий центр „Академія”,2002-432с.

3. Дюженкова Л.І.Носаль Т.В. Вища математика: Практикум: Навч. посібник.-К.: Вища шк.,1991-407с.:іл.

Розділ 4. Диференціальне числення функції однієї змінної

Тема 1: Геометричний і фізичний зміст похідної. Рівняння дотичної та нормалі до графіка функції.

1. Похідна функції.

2. Геометричний зміст похідної.

3. Фізичний (механічний) зміст похідної.

4. Рівняння дотичної та нормалі до кривої.

Короткі теоретичні відомості

Нехай функція f(x) визначена в деякому околі точки х₀

Означення 1. Похідною функції f(x) в точці х₀ називається границя відношення приросту функції f(x₀ ) до приросту аргументу х при х→0, якщо ця границя існує, і позначається .

Отже, = (1)

Означення 2. Операція знаходження похідної називається диференціюванням функції.

Означення 3. Функція, яка має похідну в точці х₀ , називається диференційованою в цій точці. Функція, яка має похідну в кожній точці інтервалу (а;в), називається диференційованою на цьому інтервалі.

Теорема 1. Якщо функція f(x) диференційовна в точці х₀ , то вона неперервна в цій точці.

М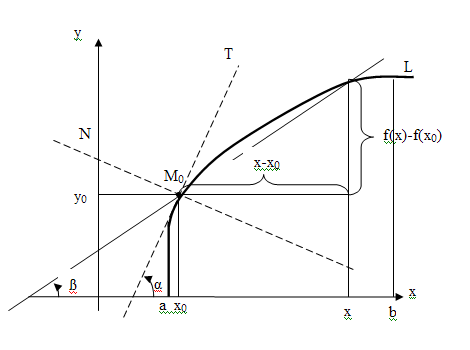 ал. 1

Означення 4. Дотичною до кривої L в точці називається граничне положення січної М₀М ( якщо таке граничне положення існує).

Геометричний зміст похідної: Похідна функції f(x) в точці х₀ дорівнює кутовому коефіцієнту дотичної, проведеної до графіка даної функції в його точці у абсцисою х₀.

Якщо S=S(t) – функція, що описує закон руху матеріальної точки, то миттєва швидкість v в момент часу t дорівнює похідній, шляху за часом (механічний зміст похідної), тобто . Прискорення а є похідною швидкості за часом, тобто .

Рівняння дотичної до кривої L в точці (x₀,f(x₀)) запишемо як рівняння прямої, що проходить через точку (х₀ ,f(x₀)) та має кутовий коефіцієнт , тобто

(2)

Означення 5. Пряма М₀N, перпендикулярна дотичній М₀Т в точці М₀, називається нормаллю до кривої L в точці М₀ (див. мал. 3).

Так як кутовий коефіцієнт нормалі дорівнює , то рівняння нормалі до кривої L в точці (х₀;f(x₀)) має вигляд.

(3)

Приклад: Скласти рівняння дотичної і нормалі до кривої в її точці з абсцисою х₀=2.

Знаходимо ,

Підставивши знайдені значення та в рівняння (2) та (3), знайдемо шукані рівняння дотичної , або та нормалі , або .